协会类网站免费模板wordpress邮件重置密码
背景:win10 下载docker时需要wsl2,下了个微软商店的Ubuntu 。写这篇文章的原因是当时查了资料ubuntu的问题和微软下载的Ubuntu还是有一些区别,问题不好解决,故写此文。
问题:用命令ifconfig eth0 down后再执行ifconfig eth0 up,ping外网失败,
报错:Temporary failure in name resolution

分析:经过查资料,发现网关被删除。可以用route -n 查询
没有网关的截图:

有网关的截图:

解决办法:sudo route add default gw 172.21.16.1
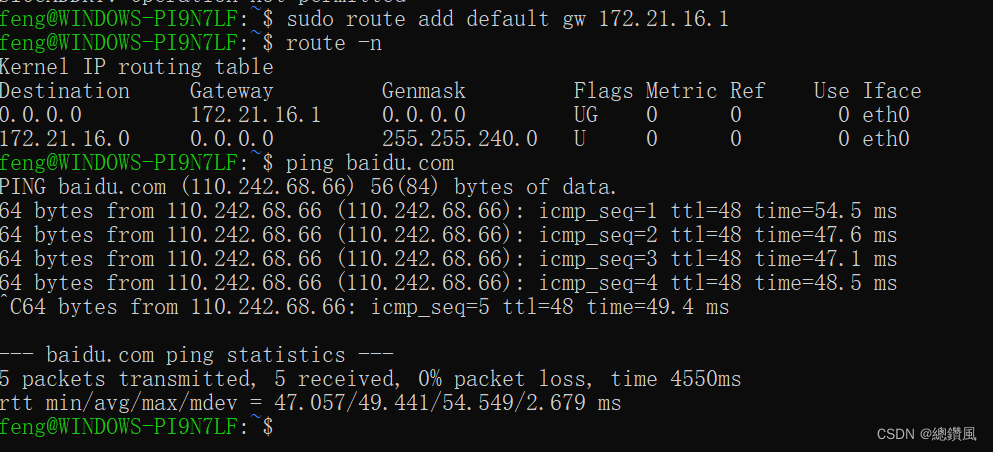
成功!
