网站应用软件怎么架设数据可视化
文章目录
- 背景
- QXmlStreamReader简单介绍
- 使用QXmlStreamReader
- 添加头文件<QXmlStreamReader>
- toString()
- toInt()
- 完整代码
背景
项目中遇到需要解析某个方法返回的xml字符串,奈何C/C++中没有原生的方法可供调用,只能使用第三方库,搜了一圈资料发现都不好用。刚好项目中用的Qt,瞬间想到了Qt中提供的各种各样的函数,去仔细查了一下Qt中提供的函数——QXmlStreamReader,真救命稻草,几行代码就搞定了我的需求。
QXmlStreamReader简单介绍
自QT4.3版本开始,QT提供了两个新类来读写XML:QXmlStreamReader 和 QXmlStreamWriter。顾名思义,QXmlStreamReader用于读取XML,QXmlStreamWriter用于写入XML。这两个类都使用流的方式操作xml,比起使用DOM和SAX解析xml,这是最快最方便的操作xml的方法。
使用QXmlStreamReader
添加头文件
假设有如下xml字符串,解析获取其中name、attr1、attr2的值
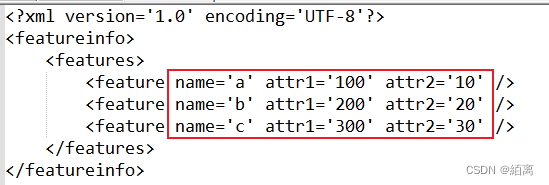
使用QXmlStreamReader只需要简单的几行代码就能搞定
QString xml = R"(<?xml version='1.0' encoding='UTF-8'?><featureinfo><features><feature name='a' attr1='100' attr2='10' /><feature name='b' attr1='200' attr2='20' /><feature name='c' attr1='300' attr2='30' /></features></featureinfo>)";// 1、初始化QXmlStreamReaderQXmlStreamReader reader(xml);while(!reader.atEnd() && !reader.hasError()) {// 2、使用readNext读取下一行QXmlStreamReader::TokenType token = reader.readNext();if (token == QXmlStreamReader::StartElement) { // 判断是否为xml开始标签,即左边的<if (reader.name() == "feature") { // 标签名称qDebug() << "name:" << reader.attributes().value("name").toString() << " attr1:" << reader.attributes().value("attr1").toInt() << " attr2:" << reader.attributes().value("attr2").toInt();}}}
最后调用attributes()方法获取对应的属性值即可。需要注意的是,reader.attributes().value(“name”).toString()还是toInt(),需要根据实际数据类型来确定,字符串就选toString,整数就选toInt。区别如下:
toString()
qDebug() << "name:" << reader.attributes().value("name").toString() << " attr1:" << reader.attributes().value("attr1").toString() << " attr2:" << reader.attributes().value("attr2").toString();
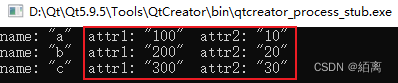
可以看到输出的也是字符串类型。
toInt()
qDebug() << "name:" << reader.attributes().value("name").toString() << " attr1:" << reader.attributes().value("attr1").toInt() << " attr2:" << reader.attributes().value("attr2").toInt();
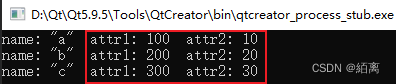
此处输出的是int类型。
完整代码
项目文件test.pro
TEMPLATE = app
CONFIG += console c++11
CONFIG -= app_bundle
SOURCES += main.cpp
main.cpp
#include <iostream>
#include <QString>
#include <QXmlStreamReader>
#include <qDebug>using namespace std;int main()
{QString xml = R"(<?xml version='1.0' encoding='UTF-8'?><featureinfo><features><feature name='a' attr1='100' attr2='10' /><feature name='b' attr1='200' attr2='20' /><feature name='c' attr1='300' attr2='30' /></features></featureinfo>)";// 1、初始化QXmlStreamReaderQXmlStreamReader reader(xml);while(!reader.atEnd() && !reader.hasError()) {// 2、使用readNext读取下一行QXmlStreamReader::TokenType token = reader.readNext();if (token == QXmlStreamReader::StartElement) { // 判断是否为xml开始标签,即左边的<if (reader.name() == "feature") { // 标签名称qDebug() << "name:" << reader.attributes().value("name").toString() << " attr1:" << reader.attributes().value("attr1").toInt() << " attr2:" << reader.attributes().value("attr2").toInt();//qDebug() << "name:" << reader.attributes().value("name").toString() << " attr1:" << reader.attributes().value("attr1").toString() << " attr2:" << reader.attributes().value("attr2").toString();}}}return 0;
}
