做网站费用怎么付18款禁用软件app破解版
🚀前言
本期是一篇关于顺序结构的题目的复盘,通过复盘基础知识,进而把基础知识学习牢固!通过例题而进行复习基础知识。
 🚩目录
🚩目录
前言
1.字符三角形
分析:
知识点:
代码如下
2. 字母转换
题目分析:
知识点:
代码如下
3. 再分肥宅水
题目分析:
知识点:
代码如下
4. 数字反转
题目分析:
知识点:
代码如下
总结
🍊1.字符三角形
题目描述
给定一个字符,用它构造一个底边长 5 个字符,高 3个字符的等腰字符三角形。
输入格式
输入只有一行,包含一个字符。
输出格式
该字符构成的等腰三角形,底边长 5 个字符,高 3 个字符。
输入输出样例
输入 #
*输出 #1复制
**** *****说明/提示
对于 100%100% 的数据,输入的字符是 ASCII 中的可见字符。
分析:
- 根据题目的描述可以得知,本题目主要考察的是关于循环的问题,只需要输入制定字符,然后输入的3行5列的等腰三角形这个是固定的。
-
这里需要注意的是Scanner扫描器没有获取char类型的方法,可以使用Scanner.next()进行获取字符串,然后通过String类下的CharAt方法进行截取或则subString()。
-
第一行是一个字符,第二行是三个,第三行是五个可以找到规律2*i(i是从1开始)-1。
知识点:
CharAt()函数进行截取字符串。
char charAt(int index)
返回
char指定索引处的值。 指数范围为0至length() - 1。 该序列的第一个char值在索引0,下一个索引为1,依此类推,与数组索引一样。
代码如下
Scanner sc = new Scanner(System.in);
// 1.这里需要注意的是Scanner扫描器没有获取char类型的方法,
// 可以使用Scanner.next()进行获取字符串,
// 然后通过String类下的CharAt方法进行截取或则subString()char s=sc.next().charAt(0);
// for (int i = 0; i < 3; i++) {
// 输出空格for (int j = 0; j <3-i-1; j++)System.out.print(" ");
// 负责输出指定字符串for (int k=0;k<(i+1)*2-1;k++){System.out.print(s);}
// 整体换行System.out.println();}🌽2. 字母转换
题目描述
输入一个小写字母,输出其对应的大写字母。例如输入 q[回车] 时,会输出 Q。
输入格式
无
输出格式
无
输入
输入 #1
q输出样例
输出 #1
Q
题目分析:
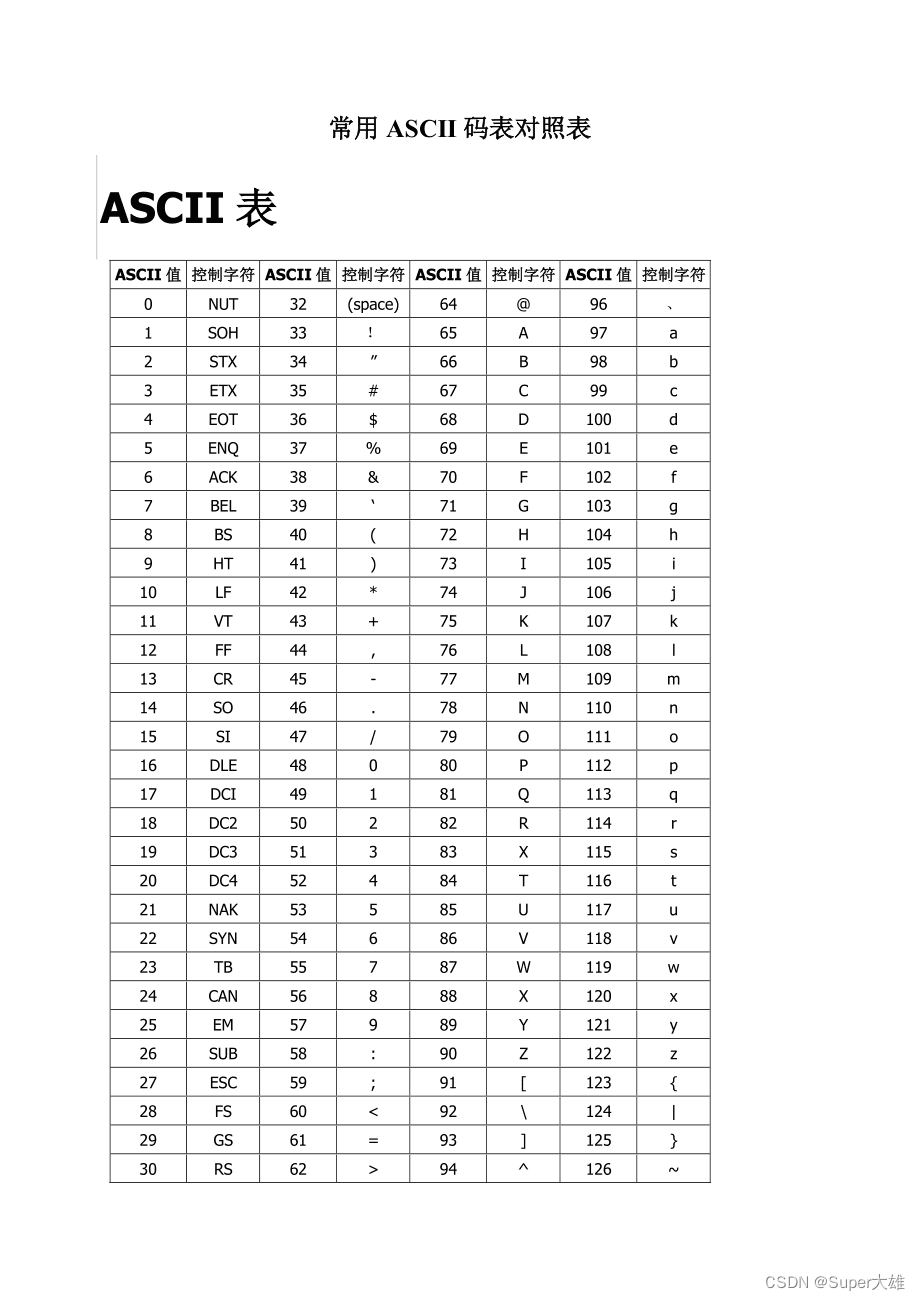
- 本题目主要考察的是大小写字母的ASCII码,大写字母A的ascii码为65,而小写字母a的acsii码为97,由此我们可以确定大小写字母之间的ascii码之间相差32。
- 可以使用String类的toUpperCase()方法将小写字母转换为大写字母。
知识点:
toUpperCase()方法
代码如下
static void fun(){Scanner sc=new Scanner(System.in);String str=sc.next();System.out.println(str.toUpperCase());}🍋3. 再分肥宅水
题目描述
现在有 t 毫升肥宅快乐水,要均分给 n 名同学。每名同学需要 2 个杯子。现在想知道每名同学可以获得多少毫升饮料(严格精确到小数点后 3 位),以及一共需要多少个杯子。
输入格式
输入一个实数 t 和一个正整数 n,使用空格隔开。
输出格式
输出两行。
第一行输出一个三位小数,表示可以获得多少毫升饮料。第二行输出一个正整数,表示一共需要多少个杯子。
输入输出样例
输入 #1
500.0 3输出 #1
166.667 6说明/提示
对于所有数据,0≤t≤100000≤t≤10000 且小数点后不超过 3 位,1≤t≤10001≤n≤1000。
题目分析:
- 先把快乐肥宅水分给n个学生,及使用总量除以学生的个数。
- 每个学生两个杯子,则n个学生n*2个杯子。
知识点:
常用保留小数点位数的方法:
1.使用String.format()字符串格式输出
format("输出格式",数值),"%.保留的小数位数f",按照四舍五入进行保留小数位数。
2.使用数学函数Math.round() 四舍五入
double d = 12.344345; //保留两位小数long num = Math.round(d * 100);System.out.println(num / 100.0);3.使用BigDecimal类,可以进行复杂的保留小数位数,进行高精度运算时常使用。
BigDecimal bd=new BigDecimal( 12.344345);System.out.println(bd.setScale(2,BigDecimal.ROUND_DOWN));使用BigDecimal类中的setScale()函数设置需要保留的小数位数和保留小数位数的格式。我们上边是使用BigDecimal中的静态量,ROUND_DOWN.可以替换为以下的内容。
常用:
个人认为:四舍五入
ROUND_UP:舍入模式从零开始。 始终在非零丢弃分数之前增加数字。
个人认为:直接截断
ROUND_DOWN:舍入模式向零舍入。 不要在丢弃的分数之前递增数字(即截断)。4.DecimalFormat类
// 构造方法设置格式 DecimalFormat df=new DecimalFormat("#.00");String str=df.format(12.345345);System.out.println(str);#.00:#表示一个数字,0显示为缺省(即空字符),.就表示他本来的意思,0表示一个数字,00表示两个数字。
代码如下
Scanner sc=new Scanner(System.in);double t=sc.nextDouble();int n=sc.nextInt();
// String.format ("%.1f", num)System.out.println(String.format("%.3f",t/n));System.out.println(2*n);🥭4. 数字反转
题目描述
输入一个不小于 100 且小于 1000,同时包括小数点后一位的一个浮点数,例如 123.4 ,要求把这个数字翻转过来,变成 4.321 并输出。
输入格式
一行一个浮点数
输出格式
一行一个浮点数
输入输出样例
输入 #1
123.4输出 #1
4.321
题目分析:
- 对数值进行翻转,把数值转换为字符串使用StringBuild类中的reverse()函数进行对字符串进行翻转
知识点:
1.String类中的方法修改时不会修改本身,除非再次对String类进行赋值,而StringBuilder和StringBuffer类对类使用方法时会自动修改原来的类。
代码如下
Scanner sc = new Scanner(System.in);double n= sc.nextDouble();String str=String.valueOf(n);System.out.println(new StringBuilder(str).reverse());总结
通过几道简单的例题,通过对以下内容的复习:
- for循环的复习和控制空格字符的输出。
- 可以了解ascii码之间的转换规律。
- 牢牢记住保留指定位数的小数。
- reverse()实现对字符串的倒置。
