怎样做电影下载网站中小企业网站模板
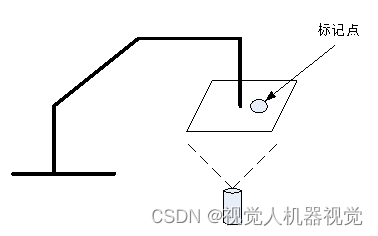
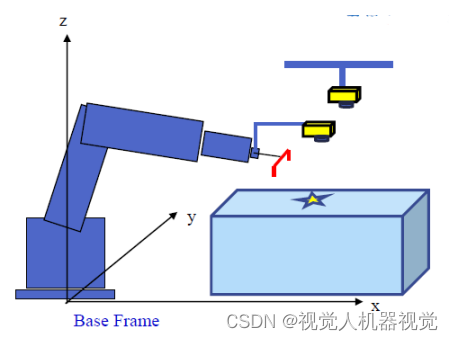
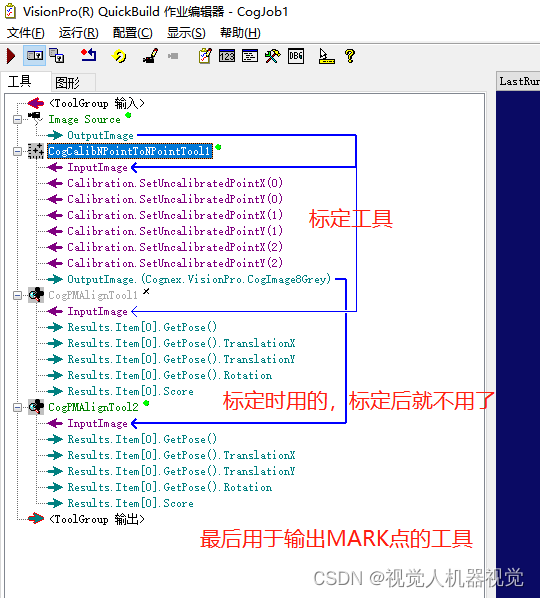
1、机器人吸取电路板,移动到拍照位置,并在电路板上找一个标记点,并且,通过机器人示教把当前电路板能够准确的放入到目标位置。
2、机器人吸取电路板吸取电路板,在x,y方向进行移动,总共移动4个位置,记录4个位置的机器人的坐标,以及拍摄图像
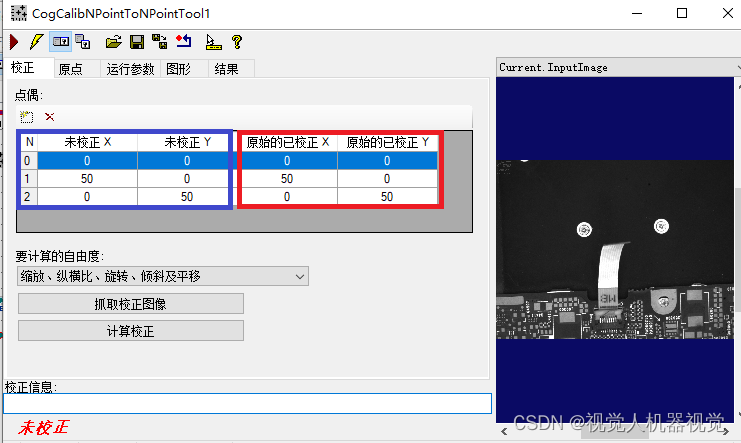
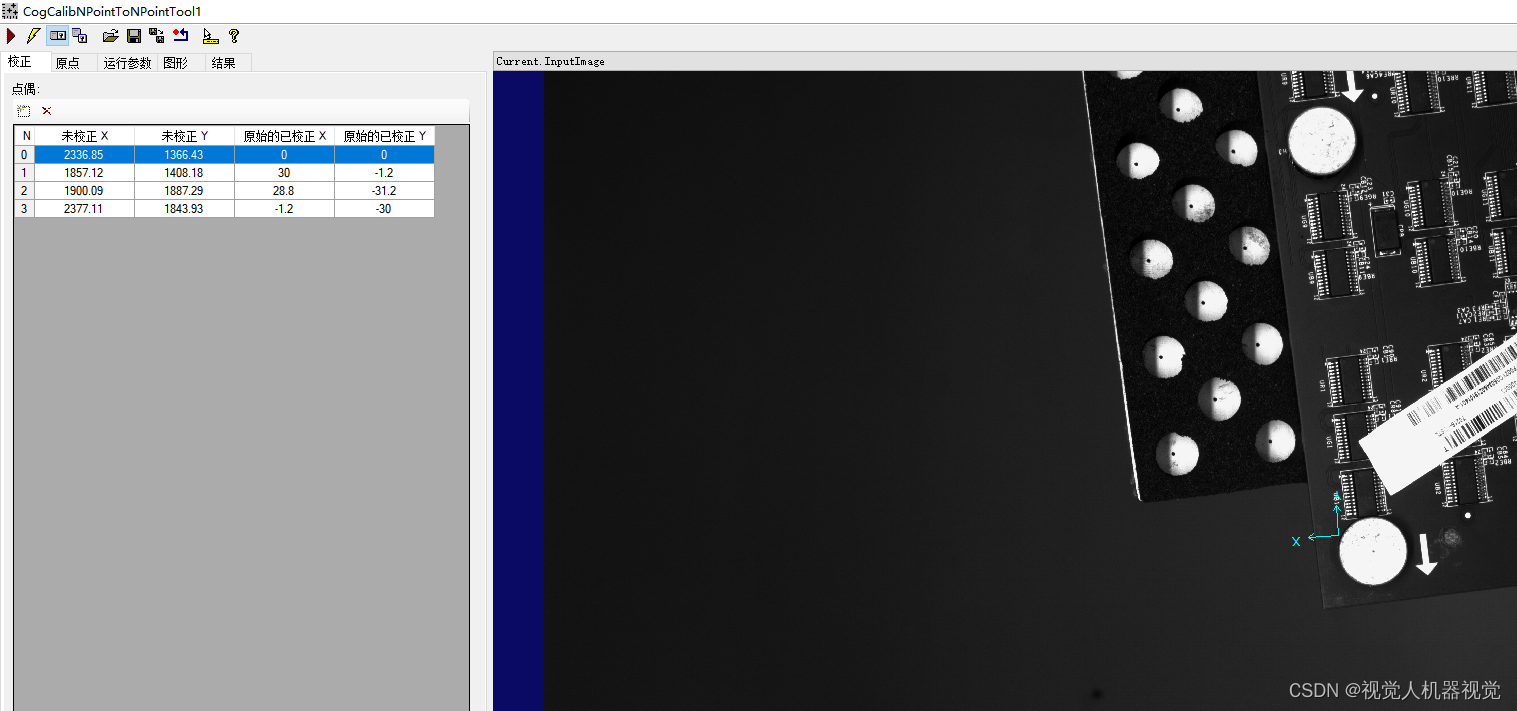
3、使用vp的CogCalibNpointToNpoint工具,并在蓝框填入标志点的像素坐标,红框填入对应的机器人坐标。
4.点运行完成标定功能。
5、完成标定后,整个流程如下
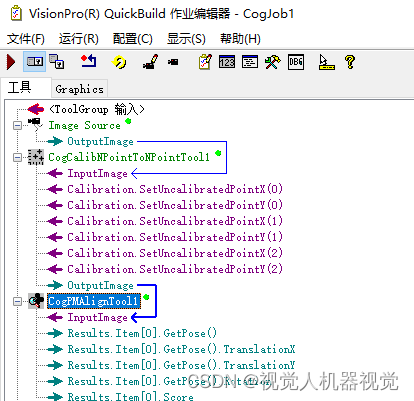
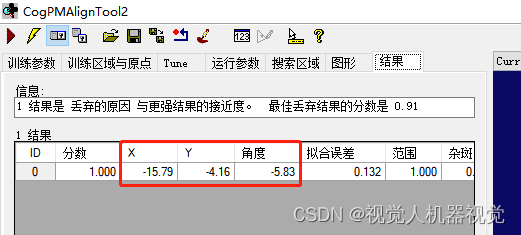
在模板匹配中把模板中心进行记录。然后,调整标定工具的校正原点
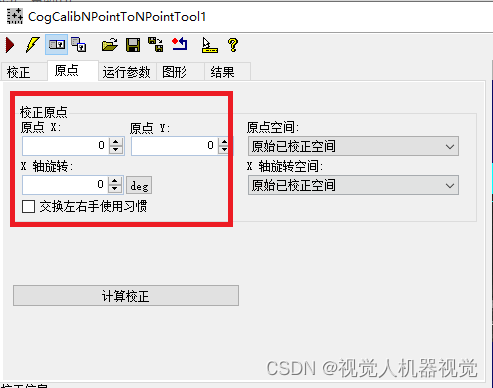
使得模板匹配的模板中心x,y坐标输出为0,0,表示当前吸取的电路板能够准确的放入模板位置
下次,再吸取电路板时,执行模板匹配后,输出的x,y坐标就是机器人应当移动的x,y的偏移量
这样x y 就计算完成了。
但往往,因为还有旋转。所以还要计算角度
机器人不用旋转中心进行标定
旋转中心标定方式的说明
在下面的图例中,红色为相机视野(FOV),黄色为工件,五星为Mark点。



旋转中心方法用于所有机器人与视觉配合场景
方法 :计算工件实际发生的偏移量 和旋转,结合机器人的旋转中心进行二次补偿后 ,把补偿量 发送给机器人 ,然后机器人把补偿量进行抓取或放置即可。
计算 某个点绕另外一旋转定角度后的坐 标,如图 :A(x,y)绕 B(rx0 ,ry0) 旋转a度后的位置为 C(x0,y0 ),则有如 下关系式:
x0= cos (a) * (x -rx0) – sin (a) *(y-ry0) +rx0
y0= cos (a) * (y- ry0) + sin (a) (x-rx0) +ry0
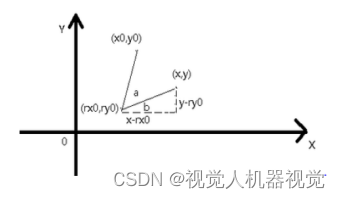
下面的所有计算旋转与偏移量都是基于上面的公式。
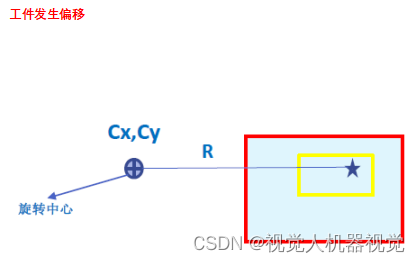
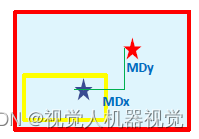
{Cx,Cy } 旋转中心坐标; {Mx,My } 工件 Mark坐标。
{MDx,MDy},Mark偏移量。
{RDx,Rdy}, 发送给机器人的补偿量。
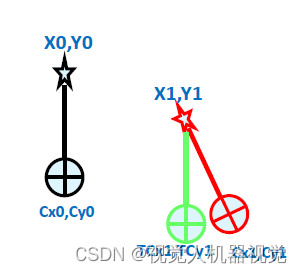
工件发生平移时,
在拍照位置进行拍照后 ,与开始训练标准位置时,Mark点成像会产生偏移。
Mark 偏移量 MDx =RDx;MDy =RDy ;
如上图即相机计算出的 Mark 点偏移量 ,可以直接补偿给机器人,然后进行抓取即可。
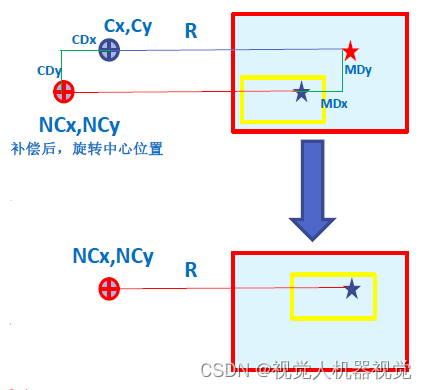
作为测试 ,可以机器人在拍照位置进行补偿后 ,Z轴不变然后再拍照 ,会获得和拍照位置一样的图像。
工件发生平移与旋转
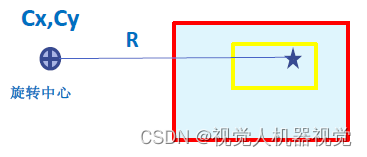
工件发生平移和旋转时
在拍照位置进行后 ,与开始训练标准位置时 ,Mark 点成像会产生偏移;
Mark 偏移量 MDx #RDx, MDy#RDy ;如左上图即相机计算出的 MarkMark 点偏移量 ,不能直接补偿给机器人 ,需要计算出 RDx 和RDy,和RDr ,MDr 然后补偿给机器人 ,机器人补偿后才能进行抓取。
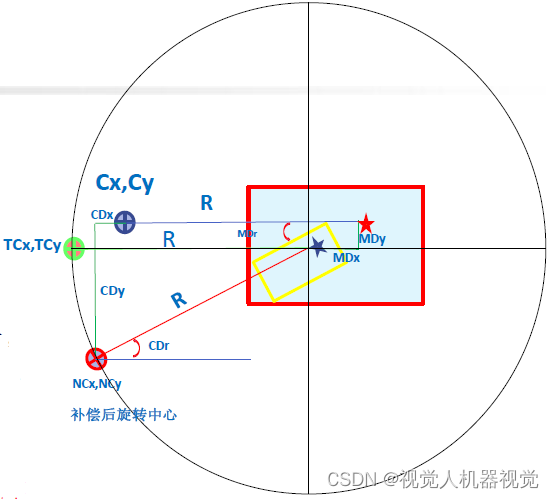
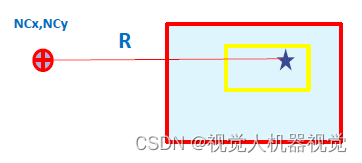
作为测试 ,可以机器人在拍照位置进行补偿后 ,Z轴不变然后再拍照 ,会获得和拍照位置一样的图像;
计算过程,旋转角度a
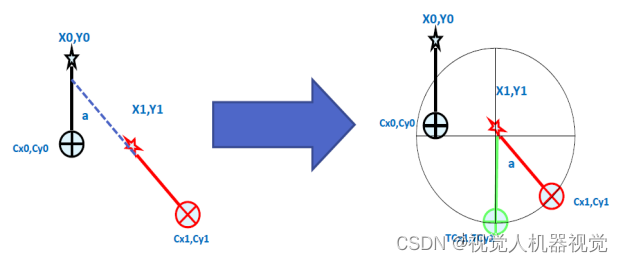
计算 CDx =Cx1– Cx0和 CDy =Cy1– Cy0
CDx = cos (a) * (Cx0 -X0) -sin (a) * Cy0-Y0) + X1 – Cx0
CDy = cos (a) * (Cy0 -Y0 ) + sin (a) * Cx0 -X0 ) + Y1– Cy0
从公式中可以看出,补给机器人的偿量由:
旋转中心坐标( Cx0,Cy0 )
标准的工件 (Mark) 坐标点( X0,Y0)
工件移动后新的(Mark)坐标点
工件 (Mark) 旋转角度 a
所以利用旋转中心方法计算给机器人的补偿量时,首先要中心坐标,
但是在很多场景下计算旋转中心坐标时要么出了视野,要么转的角度范围太小等,拟合旋中心都存在误差,
导致补偿精不够
一定要计算旋转中心坐标吗?其实不需要。
CDx,Cdy 计算过程 ,旋转角度 a
CDx = cos (a) * (Cx0 -X0) -sin (a) * (Cy0 -Y0) + X1 – Cx0
= ( cos (a) -1) * (Cx0-X0)-Sin(a)(Cy0 -Y0) + MDx
= (cos(a) -1) * StDx -sin (a) * StDy + MDx
CDy = cos ( a) * (Cy0 -Y0 ) + sin (a) * (Cx0 -X0 ) +y1 – Cy0
= ( cos (a) -1) * (Cy0 -Y0 ) + sin (a) * (Cx0 -X0 ) + Mdy
= (cos(a) -1) * StDy + sin (a) * StDx + Mdy
从公式中可以看出 StDx= Cx0-X0, StDy = Cy0 -Y0 是个常量, MDx 和Mdy是每次拍照是工件 (Mark )的坐标与准位置工件( Mark)的差值;
StDx 与StDy 怎么计算呢?蓝色的为一个二元次方程,我们需要旋转角度即可计算出;
如果 计算出 StDx 和StDy 则在运行时,直接带入上述公式,可以很快计算出 CDx,Cdy 这样给出Robot 的偏移量了,而不需要计算旋转中心确切坐标了
下面介绍如何求解 StDx和StDy
实际操作的时候,感觉上面的文章有点难理解,就还是老老实实去算了圆心,例如让机器人旋转正15度,和负15度,得到两个新的坐标。3点求圆心坐标。
点求圆心:
struct POINT
{ public double X;public double Y; } POINT RotateCenterCal(POINT p1, POINT p2, POINT p3, POINT ptCenter){//将三点代入圆的方程double a = 2 * (p2.X - p1.X);double b = 2 * (p2.Y - p1.Y);double c = p2.X * p2.X + p2.Y * p2.Y - p1.X * p1.X - p1.Y * p1.Y;double d = 2 * (p3.X - p2.X);double e = 2 * (p3.Y - p2.Y);double f = p3.X * p3.X + p3.Y * p3.Y - p2.X * p2.X - p2.Y * p2.Y;ptCenter.X = (b * f - e * c) / (b * d - e * a);ptCenter.Y = (d * c - a * f) / (b * d - e * a);return ptCenter;}
之后可以根据圆心 以及当前取得到的坐标以及旋转量,倒推得到要旋转多少角度和移动多少坐标才能回正。
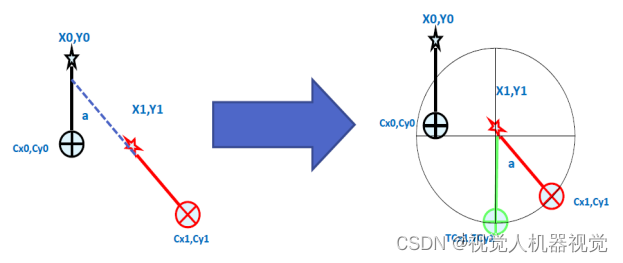
CDx = cos (a) * (Cx0 -X0) -sin (a) * Cy0-Y0) + X1 – Cx0
CDy = cos (a) * (Cy0 -Y0 ) + sin (a) * Cx0 -X0 ) + Y1– Cy0
从公式中可以看出,补给机器人的偿量由:
旋转中心坐标( Cx0,Cy0 )
标准的工件 (Mark) 坐标点( X0,Y0)
工件移动后新的(Mark)坐标点
工件 (Mark) 旋转角度 a
代码: private void button3_Click(object sender, EventArgs e)
{ //根据圆心坐标 与角度, 以及原先的X,Y, 求旋转角度后的新坐标
POINT p1 = new POINT();
POINT p2 = new POINT();
POINT presult = new POINT();
p1.X = double.Parse(lastX.Text);p1.Y = double.Parse(lastY.Text);double jiaodu = double.Parse(lastjiaodu.Text);jiaodu = -jiaodu;// jiaodu = jiaodu * 180 / Math.PI; 无需转换成度数p2.X = double.Parse(centerX.Text);p2.Y = double.Parse(centerY.Text);presult = FindNEWXandY(p1, p2, presult, jiaodu);resultX.Text = presult.X.ToString();resultY.Text = presult.Y.ToString();}POINT FindNEWXandY(POINT p1, POINT p2,POINT presult,double jiaodu){//根据圆心坐标 与 原先的X,Y, 求旋转角度后的新坐标//jiaodu = (Math.PI *jiaodu/180);double mc = Math.Cos(jiaodu);double ma = Math.Sin(jiaodu);double a1 = (p1.X - p2.X) * mc;double b1 = (p1.Y - p2.Y) * ma;presult.X =Math.Round(a1 - b1 + p2.X,3);double a2= (p1.Y - p2.Y) * mc;double b2 = (p1.X - p2.X) * ma;presult.Y = Math.Round(a2 + b2 + p2.Y,3);return presult;}
因为当时使用的机器人精度较查,误差还是挺大的。如果项目成型,则会有最终解决方案,目前只是配合测试。先到此结束
