网站免费建站方法做网站图片格式
1、什么是Stream流
Lambda表达式,基于Lambda所带来的函数式编程,又引入了一个全新的Stream概念,用于解决集合类库既有的鼻端。
2、案例
假设现在有一个需求, 将list集合中姓张的元素过滤到一个新的集合中;然后将过滤出来的姓张的元素中,再过滤出来长度为3的元素,存储到一个新的集合中
// 已知的知识来解决需求
List<String> list1 = new ArrayList<>();
list1.add("张老三");
list1.add("张小三");
list1.add("李四");
list1.add("赵五");
list1.add("张六");
list1.add("王八");ArrayList<String> list2 = new ArrayList<>();
// 1.将list集合中姓张的元素过滤到一个新的集合中
for(String name : list1){if(name.startsWith("张")){list2.add(name);}
}
ArrayList list3 = new ArrayList();
for (String name : list2) {if (name.length() == 3){list3.add(name);}
}
System.out.println(list3);很麻烦,不是吗,同样我们需要更加简洁优雅的方式实现 (链式调用)
3、 Stream流
list1.stream().filter((String name)->name.startsWith("张")).filter((String name)->name.length()==3).forEach((String name)->{System.out.println("符合条件的姓名:" + name);
});4、获取流的方式
Stream<String> stream1 = list.stream();
Stream<String> stream2 = set.stream();//根据Map集合的键获取流
Set<Integer> map1 = map.keySet();
Stream<Integer> stream3 = map1.stream();
//根据Map集合的值获取流
Collection<String> map2 = map.values();
Stream<String> stream4 = map2.stream();
//根据Map集合的键值对对象获取瑞
Set<Map.Entry<Integer, String>> map3 = map.entrySet();
Stream<Map.Entry<Integer, String>> stream5 = map3.stream();
// 根据数组获取流
String[] arr = {"张颜宇","张三","李四","赵五","刘六","王七"};
Stream<String> stream6 = Stream.of(arr);5、Stream流的常用方法
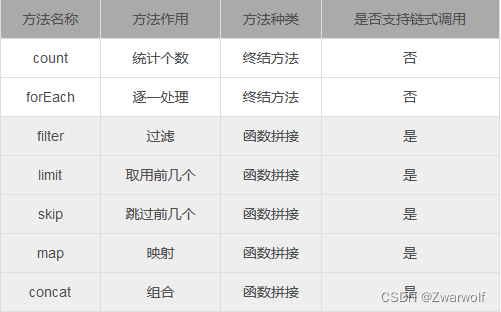
1)、count方法
List<String> list = new ArrayList<>();list.add("张老三");list.add("张小三");list.add("李四");list.add("赵五");list.add("张六");list.add("王八");long count = list.stream().count();System.out.println("集合中的元素个数是:" + count);//输出结果://集合中的元素个数是:62)、filter 方法
// 获取stream流
Stream<String> stream = Stream.of("张老三", "张小三", "李四", "赵五", "刘六", "王七");
// 需求:过去出姓张的元素
stream.filter((String name)->{return name.startsWith("张");
}).forEach((String name)->{System.out.println("流中的元素" + name);
});3)、foreach 方法
List<String> list = new ArrayList<>();
list.add("张老三");
list.add("张小三");
list.add("李四");
list.add("赵五");
list.add("张六");
list.add("王八");// 函数模型:获取流 --> 注意消费流中的元素
list.stream().forEach((String name)->{System.out.println(name);
});4)、limit方法
// 获取流的长度
Stream<String> stream1 = Stream.of("张老三", "张小三", "李四", "赵五", "刘六", "王七");
// 需求:保留前三个元素
stream1.limit(3).forEach((String name)->{System.out.println("流中的前三个元素是:" + name);
});5)、map方法
//基本类型转换
// 获取Stream流
Stream<String> stream1 = Stream.of("11","22","33","44","55");
// 需求:把stream1流中的元素转换为int类型
stream1.map((String s)->{return Integer.parseInt(s); // 将String类型的s进行转换为Integer类型的元素,并返回
}).forEach((Integer i)->{System.out.println(i); // 将转换后的int类型的元素逐一输出
});//大写转换收集
List list = new ArrayList<>();
list.add("apple");
list.add("banana");
list.add("orange");
Stream stream = list.stream().map(s -> s.toUpperCase());
stream.forEach(System.out::println);//元素计算收集
List list = Arrays.asList(1, 2, 3, 4, 5);
List resultList = list.stream().map(x -> x * x).collect(Collectors.toList());
System.out.println(resultList);//引用数据类型属性收集
List people = new ArrayList<>();
people.add(new Person("Tom", 18));
people.add(new Person("Jerry", 20));
List result = people.stream().map(Person::getName).collect(Collectors.toList());
System.out.println(result);//实体类map类型收集
List people = new ArrayList<>();
people.add(new Person("Tom", 18));
people.add(new Person("Jerry", 20));
Map result = people.stream().collect(Collectors.toMap(Person::getName, Person::getAge));
System.out.println(result);6)、skip方法
// 获取stream流
Stream<String> stream = Stream.of("张老三", "张小三", "李四", "赵五", "刘六", "王七");
stream.skip(3).forEach((String name)->{System.out.println("跳过前三个,打印剩下的" + name);
});7)、concat方法
Stream<String> stream1 = Stream.of("11","22","33","44","55");
Stream<String> stream2 = Stream.of("张颜宇", "张三", "李四", "赵五", "刘六", "王七");
// 需求:合并两个流
Stream<String> stream = Stream.concat(stream1,stream2);
stream.forEach((String name)->{System.out.print(name);
});8)、收集Stream流方法
List<String> list2 = new ArrayList<>();
list2.add("张老三");
list2.add("张小三");
list2.add("李四");
list2.add("赵五");
list2.add("张六");
list2.add("王八");// 需求:过滤出姓张的并且长度为3的元素
Stream<String> stream = list2.stream().filter((String name) -> {return name.startsWith("张");
}).filter((String name) -> {return name.length() == 3;
});// stream 收集到单列集合中
List<String> list = stream.collect(Collectors.toList());
System.out.println(list);// stream 收集到单列集合中
Set<String> set = stream.collect(Collectors.toSet());
System.out.println(set);public class StreamTest {public static void main(String[] args) {List<String> names = new ArrayList<>();//Collections.addAll();Collections.addAll(names,"张三丰","张无忌","李四","王五","李娜","吴彦祖");
// System.out.println(names);// for (String s:names) {
// //打印所有姓张的
// if(s.startsWith("张")){
// System.out.println(s);
// }
// //打印出所有名字长度是3的
// if(s.length()==3){
// System.out.println(s);
// }
// }//Stream 流实现集合过滤//1. 通过集合获取流Stream<String> s1 = names.stream();//2. 过滤器 filter 遍历器 foreach//过滤出所有姓张的姓名
// s1.filter((String name) -> name.startsWith("张"))
// .forEach((String name) -> {
// System.out.println(name);
// });//limit(X) 取前X个数据Stream<String> stm2 = Stream.of("张小毛","赵本山","吴亦凡","曹孟德","刘备","李斯");
// stm2.limit(3).forEach((String s) -> System.out.println(s));//skip(X) 跳过X个数据,打印剩下的
// stm2.skip(3).forEach((String s) -> System.out.println(s));//concat(流1,流2) 合并流1和流2 (泛型最好相同)Stream<String> stream3 = Stream.of("11","22","33","44","55");//合并两个流存到stmAll中
// Stream<String>stmAll = Stream.concat(stm2,stream3);
// stmAll.forEach((String s) -> System.out.println(s));//map 映射
// stream3.map((String n) -> {
// return Integer.parseInt(n);
// }).forEach((Integer num)-> System.out.println(num));// stream3.map((String number) -> {
// number = "100";
// return number;
// }).forEach((String n) -> System.out.println(n));Stream<String> stm4 = Stream.of("张小毛","赵本山","吴亦凡","曹孟德","刘备","李斯");//挑选出3个字名字,并且存入一个List中List ss = stm4.filter((String name) ->name.length() == 3).collect(Collectors.toList()); //collect收集方法:将过滤出来的数据转为集合//Collectors.toList()转为什么集合toList List集合//关闭stm4.close();System.out.println(ss);// AtomicInteger sum = new AtomicInteger();
// AtomicInteger sum_mew = new AtomicInteger();
// stream3.map((String n) -> {
// sum.set(Integer.parseInt(n) + sum.get());
// return sum;
// }).forEach((AtomicInteger num)-> {
// sum_mew.set(num.get());
// });
// System.out.println("总和为:"+sum_mew);}
}9)、Stream流的reduce方法
//利用reduce方法快捷运算
List numbers = Arrays.asList(1, 2, 3, 4, 5);
int sum = numbers.stream().reduce((a, b) -> a + b).get();
System.out.println(sum);本电子书目录:《Java基础的重点知识点全集》
