顺企网宁波网站建设免费做微信请帖的网站
介绍
使多个 Redis 实例共同工作,实现数据的水平扩展。通过将数据分片到多个节点上,Redis 集群能够在不牺牲性能的前提下扩展存储容量和处理能力,从而支持更高并发的请求。Redis 集群不仅支持数据分片,还提供了自动故障转移和高可用性功能。

这些主节点会相互的ping来达到自动故障转移
特点
- 集群中有多个master,每个master保存不同数据
- 每个master都可以有多个slave节点
- master之间通过ping监测彼此健康状态 就不用哨兵了
部署文件
version: "3.2"services:r1:image: rediscontainer_name: r1network_mode: "host"entrypoint: ["redis-server", "--port", "7001", "--cluster-enabled", "yes", "--cluster-config-file", "node.conf", "--requirepass", "mypassword","--masterauth", "yourpassword"]r2:image: rediscontainer_name: r2network_mode: "host"entrypoint: ["redis-server", "--port", "7002", "--cluster-enabled", "yes", "--cluster-config-file", "node.conf", "--requirepass", "mypassword","--masterauth", "yourpassword"]r3:image: rediscontainer_name: r3network_mode: "host"entrypoint: ["redis-server", "--port", "7003", "--cluster-enabled", "yes", "--cluster-config-file", "node.conf", "--requirepass", "mypassword","--masterauth", "yourpassword"]r4:image: rediscontainer_name: r4network_mode: "host"entrypoint: ["redis-server", "--port", "7004", "--cluster-enabled", "yes", "--cluster-config-file", "node.conf", "--requirepass", "mypassword","--masterauth", "yourpassword"]r5:image: rediscontainer_name: r5network_mode: "host"entrypoint: ["redis-server", "--port", "7005", "--cluster-enabled", "yes", "--cluster-config-file", "node.conf", "--requirepass", "mypassword","--masterauth", "yourpassword"]r6:image: rediscontainer_name: r6network_mode: "host"entrypoint: ["redis-server", "--port", "7006", "--cluster-enabled", "yes", "--cluster-config-file", "node.conf", "--requirepass", "mypassword","--masterauth", "yourpassword"]部署
docker-compose up -d
集群连接
进入任意节点容器
docker exec -it r1 bash
连接
将各个节点进行连接
- redis-cli --cluster:代表集群操作命令
- create:代表是创建集群
- –cluster-replicas 1 :指定集群中每个master的副本个数为1
- 此时节点总数 ÷ (replicas + 1) 得到的就是master的数量n。因此节点列表中的前n个节点就是master,其它节点都是slave节点,随机分配到不同master
redis-cli --cluster create --cluster-replicas 1 \
13.116.247.215:7001 13.116.247.215:7002 13.116.247.215:7003 \
13.116.247.215:7004 13.116.247.215:7005 13.116.247.215:7006 \
-a mypassword

查看集群状态
redis-cli -p 7001 -a mypassword cluster nodes
散片插槽
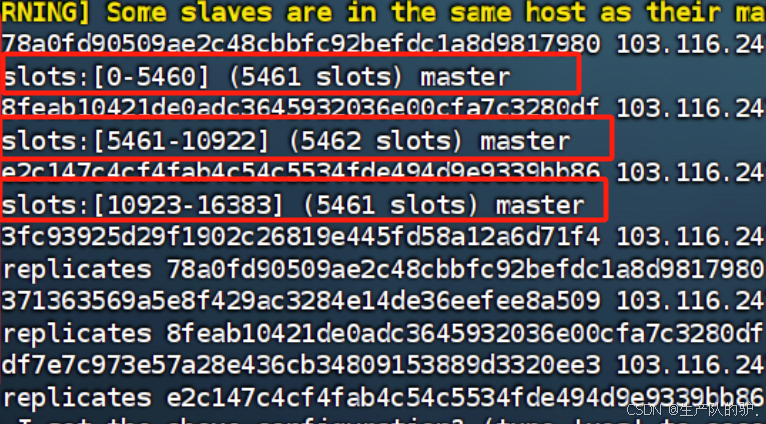
创建成功后 每一个主节点都会分配哈希散片插槽,Redis数据不是与节点绑定,而是与插槽slot绑定。当我们读写数据时,Redis基于CRC16算法对key做hash运算,得到的结果与16384取余,就计算出了这个key的slot值。然后到slot所在的Redis节点执行读写操作。
](https://i-blog.csdnimg.cn/direct/d1845492a296446d914f59cf3e3b1672.png)
