网站建设基础知识六安市城市建设档案馆网站
印象笔记04: 如何将印象笔记超级会员价值最大化利用?
为什么有这个问题
我不知道有没有人一开始接触印象笔记觉得非常好。奈何只能两个设备同步,局限太多。而会员活动比较优惠——就开了会员。而且我开了十年……。只能开发一下看看怎么最大化利用会员价值了。
自己搜了一圈,发现没有人干这个事情,那我做吧,我思考一下如何最大化利用。
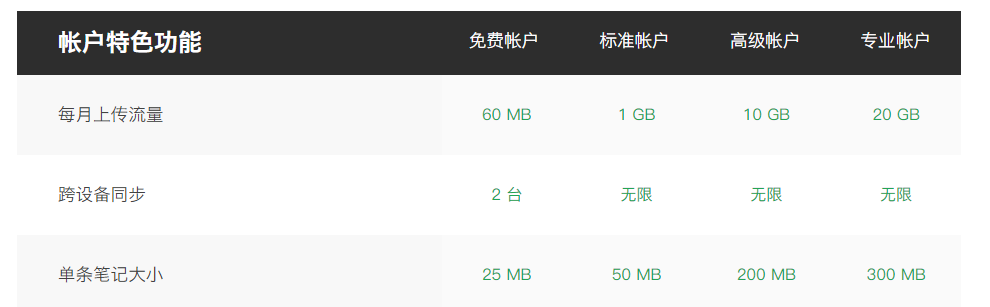
先看有哪些功能

https://static.app.yinxiang.com/pay/subscriptions?itemCode=pro-1year&redirect=true
实在是太多了 详见网址。
主要是:
- AI礼包

- 流量20g每月、笔记容量大等
- 模版随便用
- 1000张OCR
- 字体随便用
在另一个链接里 ,有不同类型的详细比对:
类型比对
如何最大化利用——印象笔记会员功能使用究极清单
1. 所有的设备都装上印象笔记并同步
免费账户只能用2个设备,会员功能均不限制设备。这意味着可以在所有设备上安装印象笔记并同步。(注意:Linux不行&……)。本人一部手机,两个平板,四台笔记本电脑和两个台式机,全部都装上。
2. 可以保存一些重要图片和重要文件
专业账户每个月有20G流量上传下载额度。相比于免费版的60M简直天壤地别。我开通专业版账户后也搜过,实在是没什么消耗流量的好办法。尝试过上传视频文件、上传书籍PDF(大于100m的)。可能是高估服务器了,上传时候总会卡死……
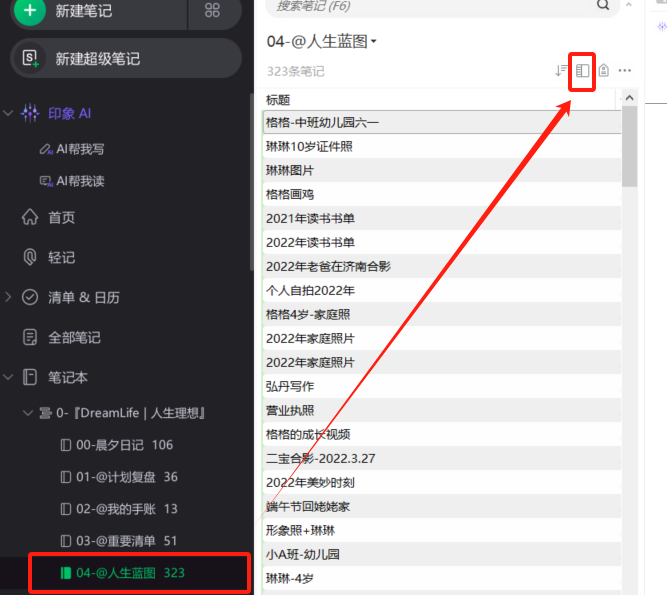
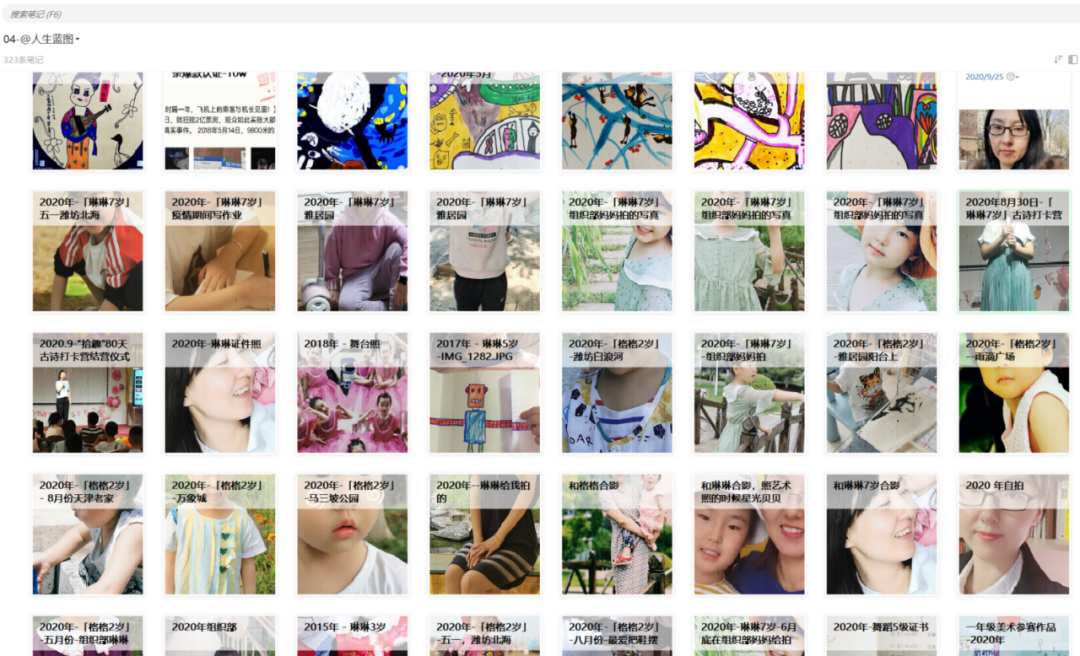
这里看到有一个博主推文在印象笔记里备份照片,那可太合适了!
图片来源: https://mp.weixin.qq.com/s/zJX4SSxFac-M3d6ew3q1BA
选择”卡片视图“,这样就能非常清楚的看到图片里面的内容,有很强烈的视觉体验,也便于我们查找某张特定图片。
另外可以尝试当坚果云使用:使用同步功能。

此外,我也尝试将学校单位的一些文件、规章制度和自己整理的文件材料放在印象笔记里,可以随时查看。一个pdf几个M。当然每月用不了20G,至少消耗到大于标准用户的1G就很满意了,
3. 总得有条笔记299M。
在笔记里放附件和视频吧这是……我知道音频导入印象笔记可以根据时间点记录笔记。
4.每月OCR扫描
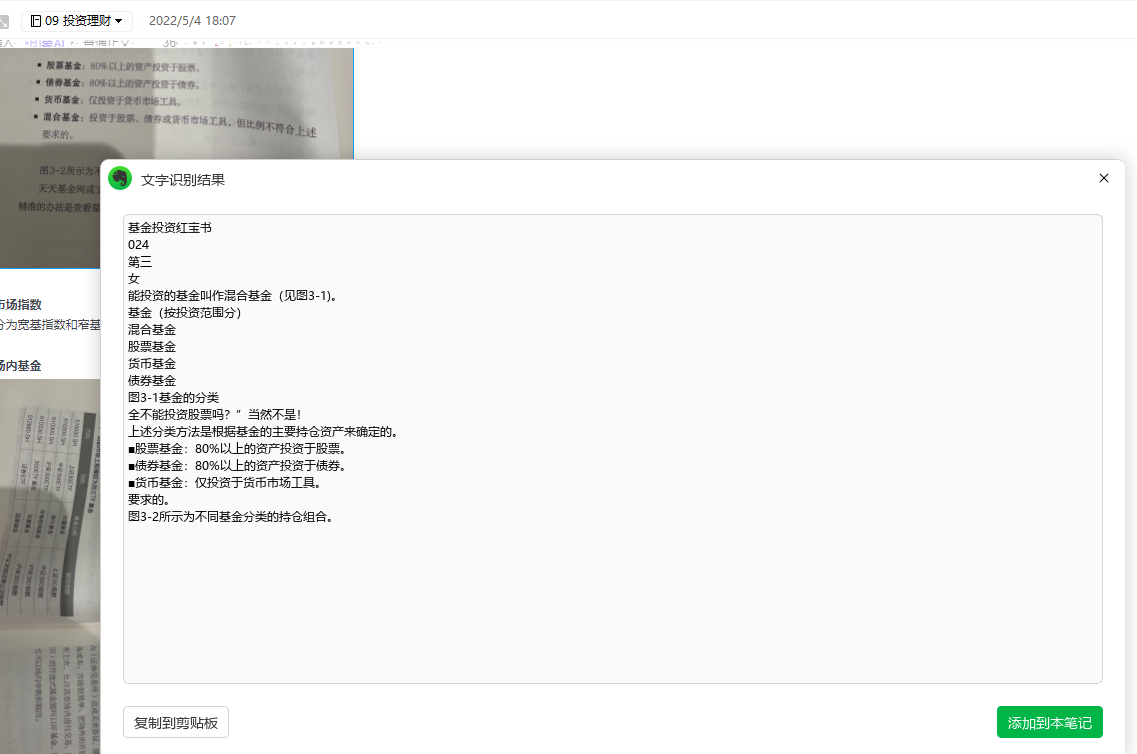
专业版每个月有1000张OCR扫描额度,完全够用。完全用不完。根据测试,OCR识别主要应用在APP端,直接拍照OCR识别。

在使用印象笔记进行拍照扫描时,只需开启 OCR 模式,并对准需要扫描识别的文件,就能快速扫描识别并提取图片中的文字,并能一键复制或存入笔记中。
应用场景推荐:
在书店读书的时候能够用到:实体书好的地方直接拍照扫描,非常方便。
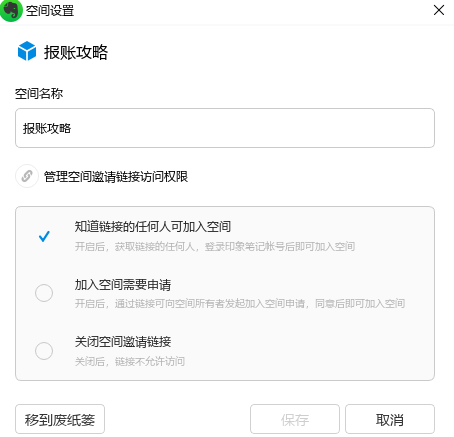
- 创建和使用空间
参考教程:https://www.comcw.cn/jc/9910.html
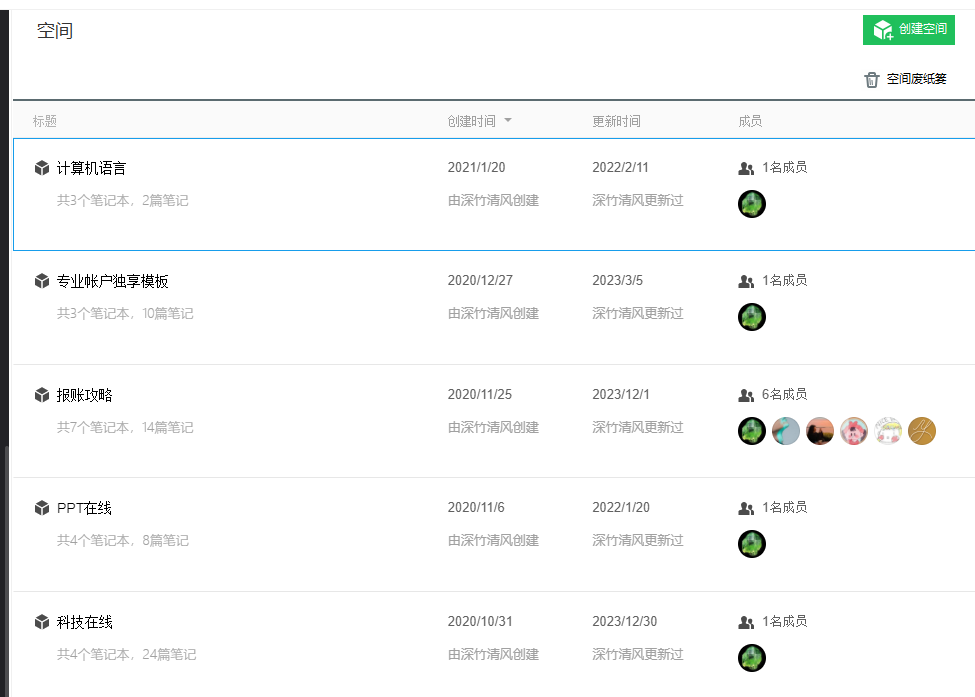
专业账户和超级会员都能够创建和分享500个空间,每个空间可以容纳500人。
这意味着可以做类似于语雀等的知识分享功能。
- 录屏
MAC端可以录屏。
https://staging.yinxiang.com/hc/articles/mac%E5%AE%A2%E6%88%B7%E7%AB%AF%E5%BD%95%E5%B1%8F%E5%8A%9F%E8%83%BD%E4%BD%BF%E7%94%A8%E8%AF%B4%E6%98%8E/
- 印象AI会员
只有超级会员具有这个权限。可以使用AI来做一些工作。
比如:在印象笔记写笔记的时候,用一下AI直接辅助查询和撰写一些文字。
不限次数,那就努力调用吧,也不是很好用。

但是知识星图、双向链接、自动生成标签还是方便一点。
8.同时获得 5 大效率工具会员
轻记、剪藏、印象时间、印象图记和Verse都可以用。在电脑上除了Verse都是一起的。但是手机分别是不同的应用。个人比较喜欢印象时间,在地铁上记录一下,电脑也能同步。
