电影网站设计说明书二级域名网站免费申请
Unity SVN更新提交小工具
- 前言
- 使用说明
- 必要前提
- 源码
- 参数说明
- 感谢
前言
Unity开发时每次都要到文件夹中操作SVN,做了一个小工具能够在Editor中直接操作。
使用说明
必要前提
前提是要安装好SVN,在文件夹右键能够看到安装的SVN
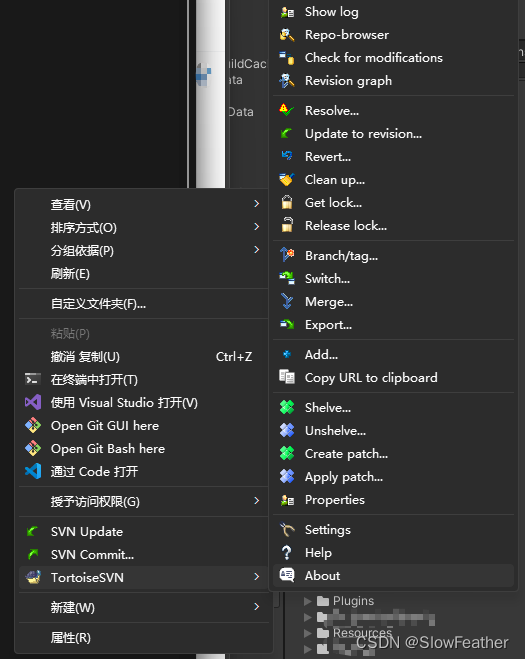
源码
using System.Collections.Generic;
using UnityEditor;
using UnityEngine;/// <summary>
/// 每次打开文件夹操作太麻烦,所以GUI比较方便
/// </summary>
public class SVNHelper : EditorWindow
{[MenuItem("SVN Helper/自信更新 CertainUpdate", false, 1)]static void SVNCertainUpdate(){ProcessCommand("TortoiseProc.exe", " /command:update /path:" + SVNProjectPath + " /closeonend:3");}/// <summary>/// 提交当前项目的SVN/// </summary>[MenuItem("SVN Helper/提交 Commit")]static void SVNCommit(){List<string> pathList = new List<string>();string basePath = SVNProjectPath + "/Assets";pathList.Add(basePath);//pathList.Add(SVNProjectPath + "/ProjectSettings");string commitPath = string.Join("*", pathList.ToArray());ProcessCommand("TortoiseProc.exe", "/command:commit /path:" + commitPath);}[MenuItem("SVN Helper/更新 Update")]static void SVNUpdate(){ProcessCommand("TortoiseProc.exe", "/command:update /path:" + SVNProjectPath + " /closeonend:0");}[MenuItem("SVN Helper/清理 CleanUp")]static void SVNCleanUp(){ProcessCommand("TortoiseProc.exe", "/command:cleanup /path:" + SVNProjectPath);}[MenuItem("SVN Helper/记录 Log")]static void SVNLog(){ProcessCommand("TortoiseProc.exe", "/command:log /path:" + SVNProjectPath);}/// <summary>/// 当前项目路径/// </summary>static string SVNProjectPath{get{System.IO.DirectoryInfo parent = System.IO.Directory.GetParent(Application.dataPath);return parent.ToString();}}public static void ProcessCommand(string command, string argument){// 创建进程启动信息对象System.Diagnostics.ProcessStartInfo info = new System.Diagnostics.ProcessStartInfo(command);// 设置进程启动参数info.Arguments = argument;info.CreateNoWindow = false;info.ErrorDialog = true;info.UseShellExecute = true;// 如果使用shell执行,则不重定向标准输入、输出和错误if (info.UseShellExecute){info.RedirectStandardOutput = false;info.RedirectStandardError = false;info.RedirectStandardInput = false;}else{info.RedirectStandardOutput = true;info.RedirectStandardError = true;info.RedirectStandardInput = true;info.StandardOutputEncoding = System.Text.UTF8Encoding.UTF8;info.StandardErrorEncoding = System.Text.UTF8Encoding.UTF8;}// 启动进程System.Diagnostics.Process process = System.Diagnostics.Process.Start(info);if (!info.UseShellExecute){Debug.Log(process.StandardOutput);Debug.Log(process.StandardError);}// 等待进程退出并关闭进程process.WaitForExit();process.Close();}
}参数说明
| 命令 | 说明 |
|---|---|
| :about | 显示关于对话框。如果没有给命令也会显示。 |
| :log | 打开日志对话框,/path 指定了显示日志的文件或目录,另外还有三个选项可以设置: /startrev:xxx、/endrev:xxx和/strict |
| :checkout | 打开检出对话框,/path指定了目标路径,而/url制定了检出的URL。 |
| :import | 打开导入对话框,/path 指定了数据导入路径。 |
| :update | 将工作副本的/path更新到HEAD,如果给定参数/rev,就会弹出一个对话框询问用户需要更新到哪个修订版本。为了防止指定修订版本号/rev:1234的对话框,需要选项/nonrecursive和/ignoreexternals。 |
| :commit | 打开提交对话框,/path 指定了目标路径或需要提交的文件列表,你也可以使用参数 /logmsg 给提交窗口传递预定义的日志信息,或者你不希望将日志传递给命令行,你也可以使用/logmsgfile:path,path 指向了保存日志信息的文件。为了预先填入bug的ID(如果你设置了集成bug追踪属性),你可以使用/bugid:"the bug id here"完成这个任务。 |
| :add | 将/path的文件添加到版本控制。 |
| :revert | 恢复工作副本的本地修改,/path说明恢复哪些条目。 |
| :cleanup | 清理中断和终止的操作,将工作副本的/path解锁。 |
| :resolve | 将/path指定文件的冲突标示为解决,如果给定/noquestion,解决不会向用户确认操作。 |
| :repocreate | 在/path创建一个版本库。 |
| :switch | 打开选项对话框。/path 指定目标目录。 |
| :export | 将/path的工作副本导出到另一个目录,如果/path指向另一个未版本控制目录,对话框会询问要导出到/path的URL。 |
| :mergeOpens | 合并对话框。/path指定目标目录。对于合并修订范围,可以使用以下选项:/fromurl:URL、/revrange:string。对于合并两个存储库树,可以使用以下选项:/fromurl:URL、/tourl:URL、/fromrev:xxx和/torev:xxx。这些预先填充合并对话框中的相关字段。 |
| :mergeall | 打开“全部合并”对话框。/path指定目标目录。 |
| :copy | 打开分支/标记对话框。/path是要从中分支/标记的工作副本。/url是目标url。您还可以指定/logmsg开关将预定义的日志消息传递到分支/标记对话框。或者,如果您不想在命令行上传递日志消息,请使用/logmsgfile:path,其中path指向包含日志消息的文件。 |
| :settings | 打开设置对话框。 |
| :remove | 从版本控制里移除/path中的文件。 |
| :rename | 重命名/path的文件,会在对话框中询问新文件,为了防止一个步骤中询问相似文件,传递/noquestion。 |
| :diff | 启动TortoiseSVN设置中指定的外部差异程序。/path指定第一个文件。如果设置了选项/path2,则diffprogram将使用这两个文件启动。如果省略/path2,则在/path中的文件与其BASE之间进行差异。要明确设置愿景编号,请使用/startrev:xxx和/endrev:xxx。如果设置了/chint而未设置/path2,则通过首先将给定的修订归咎于文件来进行差异处理。 |
| :showcompare | 根据要比较的URL和修订,这要么显示一个统一的diff(如果设置了unified选项),要么显示具有已更改文件列表的对话框,或者如果URL指向文件,则启动这两个文件的diff查看器。必须指定选项url1、url2、revision1和revision2。选项pegreview、ignorecentry、责备和统一是可选的。 |
| :conflicteditor | 使用/path中冲突文件的正确文件启动TortoiseSVN设置中指定的冲突编辑器。 |
| :relocate | 打开重定位对话框,/path指定了重定位的工作副本路径。 |
| :help | 打开帮助文件 |
| :repostatus | 打开为修改检出对话框,/path 指定了工作副本目录。 |
| :repobrowser | 启动存储库浏览器对话框,指向/path中给定的工作副本的URL,或者/path直接指向URL。另外一个选项/rev:xxx可用于指定存储库浏览器应显示的修订版。如果省略/rev:xxx,则默认为HEAD。如果/path指向URL,/projectpropertiespath:path/to/wc指定读取和使用项目属性的路径。 |
| :ignore | 将/path中的对象加入到忽略列表,也就是将这些文件添加到 svn:ignore 属性。 |
| :blame | 为 /path 选项指定的文件打开追溯对话框。如果设置了 /startrev 和 /endrev 选项,不会显示询问追溯范围对话框,直接使用这些选项中的版本号。如果设置了 /line:nnn 选项,TortoiseBlame 会显示指定行数。也支持 /ignoreeol,/ignorespaces 和 /ignoreallspaces 选项。 |
| :cat | 将/path指定的工作副本或URL的文件保存到/savepath:path,修订版本号在/revision:xxx,这样可以得到特定修订版本的文件。 |
| :createpatch | 创建/path下的补丁文件。 |
| :revisiongraph | 显示/path目录下的版本变化图。 |
| :lock | 锁定/path中给定目录中的一个文件或所有文件。将显示“锁定”对话框,以便用户可以为锁定输入注释。 |
| :unlock | 解锁/path中给定目录中的一个文件或所有文件。 |
| :rebuildiconcache | 重建窗口图标缓存。仅在窗口图标损坏的情况下使用此选项。这样做的一个副作用(无法避免)是桌面上的图标被重新排列。要取消显示消息框,请通过/noquestion。 |
| :properties | 显示 /path 给出的路径之属性对话框。 |
感谢
【unity拓展】在unity3d中集成SVN命令(非cmd方式而是打开svn界面方式)
