asp net4.0网站开发线上推广员是干什么的
其他系列文章导航
Java基础合集
数据结构与算法合集设计模式合集
多线程合集
分布式合集
ES合集
文章目录
其他系列文章导航
文章目录
前言
一、题目描述
二、题解
2.1 方法一:滑动窗口
2.2 滑动窗口解题模板
三、代码
3.1 方法一:滑动窗口
四、复杂度分析
4.1 方法一:滑动窗口
前言
这是力扣的 1004 题,难度为中等,解题方案有很多种,本文讲解我认为最奇妙的一种。
又是一道滑动窗口的典型例题,可以帮助我们巩固滑动窗口算法。
这道题很活灵活现,需要加深对题意的变相理解。
一、题目描述
给定一个二进制数组 nums 和一个整数 k,如果可以翻转最多 k 个 0 ,则返回 数组中连续 1 的最大个数 。
示例 1:
输入:nums = [1,1,1,0,0,0,1,1,1,1,0], K = 2 输出:6 解释:[1,1,1,0,0,1,1,1,1,1,1] 粗体数字从 0 翻转到 1,最长的子数组长度为 6。
示例 2:
输入:nums = [0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1], K = 3 输出:10 解释:[0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1] 粗体数字从 0 翻转到 1,最长的子数组长度为 10。
提示:
1 <= nums.length <= 105nums[i]不是0就是10 <= k <= nums.length
二、题解
2.1 方法一:滑动窗口
思路与算法:
重点:题意转换。把「最多可以把 K 个 0 变成 1,求仅包含 1 的最长子数组的长度」转换为 「找出一个最长的子数组,该子数组内最多允许有 K 个 0 」。
经过上面的题意转换,我们可知本题是求最大连续子区间,可以使用滑动窗口方法。滑动窗口的限制条件是:窗口内最多有 K 个 0。
可以使用我多次分享的滑动窗口模板解决,模板在代码之后。
首先定义四个变量:
- 左指针
- 右指针
- 最长的子串长度
- 0 的数量
代码思路:
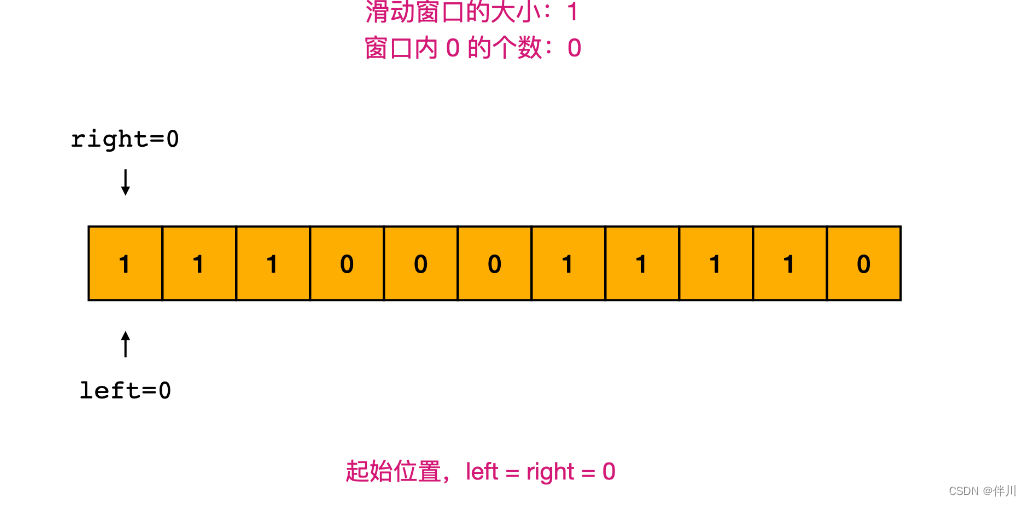
- 使用 left 和 right 两个指针,分别指向滑动窗口的左右边界。
- right 主动右移:right 指针每次移动一步。当 A[right] 为 0,说明滑动窗口内增加了一个 0;
- left 被动右移:判断此时窗口内 0 的个数,如果超过了 K,则 left 指针被迫右移,直至窗口内的 0 的个数小于等于 K 为止。
- 滑动窗口长度的最大值就是所求。
2.2 滑动窗口解题模板
滑动窗口算法是一种常用的算法,用于解决数组或列表中的子数组问题。下面是一个滑动窗口算法的解题模板:
- 定义窗口大小:首先需要确定滑动窗口的大小,即每次滑动时包含的元素个数。
- 初始化窗口:将窗口的起始位置设置为0,窗口大小设置为n,其中n为数组或列表的长度。
- 计算窗口中的元素和:使用一个变量sum来记录当前窗口中的元素和,初始值为0。
- 移动窗口:从左到右依次遍历数组或列表,每次将当前元素加入窗口中,并更新sum的值。
- 判断是否满足条件:在移动窗口的过程中,不断判断当前窗口中的元素和是否满足题目要求。如果满足条件,则返回当前窗口中的元素和。
- 移动窗口:如果当前窗口中的元素和不满足题目要求,则将窗口向右移动一位,并更新sum的值。
- 重复步骤4-6,直到遍历完整个数组或列表。
下面是一个具体的例子,使用滑动窗口算法求解数组中连续子数组的最大和:
def maxSubArray(nums): if not nums: return 0 max_sum = current_sum = nums[0] for i in range(1, len(nums)): current_sum = max(nums[i], current_sum + nums[i]) max_sum = max(max_sum, current_sum) return max_sum在这个例子中,我们使用一个变量max_sum来记录当前最大子数组的和,一个变量current_sum来记录当前窗口中的元素和。在遍历数组的过程中,不断更新current_sum的值,并判断是否满足题目要求。如果满足条件,则更新max_sum的值。最后返回max_sum即可。
三、代码
3.1 方法一:滑动窗口
Java版本:
class Solution {public int longestOnes(int[] nums, int k) {int left = 0, right = 0, longestOnes = 0, zero = 0;while (right < nums.length) {if (nums[right] == 0) zero++;if (zero > k) {left++;if (nums[left - 1] == 0) zero--;}if (zero == k || right == nums.length - 1) {longestOnes = Math.max(right - left + 1, longestOnes);}right++;}return longestOnes;}
}C++版本:
class Solution {
public:int longestOnes(vector<int>& nums, int k) {int left = 0, right = 0, longestOnes = 0, zero = 0;while (right < nums.size()) {if (nums[right] == 0) zero++;if (zero > k) {left++;if (nums[left - 1] == 0) zero--;}if (zero == k || right == nums.size() - 1) {longestOnes = max(right - left + 1, longestOnes);}right++;}return longestOnes;}
};
Python版本:
class Solution:def longestOnes(self, nums: List[int], k: int) -> int:left, right, longestOnes, zero = 0, 0, 0, 0while right < len(nums):if nums[right] == 0:zero += 1if zero > k:left += 1if nums[left - 1] == 0:zero -= 1if zero == k or right == len(nums) - 1:longestOnes = max(right - left + 1, longestOnes)right += 1return longestOnes
四、复杂度分析
4.1 方法一:滑动窗口
- 时间复杂度:O(N),因为每个元素只遍历了一次。
- 空间复杂度:O(1),因为使用了常数个空间。
