学生处网站建设工作总结百度地图手机网站开发
bat脚本
bat脚本就是DOS批处理脚本,就是将一系列DOS命令按照一定顺序排列而形成的集合,运行在windows命令行环境上。这个文件的每一行都是一条DOS命令
在命令提示下键入批处理文件的名称,或者双击该批处理文件,系统就会调用Cmd.exe来运行该文件。
bat入门案例
cmd.exe
在windows环境下,命令行程序为cmd.exe。打开方式。快捷键[ctrl+r]——》键入cmd

接着,随便输入“www”回车,如果提示 “.......不是内部或外部命令,也不是可运行的程序或批处理文件。”
这是因为在环境变量Path里面没有添加此程序的执行文件,我们只有把程序的bin目录添加到Path变量里面就可以了
例如:右键“我的电脑-属性-高级-环境变量-path,
然后在其变量值后面添加“;程序安装目录/bin”(注:在添加目录前必须添加“;”号,而且此分号必须是英文格式的)。
注释、echo和pause
rem 注释符,也可以用两个冒号代替(::)
:: 注释内容
echo 后加内容即输出该内容
会暂停批处理的执行并在屏幕上显示Press any key to continue…的提示,等待用户按任意键后继续
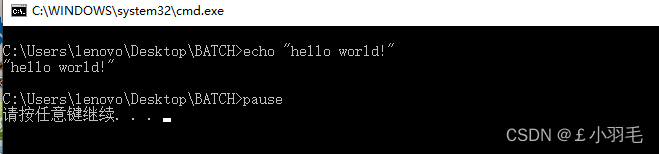
创建文件my.bat ,内容如下
:: 输出hello world echo "hello world!" pause不加pause就会:双击运行批处理文件(xxx.bat),闪一下就消失
是因为批处理运bat行完成的时间很快,需要在运行完成后给添加暂停的命令
效果
@echo off(关闭所有回显功能)
my.bat ,内容改变,在最开始加上@echo off,

双击执行该bat文件,效果如下。就没有那些乱七八糟的 盘符路径命令本身呀。。。
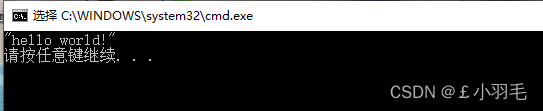
提示:pause 改为 pause>nul
可以不显示“请按任意键继续. . .”这些字,nul相当于空文件,把这些文字隐去了。
窗口color与titile
- title:设置控制台bat的标题
- color:设置bat显示的背景和前景色

试着改动一下my.bat
color 02 0代表背景色,a代表字体颜色
@echo off :: 设置窗口标题和颜色 title "bat批处理学习" color 0a echo "hello world!" pause双击执行该bat文件,效果如下
如果中文乱码,那么把bat文件的编辑改为ANSI格式
常用系统变量
%CD% 获取当前目录[盘符 + 路径]
%PATH% 获取命令搜索路径
%DATE% 获取当前日期。
%TIME% 获得系统的当前时间
%RANDOM% 获取 0 和 32767 之间的任意十进制数字。
%ERRORLEVEL% 获取上一命令执行结果码
举例,在cmd窗口中输入 echo %CD%
系统变量在bat文件中使用,如:打印当前目录和系统临时文件夹目录。
修改bat文件如下:
@echo off :: 设置窗口标题和颜色 title "bat批处理学习" color 0a echo "当前目录:"%CD% echo "系统临时文件夹目录:"%TEMP% pause
--------------------
假如你和我一样,也是乱码成这样。。。
那么把bat文件的编辑改为ANSI格式就好了
set命令
set变量:变量设置值
最普通的set命令
@echo off title "bat批处理学习" color 0a :: set命令测试 set name=小羽毛 :: 输出变量name的值 echo %name% for %%i in (*.bat) do echo %%i pause>nul双击bat文件,执行结果
set /p命令 ,让用户自己输入变量值
@echo off title "bat批处理学习" color 0a :: set命令测试 set /p num=请输入一个数字: echo 你输入的是:%num% pause>nul双击bat文件,会等待输入变量
输入姓名之后,回车
bat基础运算
算术运算
关系运算
逻辑运算
&& 短路运算
||
bat重定向运算
Handle句柄
- 句柄是Windows程序中的概念,本质是一个4字节无符号整数值,用来标示不同实例。
- 句柄是系统所管理的引用标识,该标识可以被系统重新定位到一个内存地址上。
在进程的地址空间中设一张表,表里头专门保存一些编号和由这个编号对应一个地址,而由那个地址去引用实际的对象,这个编号跟那个地址在数值上没有任何规律性的联系,纯粹是个映射而已。
在Windows系统中,这个编号就叫做"句柄"。
重定向运算>和>>和<
重定向:负责将指定命令或语句所产生的输入输出请求由缺省的“控制台”转交给其它的“设备”来完成,它的启动标志是“重定向符号”(包括“>,>>,<”三个)出现在句中。
| > | 将命令输出写入到文件或设备(例如打印机)中,而不是写在命令提示符窗口中。 |
| < | 从文件中而不是从键盘中读入命令输入。 |
| >> | 将命令输出追加到文件末尾而不删除文件中的信息。 |
dir>dirlist.txt
如果 dirlist.txt 不存在,cmd.exe 将创建该文件。如果 cirlist.txt 存在,cmd.exe 将使用 dir命令的输出替换文件中的信息。
@echo off :: if-else结构学习 title "bat批处理学习" color 0a :: 设置变量v dir>dirlist.txt type dirlist.txt pause使用type是查看文件内容的
管道运算|
| 从一个命令中读取输出并将其写入另一个命令的输入中。也称作管道。
bat流程控制
批处理是一种简单的程序,可以用 if 和 goto 来控制流程,也可以使用 for 循环。
goto 命令
流程跳转的含义是:改变默认的执行顺序,强制跳转到指定的位置执行特定的程序块。
goto [lable] 跳转到要执行的标签,在批处理中允许以“:XXX”来构建一个标号,然后用GOTO XXX跳转到标号:XXX处,然后执行标号后的命令
注意:
- 标签名必须是常量,不能是变量
- 标签必须单独一行,并且以冒号打头。
双击bat文件,结果如下:
if 命令
1.用“==” 判断字符串相等。
@echo off title "bat批处理学习" color 0a set name=李四 ::%name%是否等于"李四" if "%name%"=="李四" (echo 你是李四) else echo 你不是李四 pause>nul
2、判断数值相等。
@echo off title "bat批处理学习" color 0a set num1=15 set num2=18 :: 比较俩个数大于、等于、小于 if %num1% gtr %num2% echo %num1%大于%num2% if %num1% EQU %num2% echo %num1%等于%num2% if %num1% LSS %num2% echo %num1%小于%num2% pause>nul注意:比较运算符分为以下几种:
EQU - 等于
NEQ - 不等于
LSS - 小于
LEQ - 小于或等于
GTR - 大于
GEQ - 大于或等于
3、结合errorlevel使用
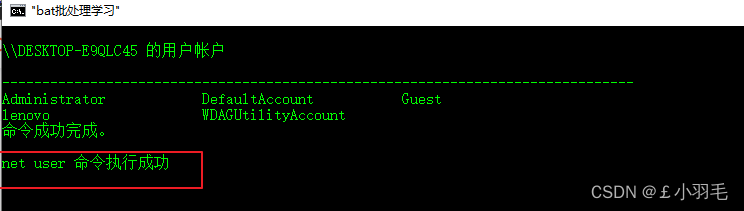
环境变量%ERRORLEVEL%包含上次执行的程序或脚本的返回码。会在执行成功时返回零,或者在执行失败时返回非零
@echo off title "bat批处理学习" color 0a net user if %ERRORLEVEL% EQU 0 echo net user 命令执行成功 pause>nul
for 命令入门使用
在批处理文件中:for %%i in (command1) do command2
for语句依次提取command1中的每一个元素,把它的值赋予形式变量i,带到do后的command2中参与命令的执行;
for语句的基本要素:
- for、in和do是for语句的关键字;
- %%i是for语句中对形式变量的引用;%%I和%%i会被认为不是同一个变量
- in之后,do之前的括号不能省略;
- command1表示字符串或变量,command2表示字符串、变量或命令语句;
for循环,后面的多个元素逗号分割(默认以空格,;三种符号分隔开)
@echo off title "bat批处理学习" color 0a :: for命令测试 for %%i in (www,baidu,com) do echo %%i pause>nul执行结果
*.*,显示当前目录下所有的文件名
@echo off title "bat批处理学习" color 0a :: for命令测试 echo 显示当前目录下所有的文件名 for %%i in (*.*) do echo %%i pause>nul双击bat文件,执行结果
*.bat,显示当前目录下以.bat结尾的文件
@echo off title "bat批处理学习" color 0a :: for命令测试 echo 显示当前目录下以.bat结尾的文件 for %%i in (*.bat) do echo %%i pause>nul双击bat文件,执行结果
for 命令参数扩展
start命令
启动单独的“命令提示符”窗口来运行指定程序或命令。
用法:可以打开盘符、文件、文件夹、网址、程序...
start打开盘符
@echo off title "bat批处理学习" color 0a :: set命令测试 start e: pause>nul打开时,可以指定最大化、最小化
------------------------
start打开文件夹
:: 最小化方式打开文件夹 start /min e:\PR最小化,就是可以在任务栏找到啦
------------------------
start打开文件
:: 打开文件 start c:\aow_drv.log---------------------
start 打开网址
:: 使用默认浏览器打开网址 start https://mp.csdn.net---------------------
start 打开应用程序
:: 打开应用程序 start D:\tools\IntelliJ IDEA 2019.2.2\bin\idea64.exe额,会报错。是因为路径中有空格
可以这么用双引号,这么改
:: 打开应用程序 start D:\tools\"IntelliJ IDEA 2019.2.2"\bin\idea64.exe
call命令
Dos命令
文件夹和文件
目录的查看、创建和删除
mkdir [目录名] 新建目录
如:
mkdir test
创建多级目录?
rmdir [目录名] 目录删除
如:删除刚刚新建的test目录
rmdir test
目录切换cd
只切换盘符,此时不需要cd ,直接"d:"字母大小写都可以。
格式:cd+空格+要切换的目录
结果就很尴尬了,,,为啥没切换成功呢?
方法一:因为要先切换盘符啊
方法二(推荐):
当然也可以在cd 和路径中间 增加一个'/d'
windows下路径分为:绝对路径和相对路径
绝对路径:在windows操作系统中凡是路径起点是盘符的都是绝对路径
相对路径:相对路径是相对于当前位置而言,以当前所在的位置作为起点。
切换到上级目录:cd ..
切换到根目录:cd \
type查看文件内容