济南高新网站建设网站提交做外链有什么作用
提及笔记,不少人都会和学习挂钩,的确学习过程中我们经常会遇到很多难题,而经常记录笔记可以有效地帮助大家记住很多知识,而且时常拿出笔记查看一下,可方便巩固过去学习的知识。
手机作为大家日常随身携带的工具,可以借助一些手机电子笔记工具来整理学习笔记,手机上适合记录学习笔记的工具选择哪一个呢?今天给大家介绍一款比较好用的笔记工具:敬业签,其可以在iPhone手机、Android手机、HarmonyOS手机系统使用,可方便大家快速记录学习笔记。

在整理学习笔记时,推荐大家使用敬业签的便签分类,便签分类可以让记录的笔记内容更加多元化,其不仅可添加文字记录,同时还支持添加图片、录入声音、以文档/表格/视频/音频等形式上传附件等,在创建分类时支持创建50个分类,每一个分类下可容纳1000条便签内容,每一个便签均相当于一个小网盘,不仅存储容量大,而且存储形式也多样化。
选择用手机便签添加笔记记录,大家可以随时掏出手机查看笔记内容,便于复习和回顾知识点;倘若笔记内容比较多时,大家还可以选择使用软件的内容搜索功能,输入关键词查询相关的学习笔记。
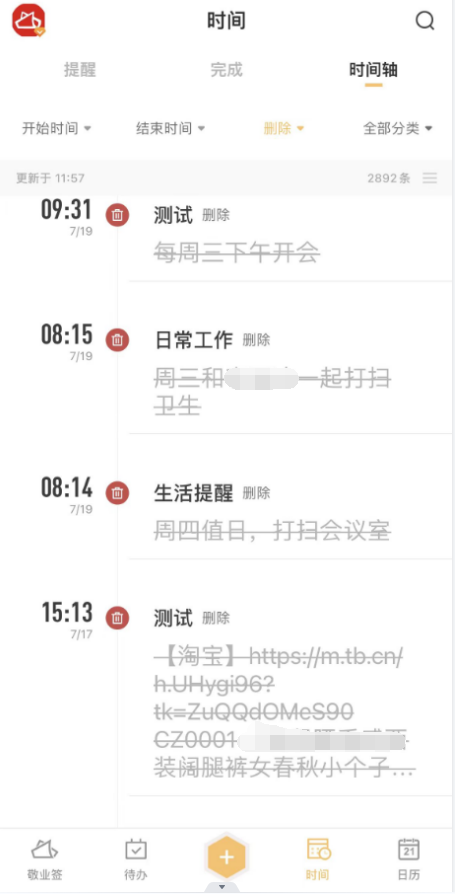
另外,敬业签还有一个日志时间轴功能,可以存储备份大家每次在便签上新增、修改、删除的内容,当记录的学习笔记不小心误删或者编辑后仍旧想要查看先前的记录时,大家可以从时间轴中快捷找回。
记录学习笔记想要找寻好用的电子笔记时,大家可来关注下敬业签软件,敬业签是一款云端存储的便签工具,可辅助大家记录许多学习笔记内容,快来体验下吧~
