代理网站备案wordpress怎么做分页
末尾获取源码
开发语言:Java
Java开发工具:JDK1.8
后端框架:SSM
前端:采用JSP技术开发
数据库:MySQL5.7和Navicat管理工具结合
服务器:Tomcat8.5
开发软件:IDEA / Eclipse
是否Maven项目:是
目录
一、项目简介
二、系统功能
三、系统项目截图
医生信息管理
护士信息管理
患者信息管理
病房信息管理
门诊病历管理
住院病历管理
药品信息管理
公告信息管理
四、核心代码
登录相关
文件上传
封装
一、项目简介
随着信息技术在管理上越来越深入而广泛的应用,管理信息系统的实施在技术上已逐步成熟。本文介绍了电子病历系统的开发全过程。通过分析电子病历系统方面的不足,创建了一个计算机管理电子病历系统的方案。文章介绍了电子病历系统的系统分析部分,包括可行性分析等,系统设计部分主要介绍了系统功能设计和数据库设计。
本电子病历系统有管理员,护士,门诊医生,住院医生。
管理员功能有个人中心,医生管理,护士管理,患者管理,病房管理,门诊病历管理,住院病历管理,药品管理,公告管理,基础数据管理等。
门诊医生功能有个人中心,患者管理,病房管理,门诊病历管理,药品管理,公告管理等。
护士功能有有个人中心,患者管理,病房管理,门诊病历管理,药品管理,住院病历管理,公告管理等。
住院医生功能有个人中心,患者管理,药房管理,病房管理,住院病历管理,药品管理,公告管理等。因而具有一定的实用性。
本站是一个B/S模式系统,采用SSM框架,MYSQL数据库设计开发,充分保证系统的稳定性。系统具有界面清晰、操作简单,功能齐全的特点,使得电子病历系统管理工作系统化、规范化。
关键词:电子病历系统;SSM框架;MYSQL数据库
二、系统功能
本系统是基于B/S架构的网站系统,设计的功能结构图如下图所示:
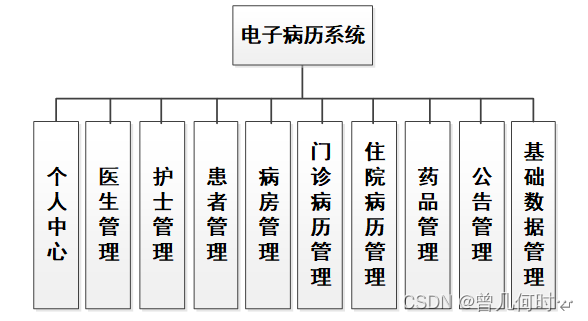
三、系统项目截图
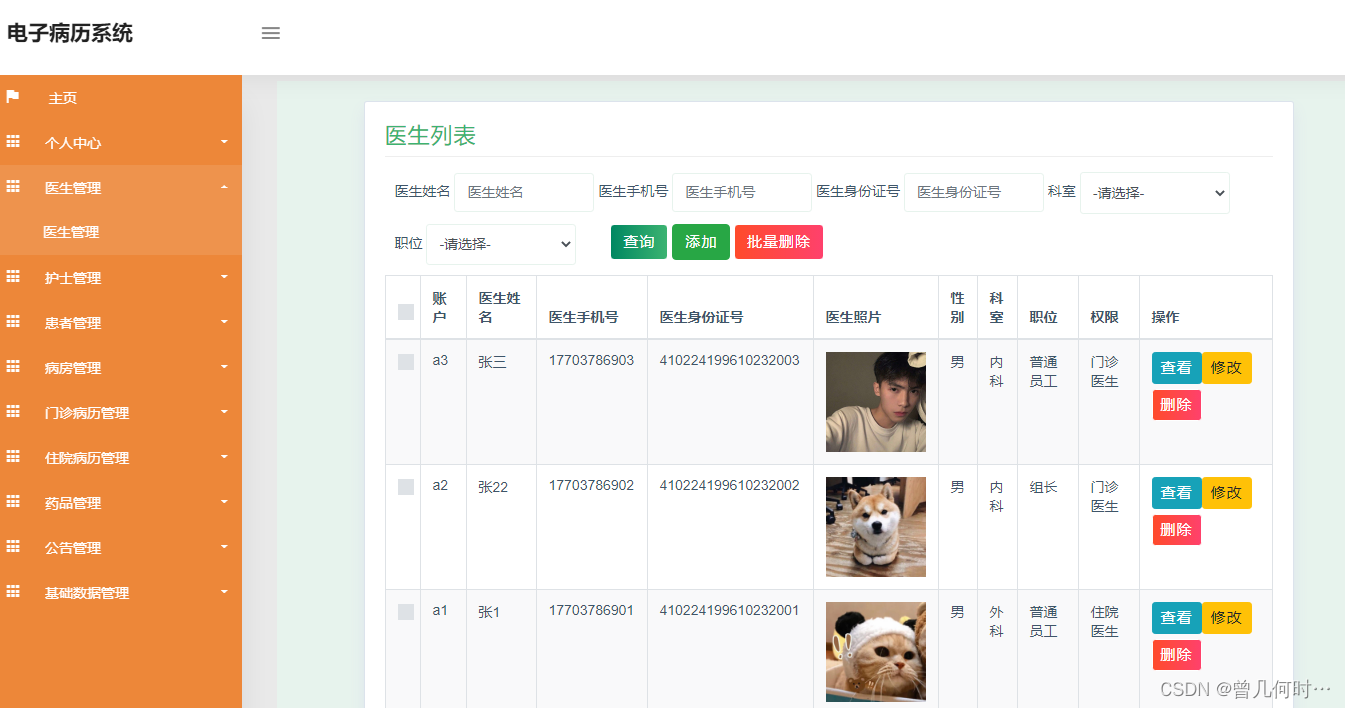
医生信息管理
电子病历系统的系统管理员可以对医生信息添加修改删除以及查询操作。
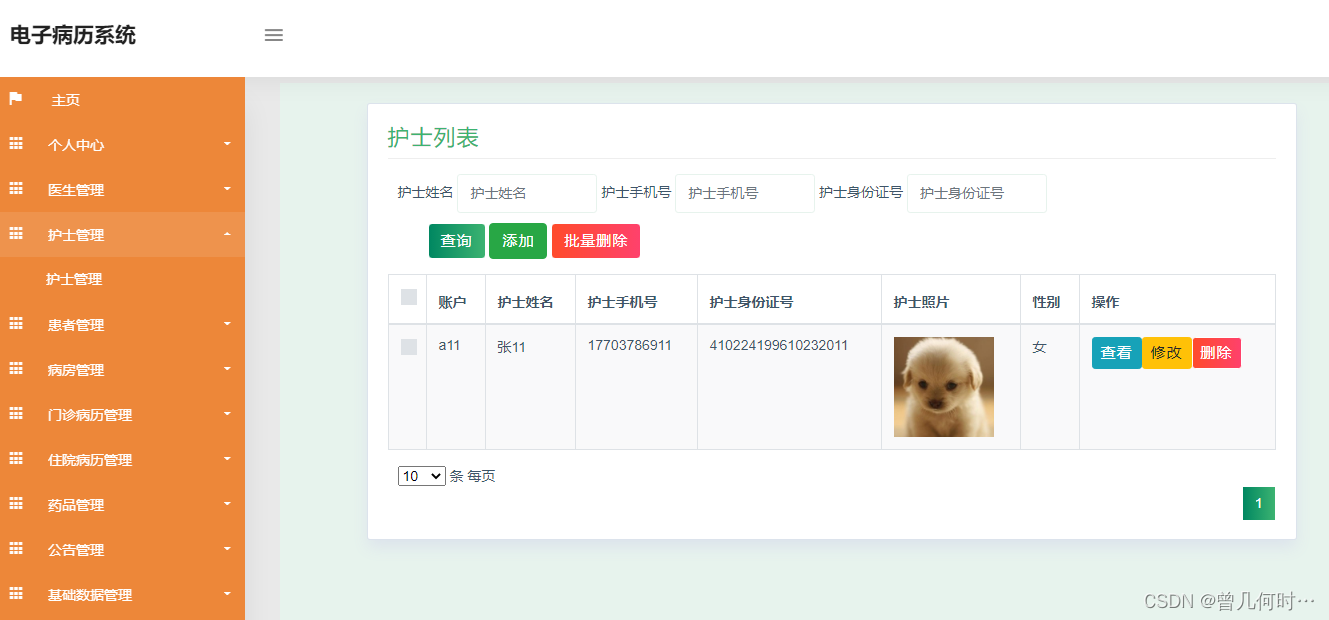
护士信息管理
系统管理员可以查看对护士信息进行添加,修改,删除以及查询操作。
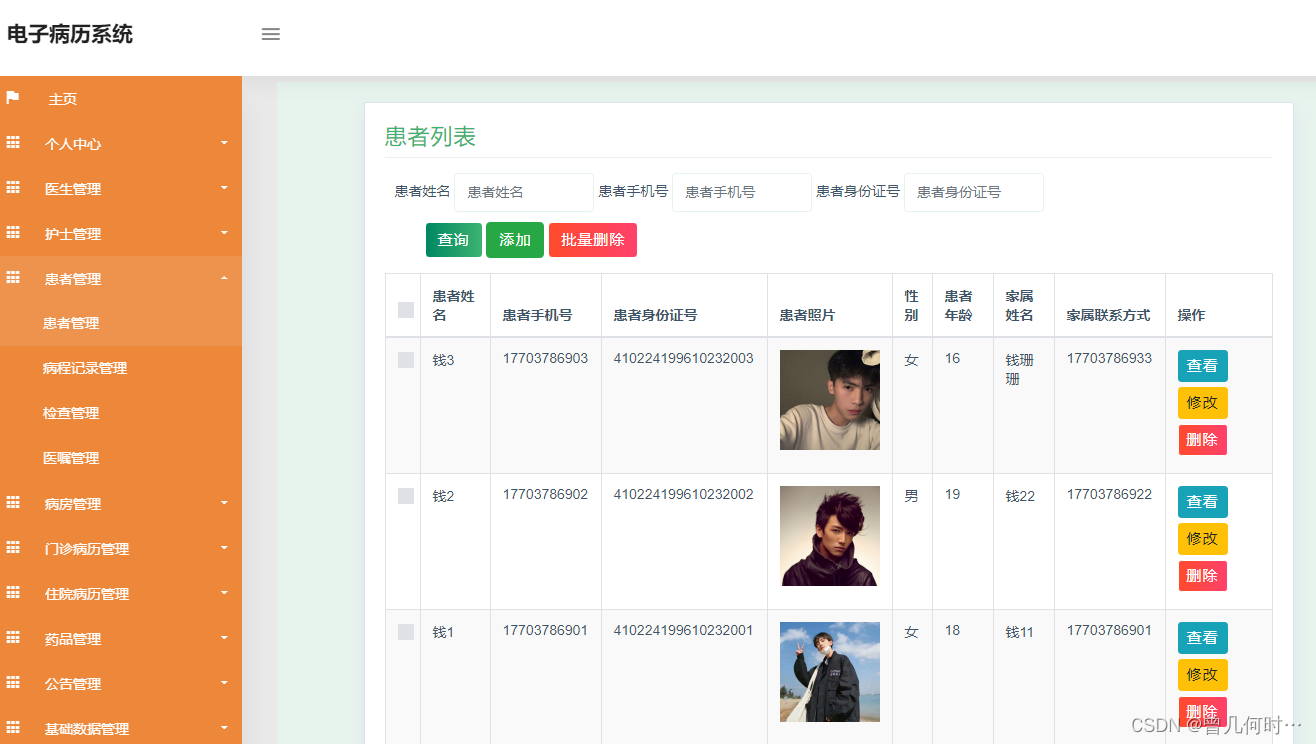
患者信息管理
系统管理员可以查看对患者信息进行添加,修改,删除以及查询操作。
病房信息管理
系统管理员可以查看对病房信息进行添加,修改,删除以及查询操作。
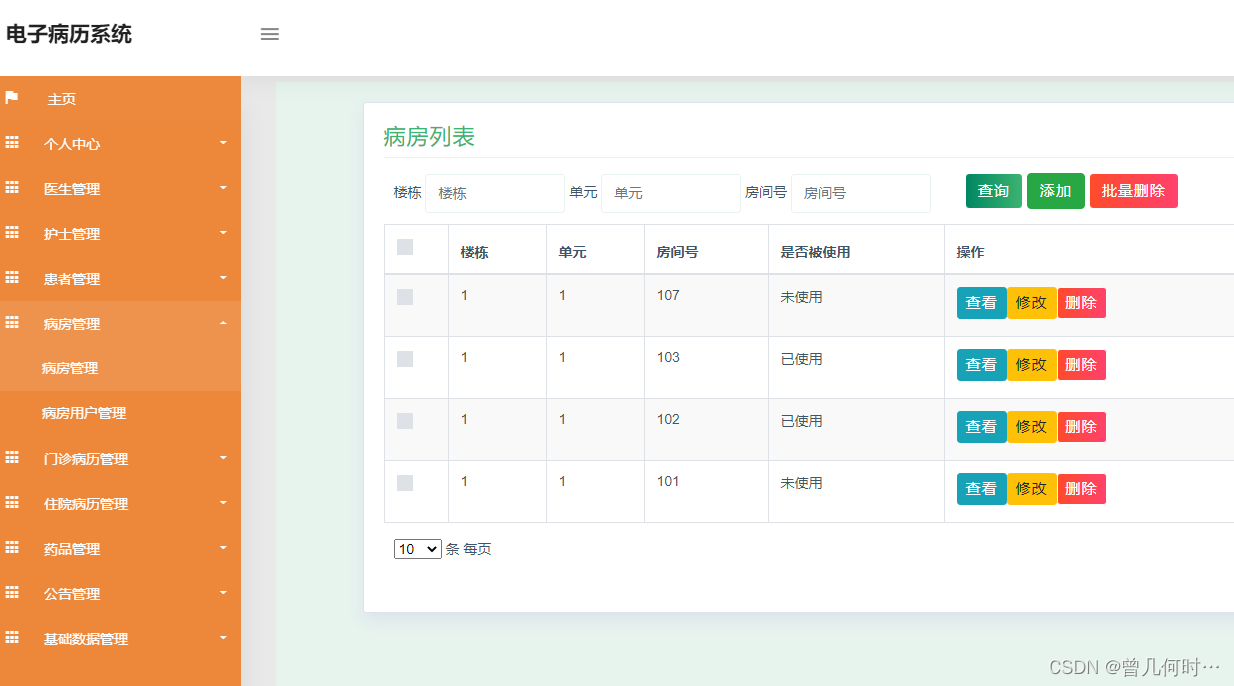
门诊病历管理
系统管理员可以查看对门诊病历进行添加,修改,删除以及查询操作。
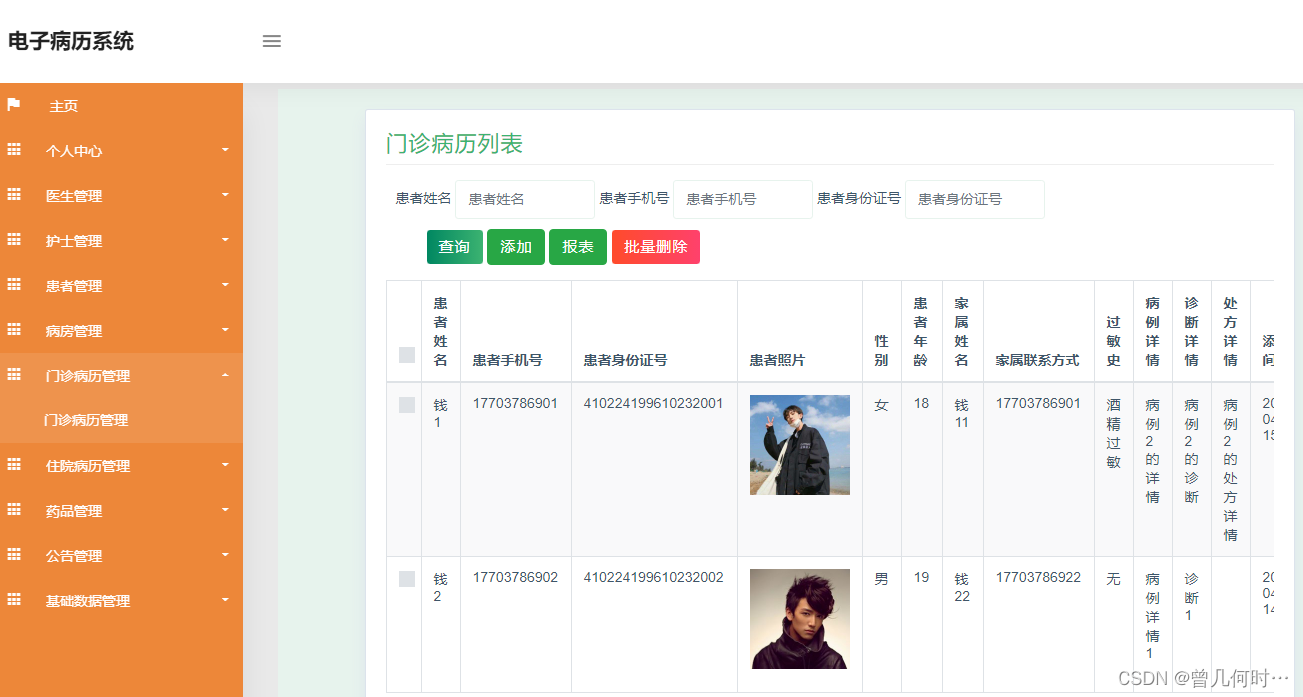
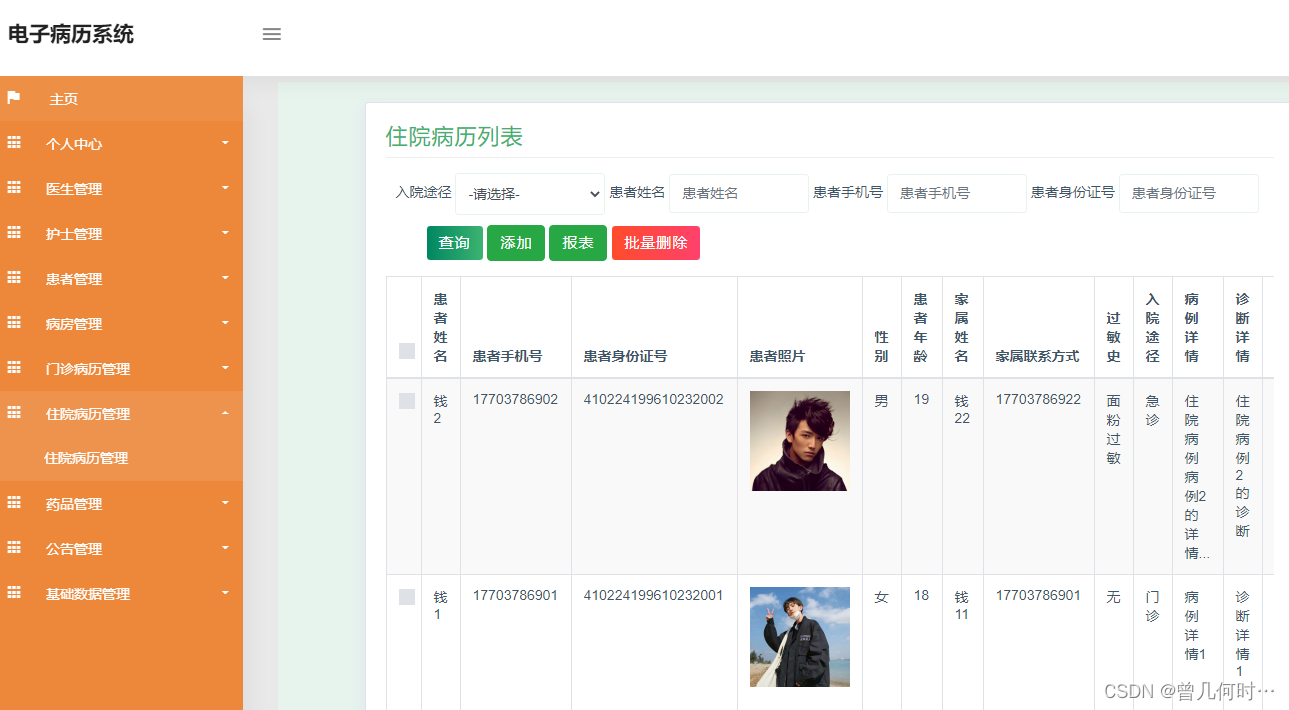
住院病历管理
系统管理员可以查看对住院病历进行添加,修改,删除以及查询操作。
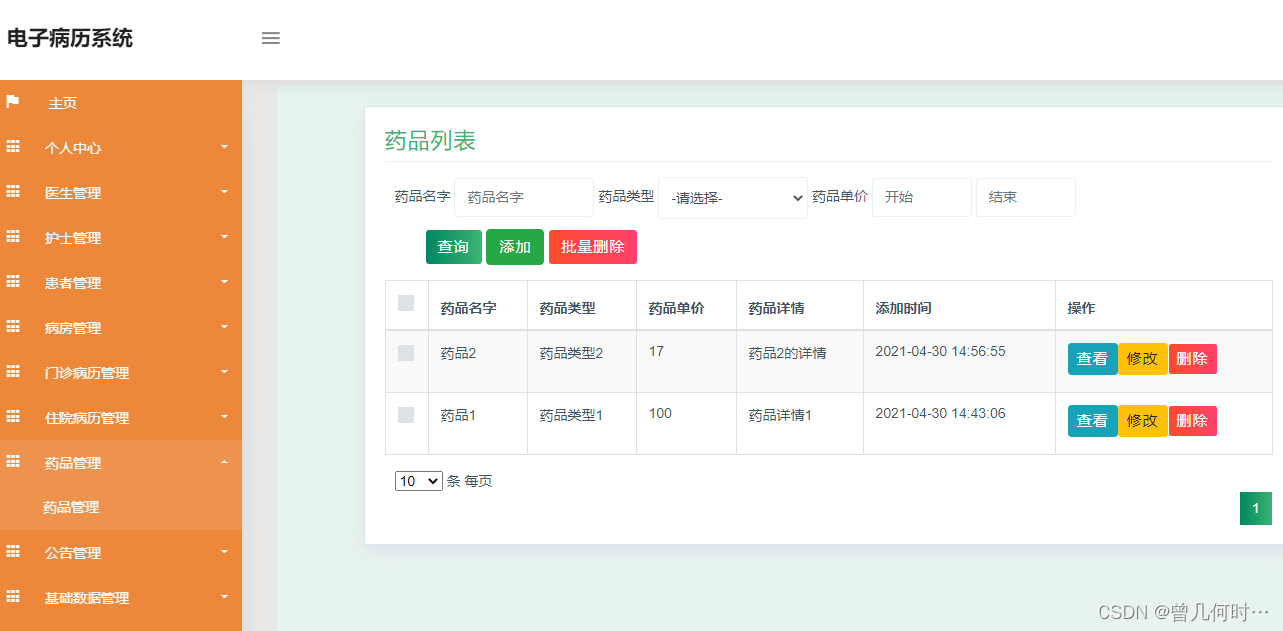
药品信息管理
管理员可以对药品信息进行添加,修改,删除以及查询操作。
公告信息管理
管理员可以对公告信息进行添加,修改,删除,查询操作。
四、核心代码
登录相关
package com.controller;import java.util.Arrays;
import java.util.Calendar;
import java.util.Date;
import java.util.Map;import javax.servlet.http.HttpServletRequest;import org.springframework.beans.factory.annotation.Autowired;
import org.springframework.stereotype.Controller;
import org.springframework.web.bind.annotation.GetMapping;
import org.springframework.web.bind.annotation.PathVariable;
import org.springframework.web.bind.annotation.PostMapping;
import org.springframework.web.bind.annotation.RequestBody;
import org.springframework.web.bind.annotation.RequestMapping;
import org.springframework.web.bind.annotation.RequestParam;
import org.springframework.web.bind.annotation.ResponseBody;
import org.springframework.web.bind.annotation.RestController;import com.annotation.IgnoreAuth;
import com.baomidou.mybatisplus.mapper.EntityWrapper;
import com.entity.TokenEntity;
import com.entity.UserEntity;
import com.service.TokenService;
import com.service.UserService;
import com.utils.CommonUtil;
import com.utils.MD5Util;
import com.utils.MPUtil;
import com.utils.PageUtils;
import com.utils.R;
import com.utils.ValidatorUtils;/*** 登录相关*/
@RequestMapping("users")
@RestController
public class UserController{@Autowiredprivate UserService userService;@Autowiredprivate TokenService tokenService;/*** 登录*/@IgnoreAuth@PostMapping(value = "/login")public R login(String username, String password, String captcha, HttpServletRequest request) {UserEntity user = userService.selectOne(new EntityWrapper<UserEntity>().eq("username", username));if(user==null || !user.getPassword().equals(password)) {return R.error("账号或密码不正确");}String token = tokenService.generateToken(user.getId(),username, "users", user.getRole());return R.ok().put("token", token);}/*** 注册*/@IgnoreAuth@PostMapping(value = "/register")public R register(@RequestBody UserEntity user){
// ValidatorUtils.validateEntity(user);if(userService.selectOne(new EntityWrapper<UserEntity>().eq("username", user.getUsername())) !=null) {return R.error("用户已存在");}userService.insert(user);return R.ok();}/*** 退出*/@GetMapping(value = "logout")public R logout(HttpServletRequest request) {request.getSession().invalidate();return R.ok("退出成功");}/*** 密码重置*/@IgnoreAuth@RequestMapping(value = "/resetPass")public R resetPass(String username, HttpServletRequest request){UserEntity user = userService.selectOne(new EntityWrapper<UserEntity>().eq("username", username));if(user==null) {return R.error("账号不存在");}user.setPassword("123456");userService.update(user,null);return R.ok("密码已重置为:123456");}/*** 列表*/@RequestMapping("/page")public R page(@RequestParam Map<String, Object> params,UserEntity user){EntityWrapper<UserEntity> ew = new EntityWrapper<UserEntity>();PageUtils page = userService.queryPage(params, MPUtil.sort(MPUtil.between(MPUtil.allLike(ew, user), params), params));return R.ok().put("data", page);}/*** 列表*/@RequestMapping("/list")public R list( UserEntity user){EntityWrapper<UserEntity> ew = new EntityWrapper<UserEntity>();ew.allEq(MPUtil.allEQMapPre( user, "user")); return R.ok().put("data", userService.selectListView(ew));}/*** 信息*/@RequestMapping("/info/{id}")public R info(@PathVariable("id") String id){UserEntity user = userService.selectById(id);return R.ok().put("data", user);}/*** 获取用户的session用户信息*/@RequestMapping("/session")public R getCurrUser(HttpServletRequest request){Long id = (Long)request.getSession().getAttribute("userId");UserEntity user = userService.selectById(id);return R.ok().put("data", user);}/*** 保存*/@PostMapping("/save")public R save(@RequestBody UserEntity user){
// ValidatorUtils.validateEntity(user);if(userService.selectOne(new EntityWrapper<UserEntity>().eq("username", user.getUsername())) !=null) {return R.error("用户已存在");}userService.insert(user);return R.ok();}/*** 修改*/@RequestMapping("/update")public R update(@RequestBody UserEntity user){
// ValidatorUtils.validateEntity(user);userService.updateById(user);//全部更新return R.ok();}/*** 删除*/@RequestMapping("/delete")public R delete(@RequestBody Long[] ids){userService.deleteBatchIds(Arrays.asList(ids));return R.ok();}
}
文件上传
package com.controller;import java.io.File;
import java.io.FileNotFoundException;
import java.io.IOException;
import java.util.Arrays;
import java.util.Date;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
import java.util.Random;
import java.util.UUID;import org.apache.commons.io.FileUtils;
import org.apache.commons.lang3.StringUtils;
import org.springframework.beans.factory.annotation.Autowired;
import org.springframework.http.HttpHeaders;
import org.springframework.http.HttpStatus;
import org.springframework.http.MediaType;
import org.springframework.http.ResponseEntity;
import org.springframework.util.ResourceUtils;
import org.springframework.web.bind.annotation.PathVariable;
import org.springframework.web.bind.annotation.RequestBody;
import org.springframework.web.bind.annotation.RequestMapping;
import org.springframework.web.bind.annotation.RequestParam;
import org.springframework.web.bind.annotation.RestController;
import org.springframework.web.multipart.MultipartFile;import com.annotation.IgnoreAuth;
import com.baomidou.mybatisplus.mapper.EntityWrapper;
import com.entity.ConfigEntity;
import com.entity.EIException;
import com.service.ConfigService;
import com.utils.R;/*** 上传文件映射表*/
@RestController
@RequestMapping("file")
@SuppressWarnings({"unchecked","rawtypes"})
public class FileController{@Autowiredprivate ConfigService configService;/*** 上传文件*/@RequestMapping("/upload")public R upload(@RequestParam("file") MultipartFile file,String type) throws Exception {if (file.isEmpty()) {throw new EIException("上传文件不能为空");}String fileExt = file.getOriginalFilename().substring(file.getOriginalFilename().lastIndexOf(".")+1);File path = new File(ResourceUtils.getURL("classpath:static").getPath());if(!path.exists()) {path = new File("");}File upload = new File(path.getAbsolutePath(),"/upload/");if(!upload.exists()) {upload.mkdirs();}String fileName = new Date().getTime()+"."+fileExt;File dest = new File(upload.getAbsolutePath()+"/"+fileName);file.transferTo(dest);FileUtils.copyFile(dest, new File("C:\\Users\\Desktop\\jiadian\\springbootl7own\\src\\main\\resources\\static\\upload"+"/"+fileName));if(StringUtils.isNotBlank(type) && type.equals("1")) {ConfigEntity configEntity = configService.selectOne(new EntityWrapper<ConfigEntity>().eq("name", "faceFile"));if(configEntity==null) {configEntity = new ConfigEntity();configEntity.setName("faceFile");configEntity.setValue(fileName);} else {configEntity.setValue(fileName);}configService.insertOrUpdate(configEntity);}return R.ok().put("file", fileName);}/*** 下载文件*/@IgnoreAuth@RequestMapping("/download")public ResponseEntity<byte[]> download(@RequestParam String fileName) {try {File path = new File(ResourceUtils.getURL("classpath:static").getPath());if(!path.exists()) {path = new File("");}File upload = new File(path.getAbsolutePath(),"/upload/");if(!upload.exists()) {upload.mkdirs();}File file = new File(upload.getAbsolutePath()+"/"+fileName);if(file.exists()){/*if(!fileService.canRead(file, SessionManager.getSessionUser())){getResponse().sendError(403);}*/HttpHeaders headers = new HttpHeaders();headers.setContentType(MediaType.APPLICATION_OCTET_STREAM); headers.setContentDispositionFormData("attachment", fileName); return new ResponseEntity<byte[]>(FileUtils.readFileToByteArray(file),headers, HttpStatus.CREATED);}} catch (IOException e) {e.printStackTrace();}return new ResponseEntity<byte[]>(HttpStatus.INTERNAL_SERVER_ERROR);}}
封装
package com.utils;import java.util.HashMap;
import java.util.Map;/*** 返回数据*/
public class R extends HashMap<String, Object> {private static final long serialVersionUID = 1L;public R() {put("code", 0);}public static R error() {return error(500, "未知异常,请联系管理员");}public static R error(String msg) {return error(500, msg);}public static R error(int code, String msg) {R r = new R();r.put("code", code);r.put("msg", msg);return r;}public static R ok(String msg) {R r = new R();r.put("msg", msg);return r;}public static R ok(Map<String, Object> map) {R r = new R();r.putAll(map);return r;}public static R ok() {return new R();}public R put(String key, Object value) {super.put(key, value);return this;}
}
