创造一个网站白领兼职做网站
1.首先在postman新建要批量运行的接口文件夹,新建一个接口,并设置好全局变量。
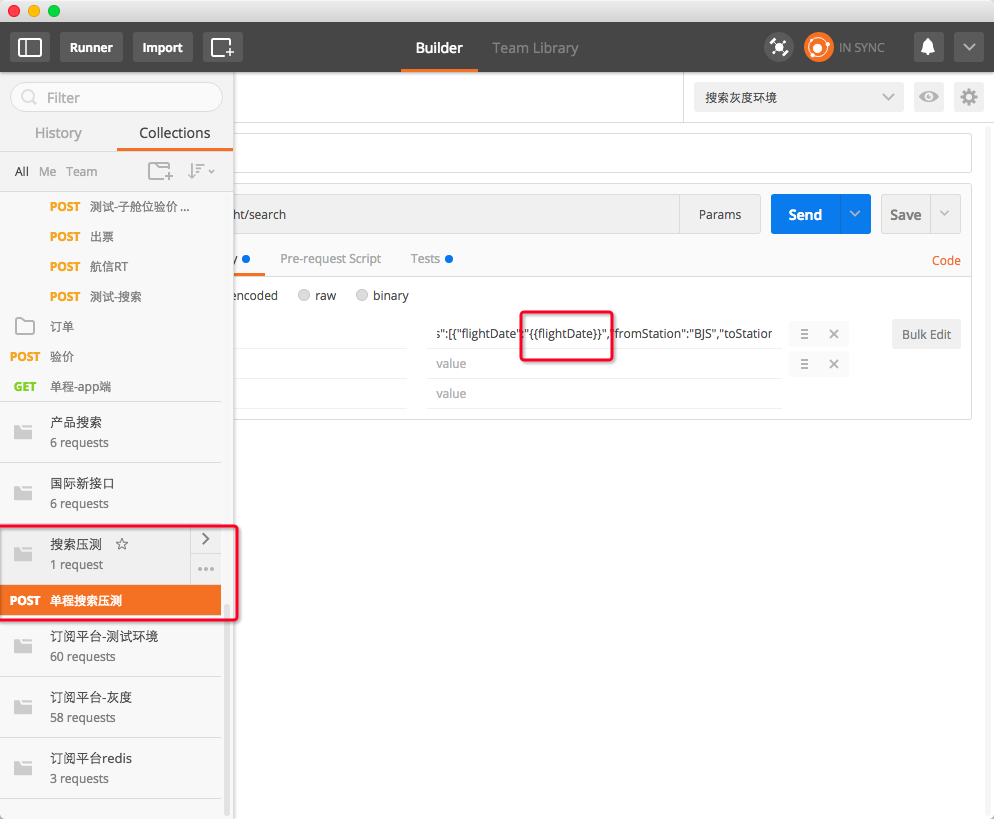
2.然后在Test里面设置好要断言的方法
如:
tests["Status code is 200"] = responseCode.code === 200;
tests["Response time is less than 10000ms"] = responseTime < 10000;
console.log(responseTime);
3.保存后,点击Runner,选择刚才新建的文件夹,设置好迭代和测试环境
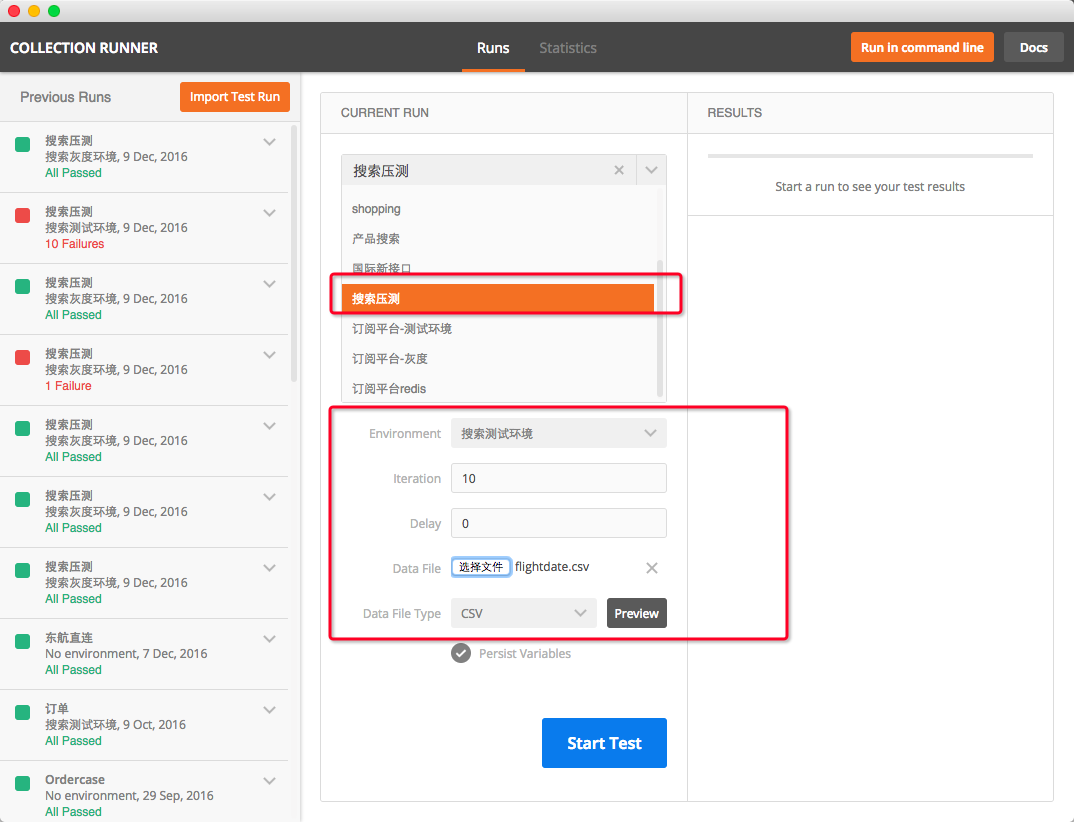
4.步骤一中设置的接口全局变量是flightdate,我们在每次迭代中给这个变量赋值,就需要用到csv或者json文件,如我用的json文件。
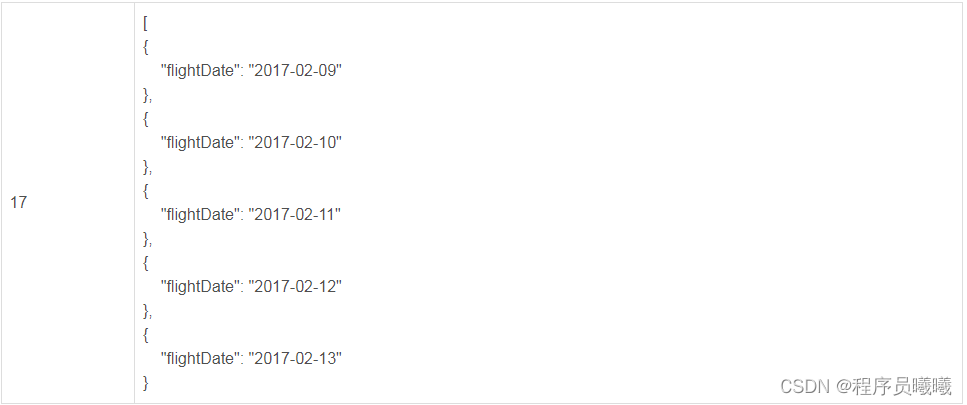
注意:json的key一定要与变量名一致,json的格式是数组形式
5.在Runner中选择该json文件,点击预览效果:
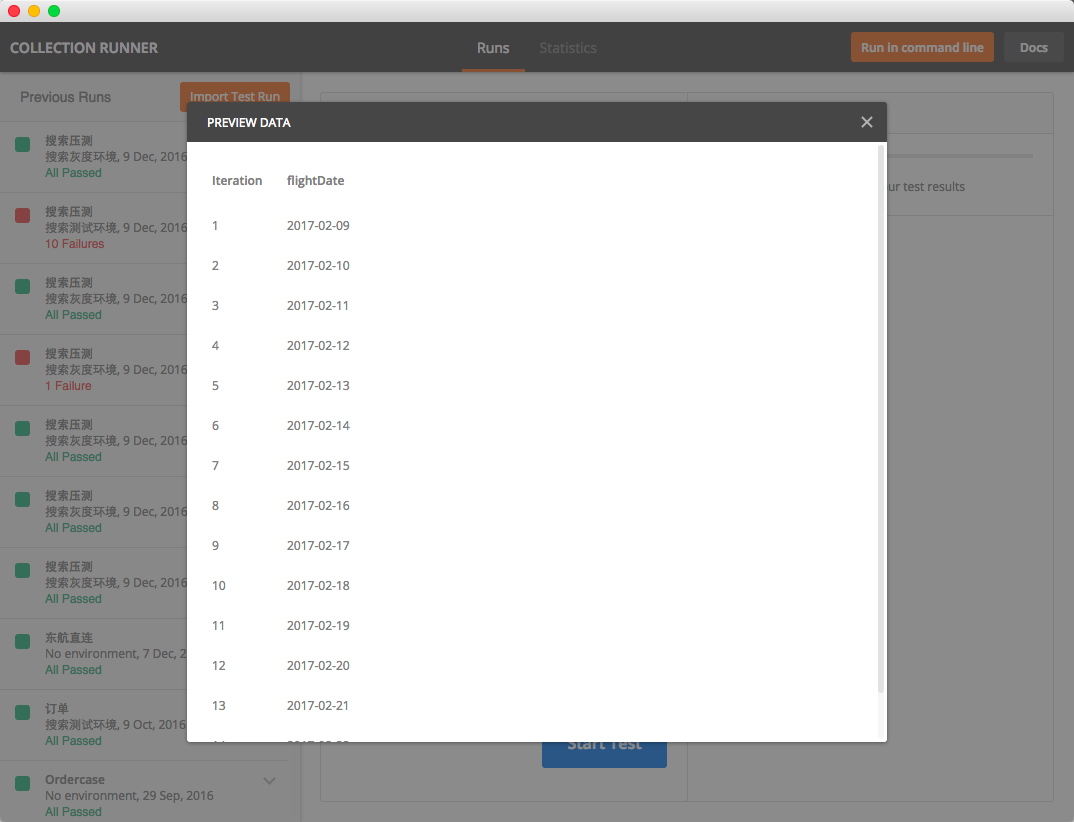
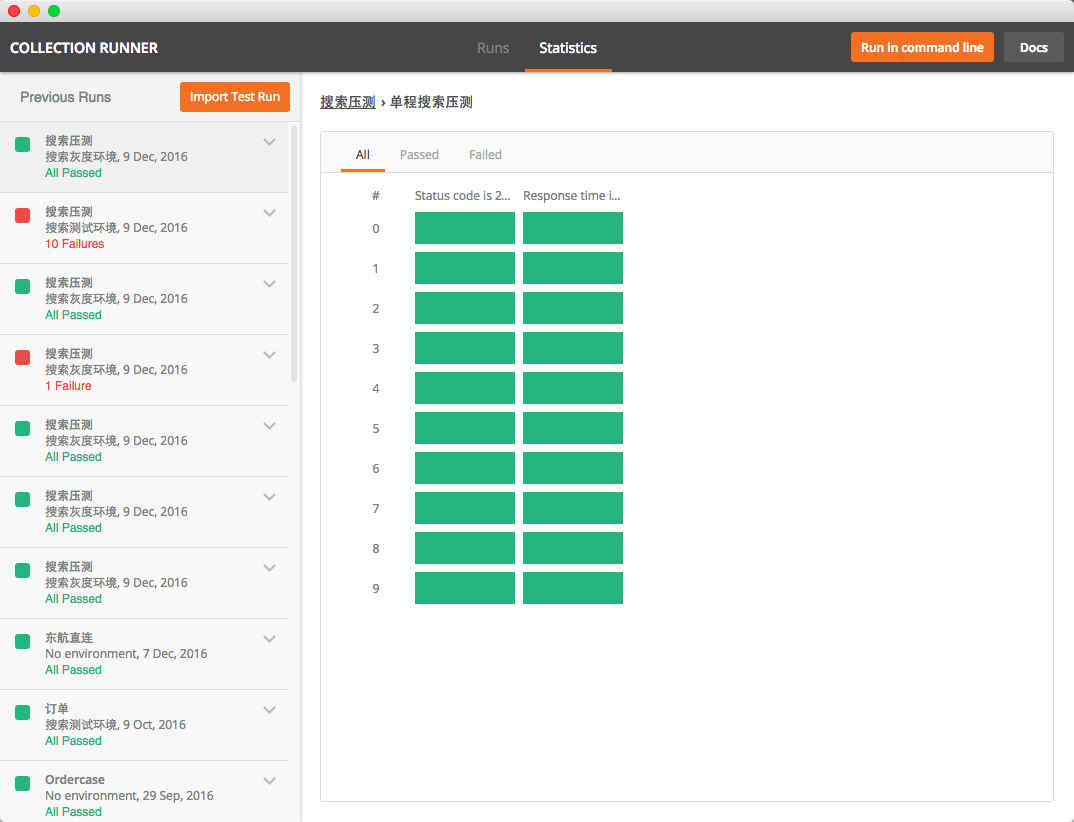
6.配置好后,点击start test,即可看到运行结果。
最后感谢每一个认真阅读我文章的人,礼尚往来总是要有的,虽然不是什么很值钱的东西,如果你用得到的话可以直接拿走:
软件测试面试小程序
被百万人刷爆的软件测试题库!!!谁用谁知道!!!全网最全面试刷题小程序,手机就可以刷题,地铁上公交上,卷起来!
涵盖以下这些面试题板块:
1、软件测试基础理论 ,2、web,app,接口功能测试 ,3、网络 ,4、数据库 ,5、linux
6、web,app,接口自动化 ,7、性能测试 ,8、编程基础,9、hr面试题 ,10、开放性测试题,11、安全测试,12、计算机基础

这些资料,对于【软件测试】的朋友来说应该是最全面最完整的备战仓库,这个仓库也陪伴上万个测试工程师们走过最艰难的路程,希望也能帮助到你!

