国外优秀购物网站设计铜仁网站建设
需求
我们有时会用到一些dll,需要把这些dll和我们生成的exe放到一起,一般我们是手动自己copy,
这样发布的时候,有时会忘记拷贝这个dll,导致程序运行出错。学会这个小技巧,就能实现自动copy,非常简单。
具体步骤
首先右键当前项目,找到整成标签下的事件标签,然后在生成事件后这里,写上:
copy "..\dll\libxl.dll" $(TargetDir)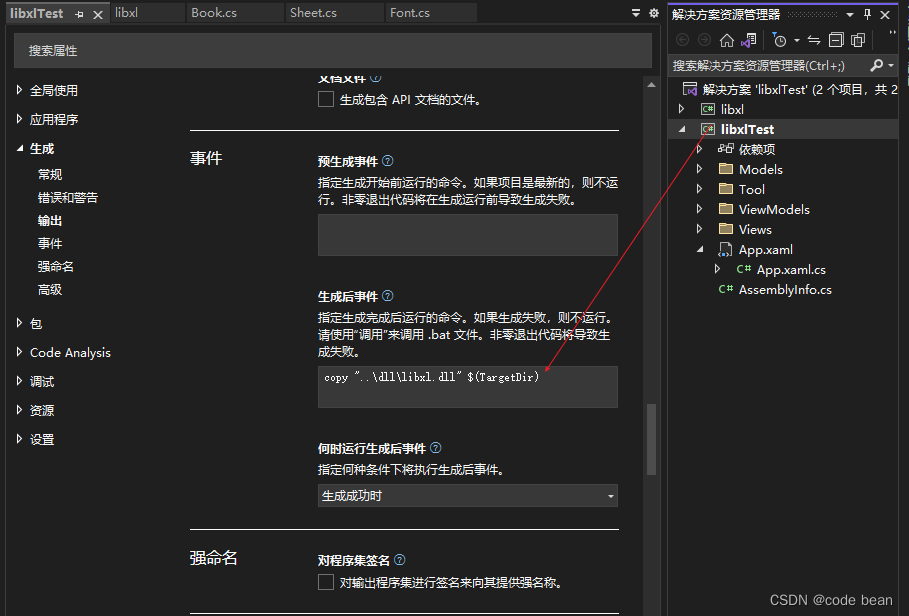
copy "..\dll\libxl.dll" $(TargetDir) 相当于执行一句脚本命令!
意思就把libxl.dll 拷贝到 $(TargetDir) “TargetDir” 这变量就表示exe的输出路径。$(TargetDir)表示取出变量“TargetDir”中的值。
这里 "..\dll\libxl.dll" 使用的是相对路径,当然你可以使用绝对路径。这里当前路径就是当前子项目的路径。
..\ 就是解决方案的路径,..\dll就是解决方案下一个dll 文件夹,在这个文件夹里有个libxl.dll,在编译完成之后,就会把libxl.dll拷贝到 $(TargetDir) ! 就这么简单。
