在建设部网站首页网站盈利模式设计
Open WebUI 是一个扩展性强、功能丰富且用户友好的自托管 WebUI,旨在完全离线操作。它支持各种 LLM 服务,包括 Ollama 和 OpenAI 兼容的 API。该项目在 GitHub 上已有 38k 星,非常受欢迎。
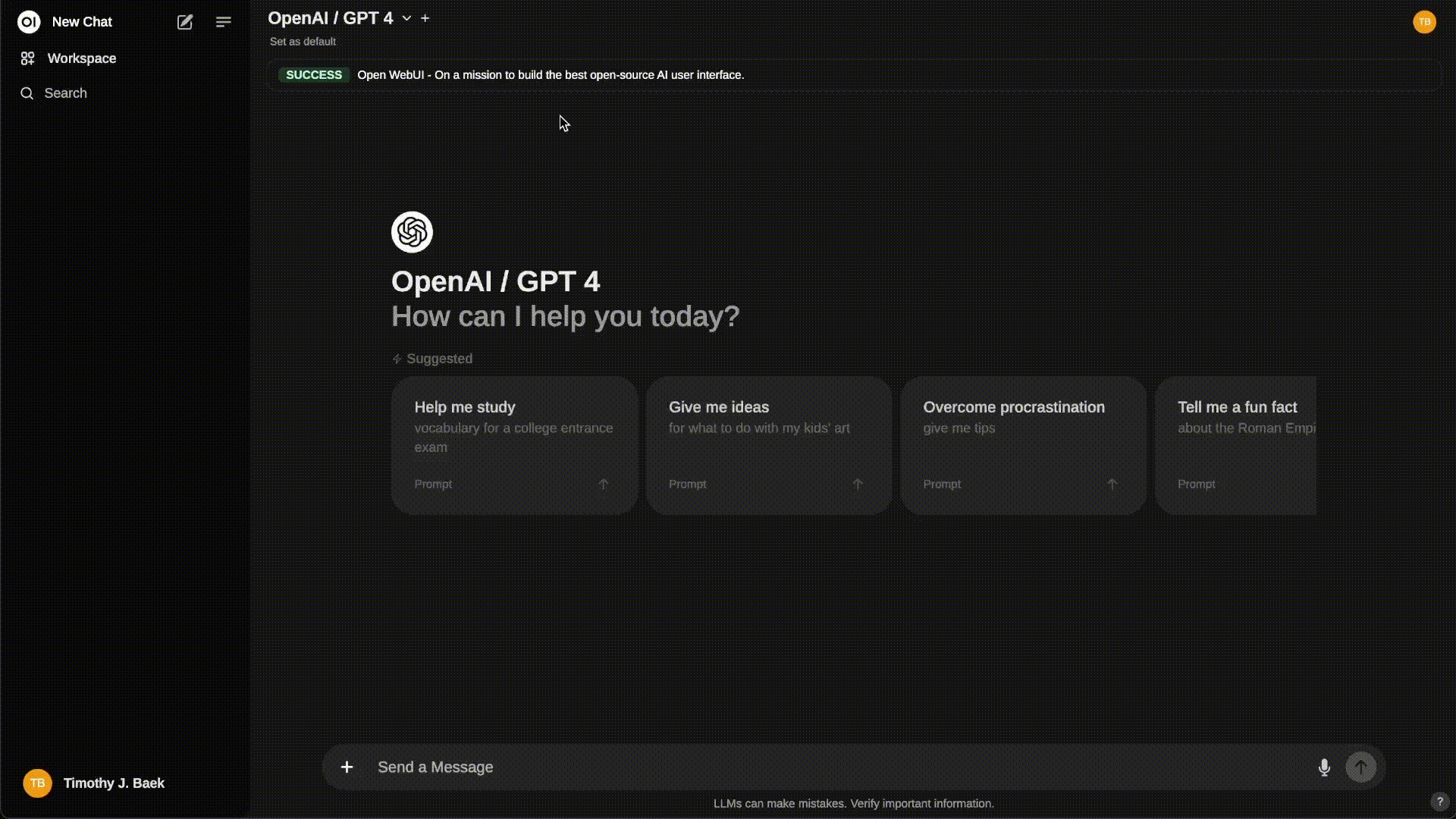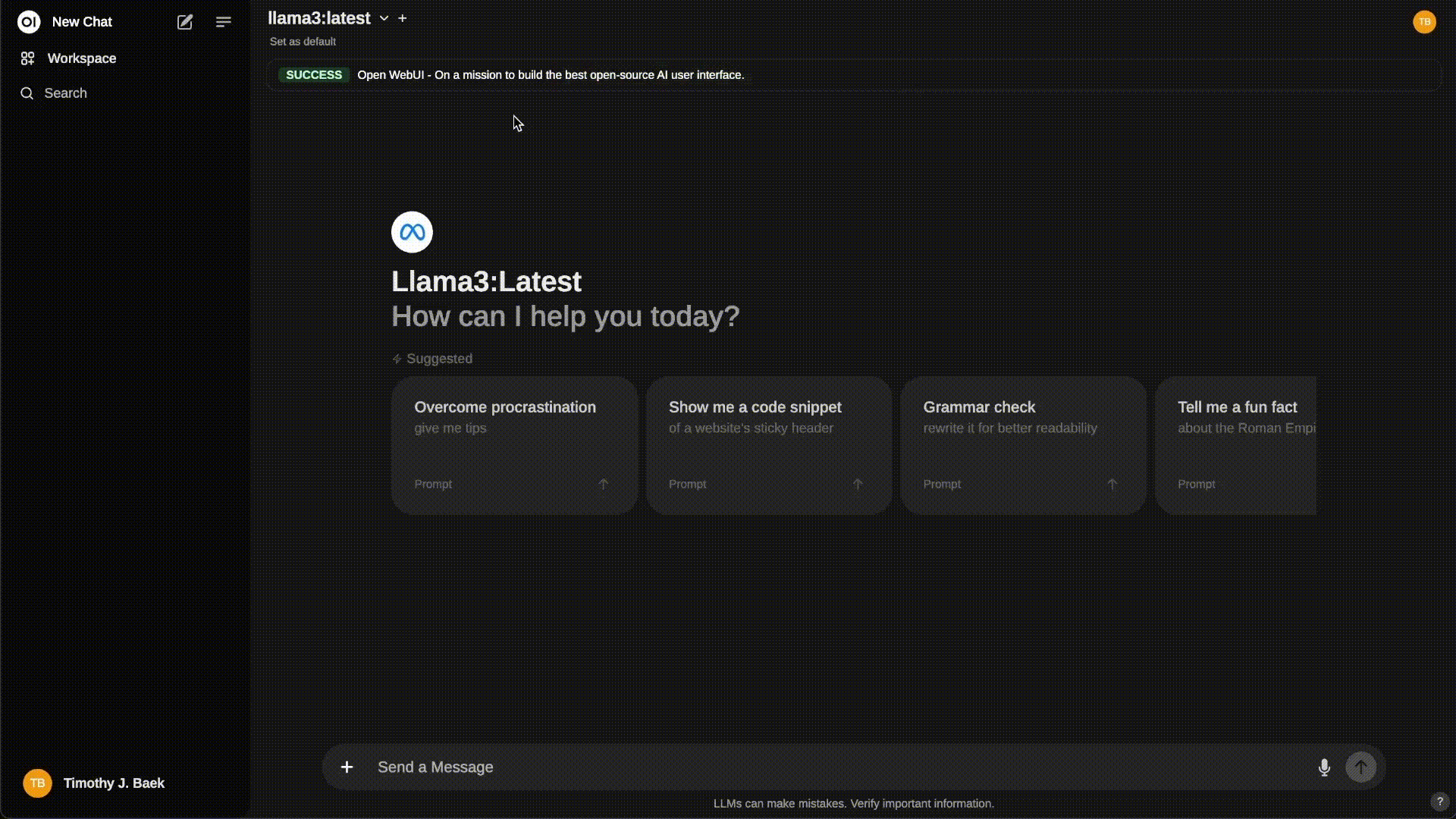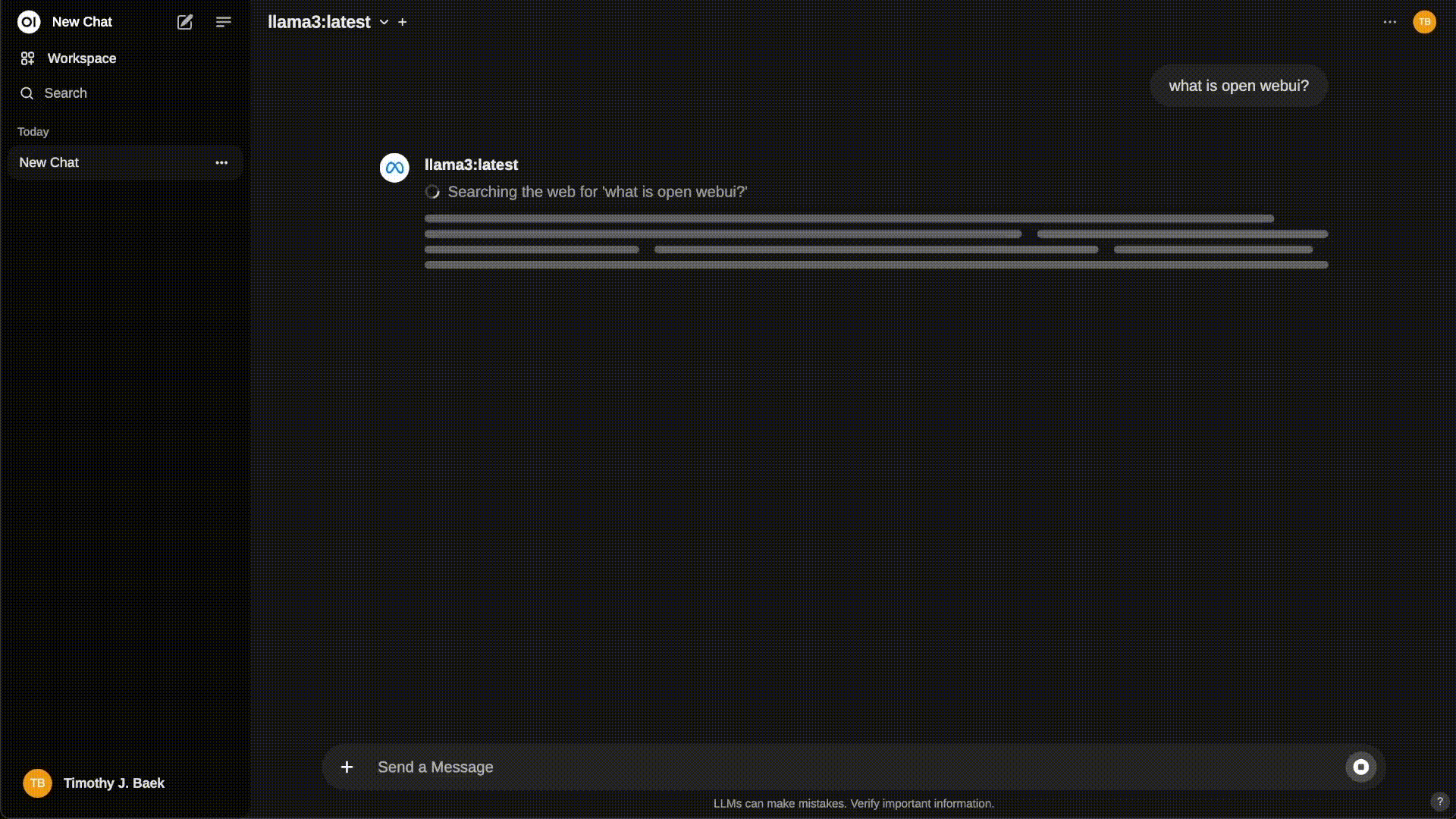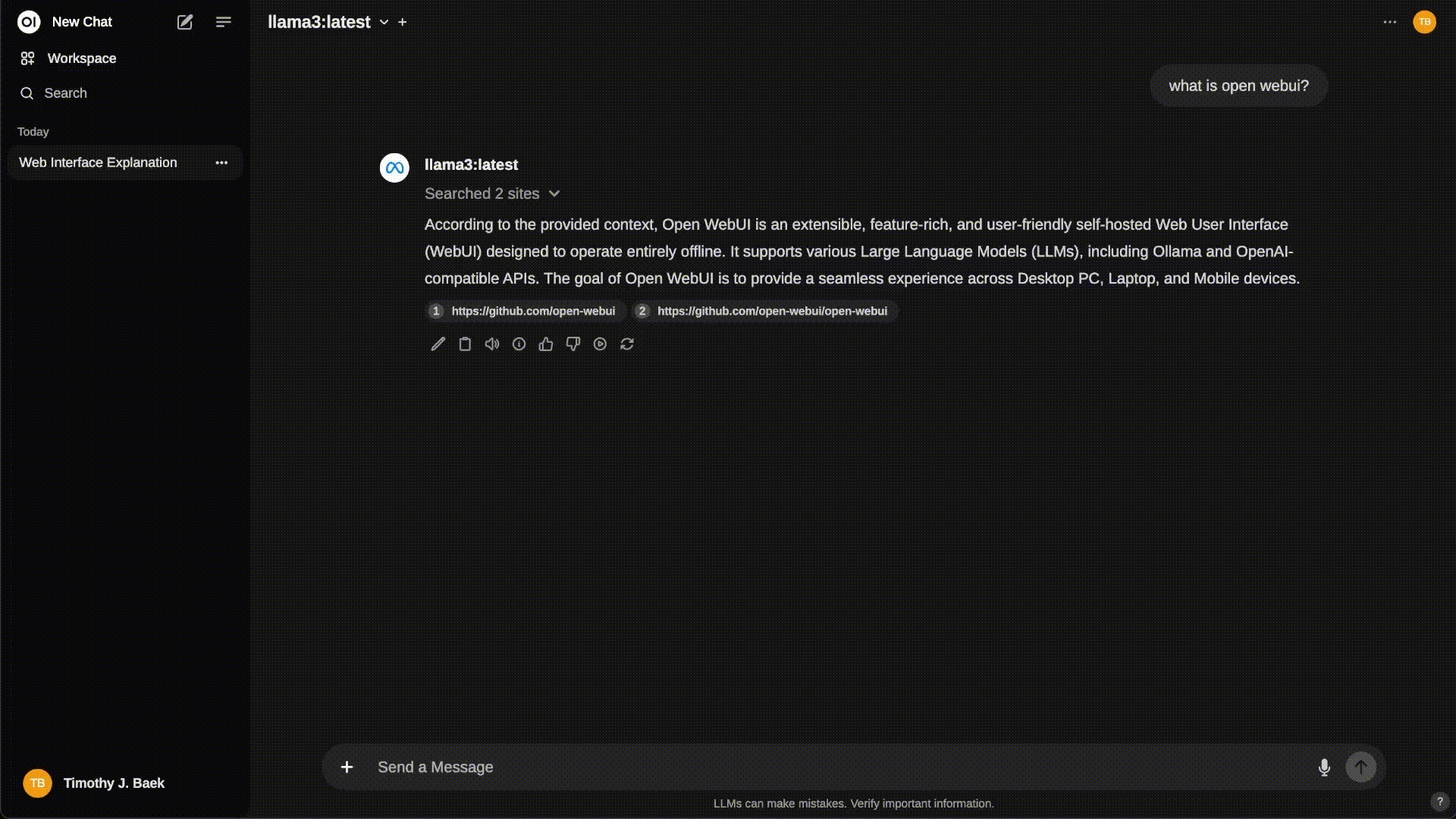
功能介绍
废话不多说,上图!
-
多模型:支持多模型同时对话,比较不同模型的输出结果。

-
图文对话:支持图文对话功能(需模型支持多模态输入),示例:

-
文档 RAG:自带文档 RAG 功能,对所有模型有效:
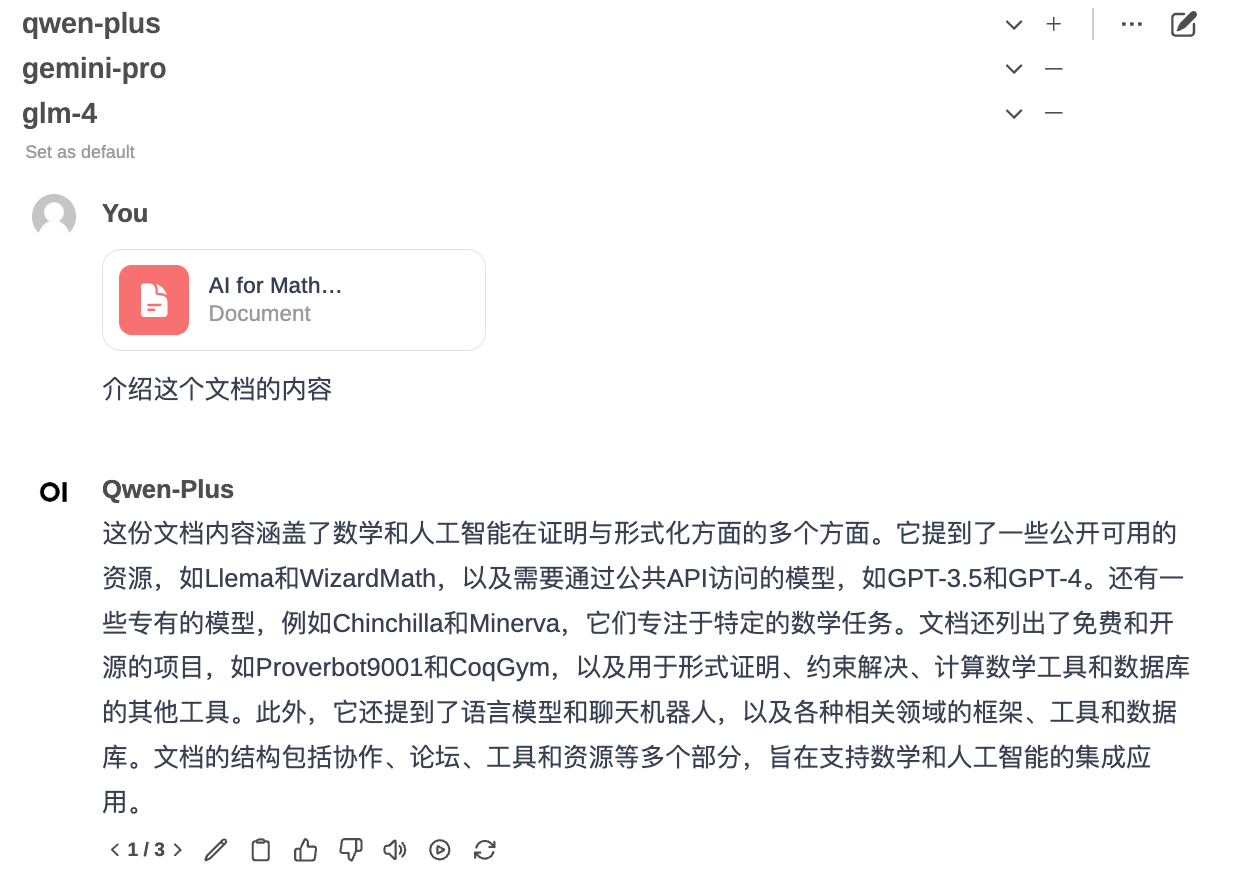
-
语音输入和输出:支持语音输入和输出。
-
网页链接对话:支持使用网页链接对话,通过
#+ 链接,自动下载页面进行 RAG 检索,示例: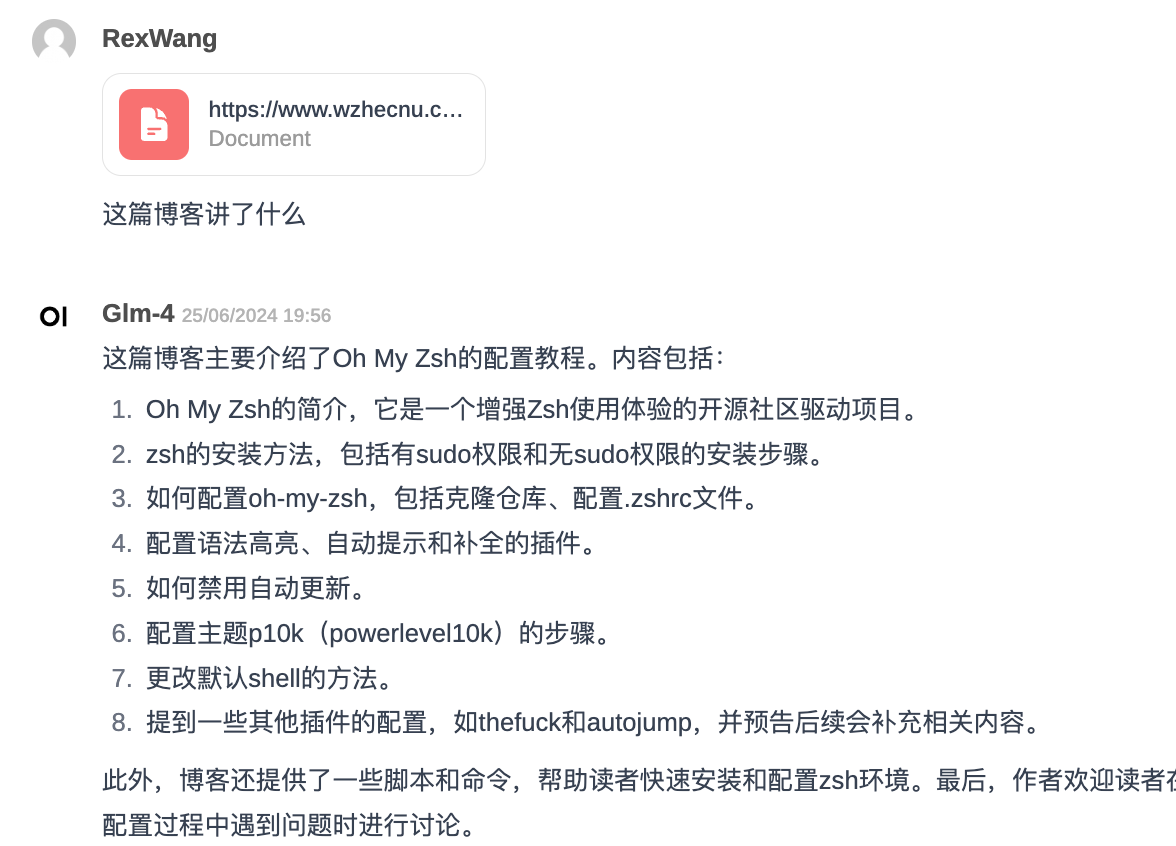
-
端侧运行 Python:使用 WebAssembly 技术,在用户侧运行 Python 代码,示例:
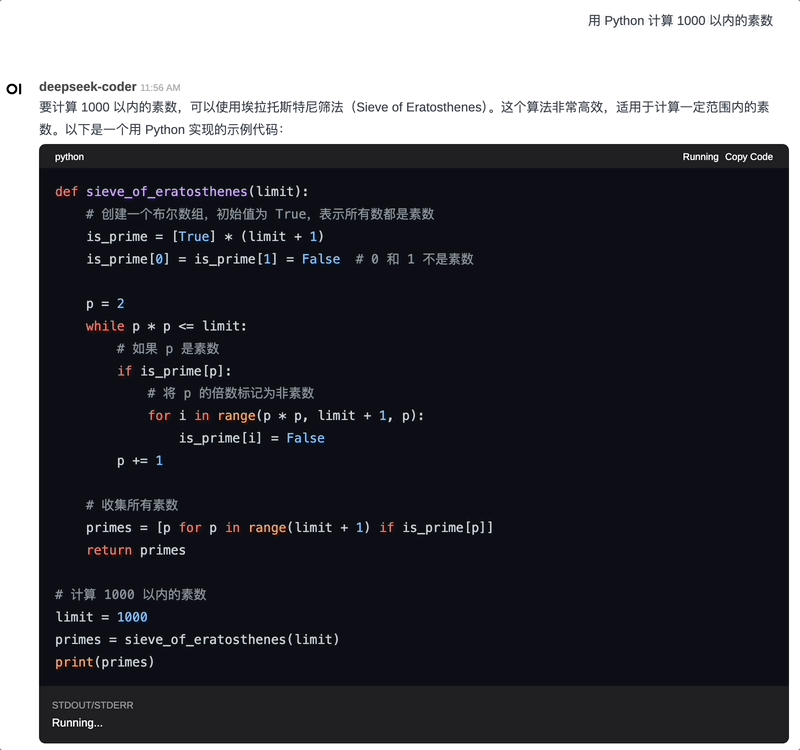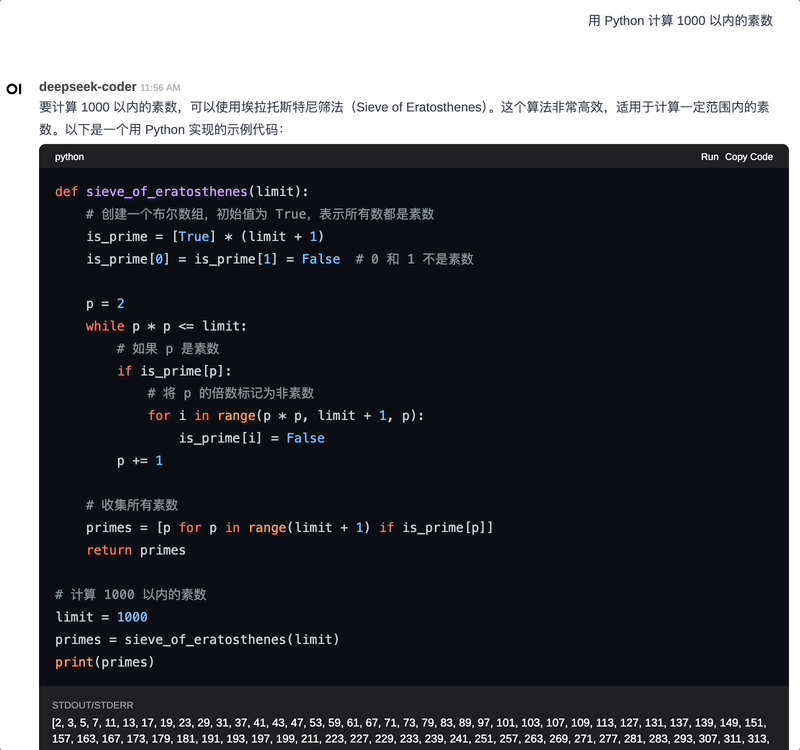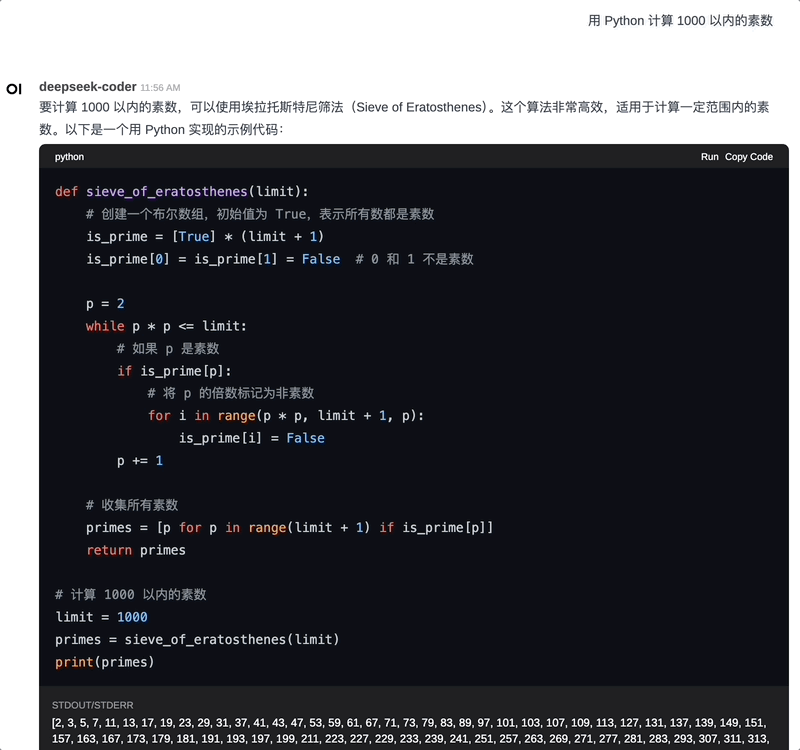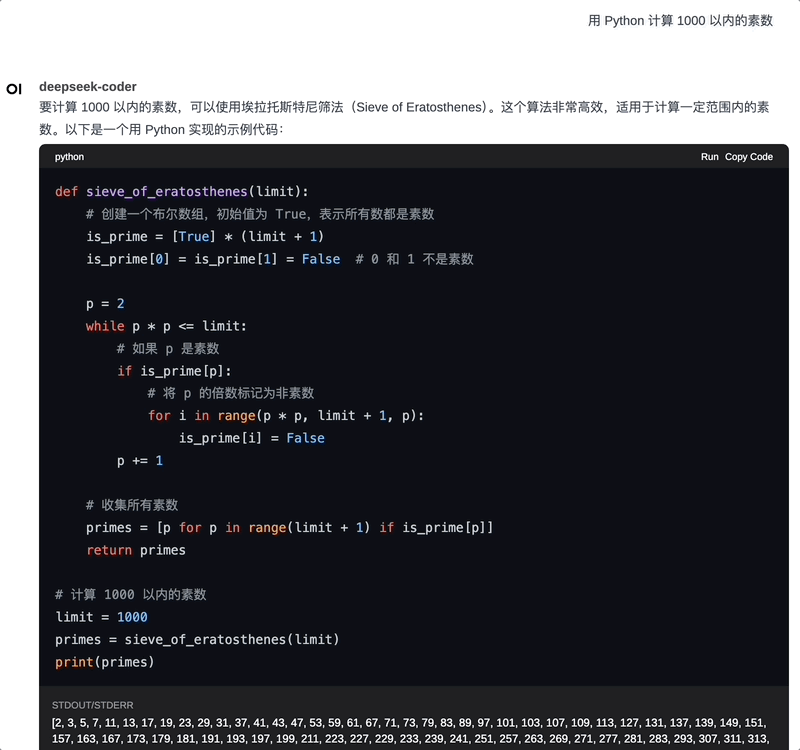
此外,还有很多功能,比如对话分享,工具 Pipeline 等,我们后续介绍。
特别一提这里的端侧技术:
端侧技术能极大降低用户跑代码的门槛,用户不需要配环境,装软件,有浏览器就行,甚至手机浏览器也可以跑代码。端侧技术能给非计算机专业的群体带来有更好的体验,同时不需要网站提供者提供计算资源,避免了安全管理,资源维护,并发处理等问题。不过 Open WebUI 目前仅支持 Python 代码,希望未来能支持更多语言。
一个简单的例子,打开这个网页,就能运行 Jupyter,在任何设备上,且不会占用服务器资源。

后边有机会开坑 WebAssembly 技术的介绍和教程,相关阅读:
- awesome-wasm-langs:WebAssembly 支持的语言列表
- JSage:运行 SageMath 等复杂数学包的方式
安装教程
推荐用 Docker 安装,方便管理和后续升级,OpenWebUI 的文档 也提供了使用 pip 以及源码安装的方法。
安装 docker-compose,比如 Ubuntu 系统:
# 安装 docker
sudo apt install docker -y
# 安装 docker-compose
curl -L https://github.com/docker/compose/releases/download/v2.22.0/docker-compose-$(uname -s)-$(uname -m) -o ./docker-compose
chmod +x ./docker-compose
sudo mv ./docker-compose /usr/bin
然后,在存放服务的位置,编写 docker-compose.yml 文件:
sudo mkdir -p /srv/open-webui
cd /srv/open-webui
sudo vim docker-compose.yml
填入以下内容:
version: '3.8'services:open-webui:image: ghcr.io/open-webui/open-webui:maincontainer_name: open-webuirestart: alwaysports:- "8080:8080"volumes:- ./open-webui:/app/backend/dataenvironment:OPENAI_API_BASE_URLS: ${OPENAI_API_BASE_URLS}OPENAI_API_KEYS: ${OPENAI_API_KEYS}OLLAMA_BASE_URL: ${OLLAMA_BASE_URL}WEBUI_SECRET_KEY: ${WEBUI_SECRET_KEY}HF_ENDPOINT: "https://hf-mirror.com"
服务默认端口为 8080,可以根据需要修改,比如改成 3080:8080。
接下来,在同一目录下,编辑 .env 文件,填入相应的环境变量。例如,用于配置代理 OpenAI 的 API:
# 多个链接用分号 ; 分隔
OPENAI_API_BASE_URLS="..."
OPENAI_API_KEYS="sk-..."
如果服务器配了 Ollama,可以设置 Ollama 的 API:
OLLAMA_BASE_URL="..."
API 的配置和获取可以参考:
- 零资源跑大模型:Hugging Face API + LiteLLM + Flask
- 大模型 API 推理全指南 | OneAPI + Ollama + vLLM + ChatTool
当然,如果仅使用 GPT 模型,可以直接找代理站,花钱省事。
可选且推荐设置的环境变量:
# 访问端口,默认为 8080,与 docker-compose.yml 中的端口对应
PORT=8080
# 允许管理员访问用户聊天记录,默认为 true,建议设置为 false
ENABLE_ADMIN_CHAT_ACCESS=false
# 浏览器标签显示的名称
WEBUI_NAME=
# 启动时的默认模型
DEFAULT_MODEL="..."
# 默认角色,支持 admin/user/pending 三种,对应管理员,普通用户和待审核用户
DEFAULT_USER_ROLE=pending
其中,默认模型和角色在管理员页面可以重新修改。
以上列举了几个常用变量的设置,完整选项可以在这里找到。其中涉及 Pipline 等需进一步配置才能启用的特性,我们在后续更新中介绍。
最后,启动服务:
sudo docker-compose up -d
访问服务后,首次注册的用户会被设置为管理员,管理员可以修改网站设置,以及修改其他用户角色。
另外,所有聊天记录存储在云端。
Nginx 反向代理
设置 Nginx 反向代理,以便通过域名访问,比如 webui.example.com。参考配置如下:
server {listen 443 ssl;server_name webui.example.com;ssl_certificate ...;ssl_certificate_key ...;location / {proxy_pass http://localhost:3080; # 与 docker-compose.yml 中的端口对应}
}server {listen 80;server_name webui.example.com;return 301 https://$host$request_uri;
}
关于 ssl 证书的配置,可以参考之前写的博文 Let‘s Encrypt 域名证书增强网站安全。
高级特性
函数调用,Pipeline 以及文生图等功能,后续再更新介绍~(TODO)
