平台和自建网站服务提供者wordpress用多大主机
关于国产自主代替的问题是当前热点,尤其是工业软件领域。
“一个功能强大的全自主C++跨平台图形可视化架构对开发自主可控工业基础软件至关重要!”
作为全球领先的C++工业基础图形可视化软件提供商,UCanCode软件有自己的思考,我们认为要提升国产自主工业软件开发能力的关键在于是否有一个开放的,功能强大的C++基础可视化图形架构,一个稳健,功能强大的图形可视化基础架构上面可以轻松构建各类工业组态监控、人机界面、CAD以及设计电力,能源,科学计算,电路仿真,电力仿真等基础工业软件。
为此,UCanCode花费了极大的精力将原来基于Windows的C++图形可视化架构Form++整体移植到Qt环境下,为国产自主工业软件开发提供一个稳健,功能强大,完全开放的基础架构。下面是VX++架构功能说明:
1、专业的制图模板:

2、类似于Visio的图元管理,总数超过3000个矢量图元,直接拖放支持:
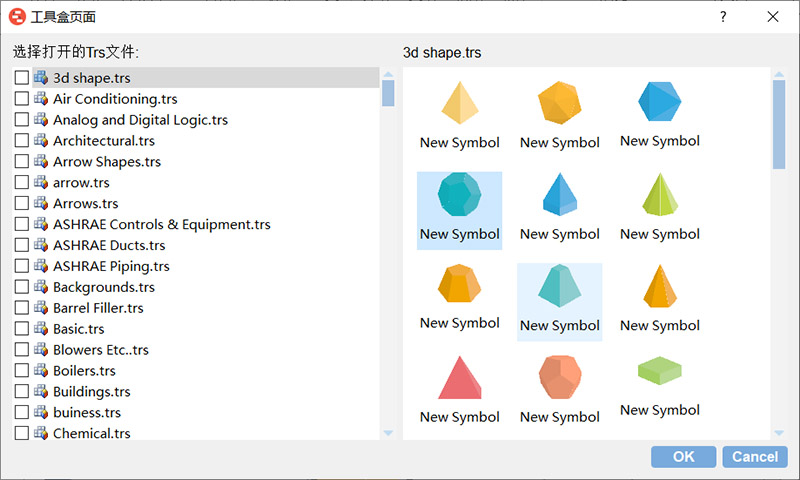
元件可以根据自己的需要任意增加和删除。
3、第三方SVG和CAD图纸导入功能,可以轻松扩展图元:

4、类似于Visio的所有矢量图编辑和排布功能:

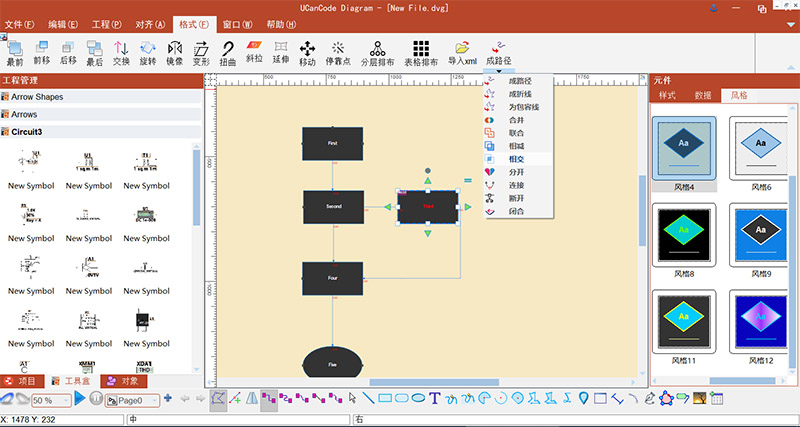
5、元件属性数据自定义:
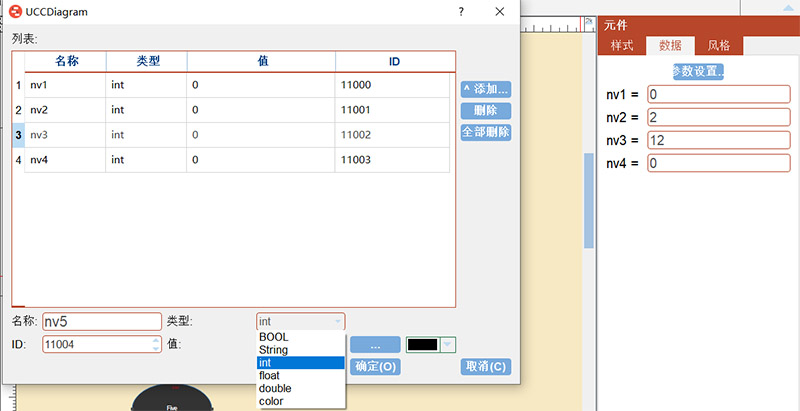
6、脚本自由控制:
每个元件的属性,动画等可以直接使用JavaScript自由控制:

7、图元与图元之间可以多种连接线自由连接:

8、连接线条自动绕开,当线条穿越画布上的图元的时候会自动绕开以避免覆盖,当线条和线条相交的时候会自动建立穿越标记。
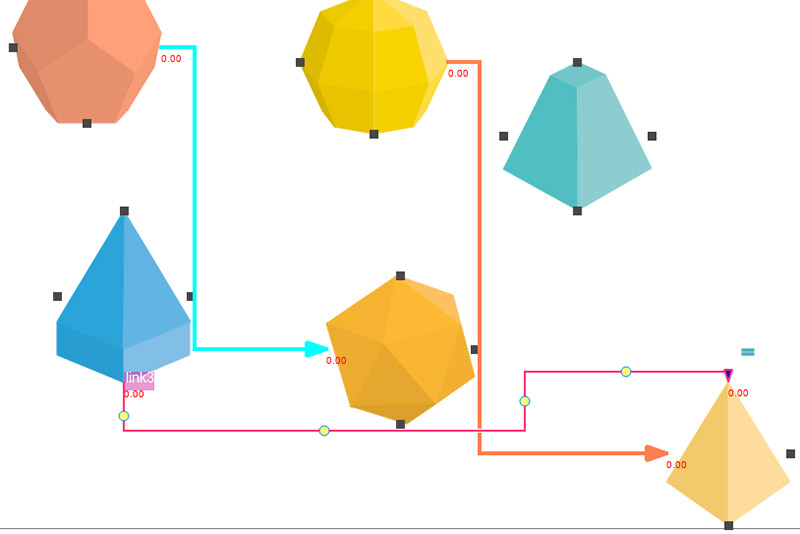
9、自动分层排布,自动分层排布能将复杂的图排布成规则的图:
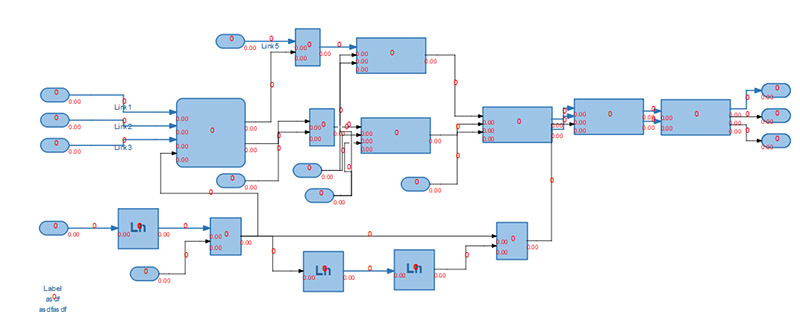
10、多页显示和管理,一个设计文件可以根据需要添加任意多个设计页面。
11、无极缩放和无极Undo/Redo支持。
12、集成IDE支持。可以在一个工程中添加制作多个画面。
13、SVG和Web的导出,支持导出html5+js编程。
14、组态和工业控制元件,包括仪表盘、实时、历史曲线等。
15、提供强大的Chart和表格元件。
16、条码元件支持。
17、自动捕捉、自动对齐功能。
18、高级多边形运算功能,求和、相并、相交、相减、打断、转换曲线等。
19、对多边形镜像、扭曲、变形、拉伸支持。
20、导出为PDF,打印等其他功能...
更加重要的是VX++所有源代码随正式版本100%提供,无任何保留!
VX++的所有核心代码均从UCanCode Form++移植而来,超过20年的客户验证,代码稳健、功能非常强大,是开发任何基础工业软件的必不可少的图形可视化架构。可根据需要扩展为新的工业软件产品。
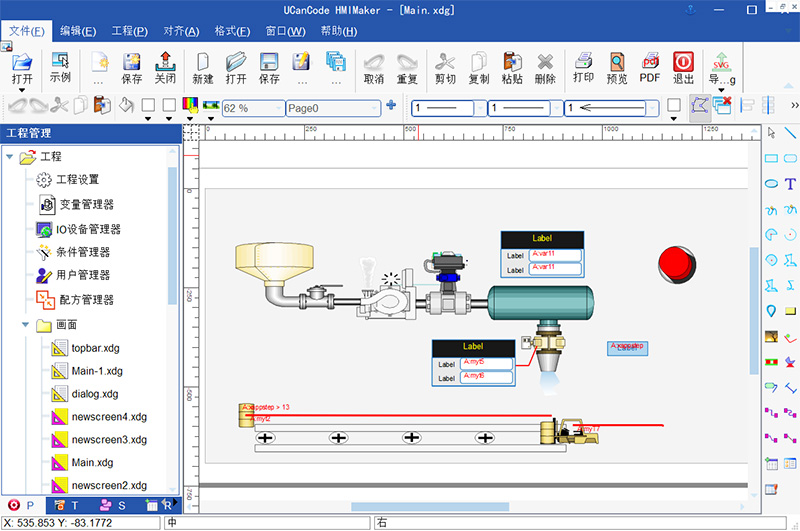
包括各类仿真软件,建模软件,组态软件,工业控制软件,类CAD软件,UML软件等等。
希望能为国产自主可控贡献一些自己的力量!
了解更多,请访问:工控平台仿真平台C++源代码
下载免费试用版本,请访问:下载C++,源代码
