查询网站是否备案上海定制建站网站建设
文章目录
- 一、httpd服务支持的虚拟主机类型包括以下三种:
- 二、构建Web虚拟目录与用户授权限制
- 三、日志分割
虚拟Web主机指的是在同一台服务器中运行多个Web站点,其中每一个站点实际上并不独立占用整个服务器,因此被称为“虚拟”Web 主机。通过虚拟 Web 主机服务可以充分利用服务器的硬件资源,从而大大降低网站构建及运行成本。
使用httpd服务可以非常方便地构建虚拟主机服务器,只需要运行一个httpd服务就能够同时支撑大量的Web站点。Apache虚拟主机相当于一个在同一台服务器中却相互独立的站点,从而实现一台主机对外提供多个 web 服务,每个虚拟主机之间是独立的,互不影响的。
一、httpd服务支持的虚拟主机类型包括以下三种:
1.基于域名:为每个虚拟主机使用不同的域名,但是其对应的 IP 地址是相同的。例如,www.benet.com 和 www.accp.com 站点的 IP 地址都是 192.168.81.129。这是使用最为普遍的虚拟 Web 主机类型。
1)为虚拟主机提供域名解析
通过之前预先编辑好的DNS脚本直接安装完成
2)为虚拟主机准备网页文档
mkdir -p /var/www/html/benet
mkdir -p /var/www/html/accp
echo "<h1>www.benet.com</h1>" > /var/www/html/benet/index.html
echo "<h1>www.accp.com</h1>" > /var/www/html/accp/index.html

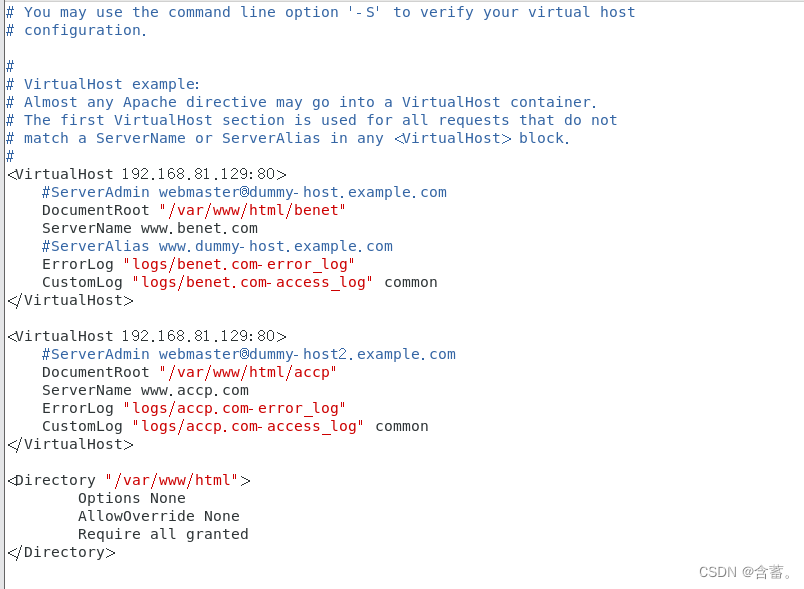
3)添加虚拟主机配置
vim /usr/local/httpd/conf/extra/httpd-vhosts.conf #源码编译安装的虚拟主机配置文件路径
#vim /etc/httpd/conf.d/vhosts.conf #RPM或YUM安装的虚拟主机配置文件路径<VirtualHost 192.168.80.10:80> #设置虚拟主机配置区域
# ServerAdmin webmaster@dummy-host.example.com #设置管理员邮箱,这行可忽略DocumentRoot "/var/www/html/benet" #设置网站根目录ServerName www.benet.com #设置Web站点的完整域名(主机名+域名)
# ServerAlias www.dummy-host.example.comErrorLog "logs/benet.com-error_log" #设置错误日志文件的路径CustomLog "logs/benet.com-access_log" common #设置访问日志文件的路径
</VirtualHost><VirtualHost 192.168.80.10:80> DocumentRoot "/var/www/html/accp" ServerName www.accp.com ErrorLog "logs/accp.com-error_log" CustomLog "logs/accp.com-access_log" common
</VirtualHost>
#设置访问控制
<Directory "/var/www/html"> #设置目录访问权限Options None #不启用任何的服务器特性AllowOverride None #不允许重写Apache默认配置 Require all granted #允许所有主机访问
</Directory>
地址限制策略:
Require all granted:允许所有主机访问。
Require all denied:拒绝所有主机访问。
Require local:仅允许本地主机访问。
Require [not] host <主机名或域名列表>:允许或拒绝指定主机或域名访问。
Require [not] ip <IP 地址或网段列表>:允许或拒绝指定 IP 地址网络访问。
- 加载独立的配置文件,并重启httpd服务
vim /usr/local/httpd/conf/httpd.conf #源码编译安装的httpd服务主配置文件路径
--485行--取消注释systemctl restart httpd
这一步完成后,我再打开一台win10的虚拟机,将ip和dns设置好之后尝试连接

2.基于IP地址:为每个虚拟主机使用不同的域名,且各自对应的IP地址也不相同。这种方式需要为服务器配备多个网络接口,因此应用并不是非常广泛。
1)创建虚拟网卡设置ip需要和源主机在同一网段中
ifconfig ens33:0 192.168.81.150/24
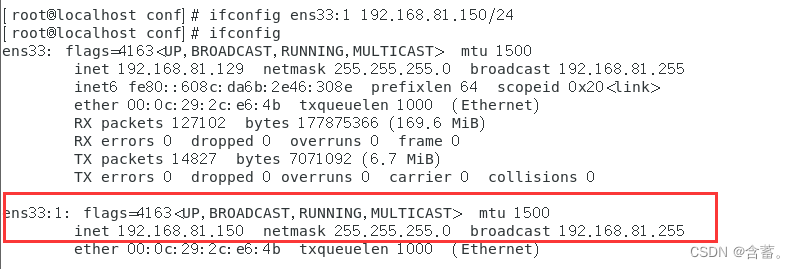
2)添加虚拟主机配置
vim /usr/local/httpd/conf/extra/httpd-vhosts.conf
<VirtualHost 192.168.81.129:80> DocumentRoot "/var/www/html/benet" ServerName www.benet.com ErrorLog "logs/benet.com-error_log" CustomLog "logs/benet.com-access_log" common
</VirtualHost><VirtualHost 192.168.81.150:80> DocumentRoot "/var/www/html/accp" ServerName www.accp.com ErrorLog "logs/accp.com-error_log" CustomLog "logs/accp.com-access_log" common
</VirtualHost><Directory "/var/www/html"> Options None AllowOverride None Require all granted
</Directory>

测试连接状态
3.基于端口:这种方式并不使用域名、IP地址来区分不同的站点内容,而是使用了不同的TCP端口号,因此用户在浏览不同的虚拟站点时需要同时指定端口号才能访问。
添加虚拟主机配置
vim /usr/local/httpd/conf/extra/httpd-vhosts.conf
<VirtualHost 192.168.81.129:80> DocumentRoot "/var/www/html/benet" ServerName www.benet.com ErrorLog "logs/benet.com-error_log" CustomLog "logs/benet.com-access_log" common
</VirtualHost><VirtualHost 192.168.81.129:8080> DocumentRoot "/var/www/html/accp" ServerName www.accp.com ErrorLog "logs/accp.com-error_log" CustomLog "logs/accp.com-access_log" common
</VirtualHost><Directory "/var/www/html"> Options None AllowOverride None Require all granted
</Directory>
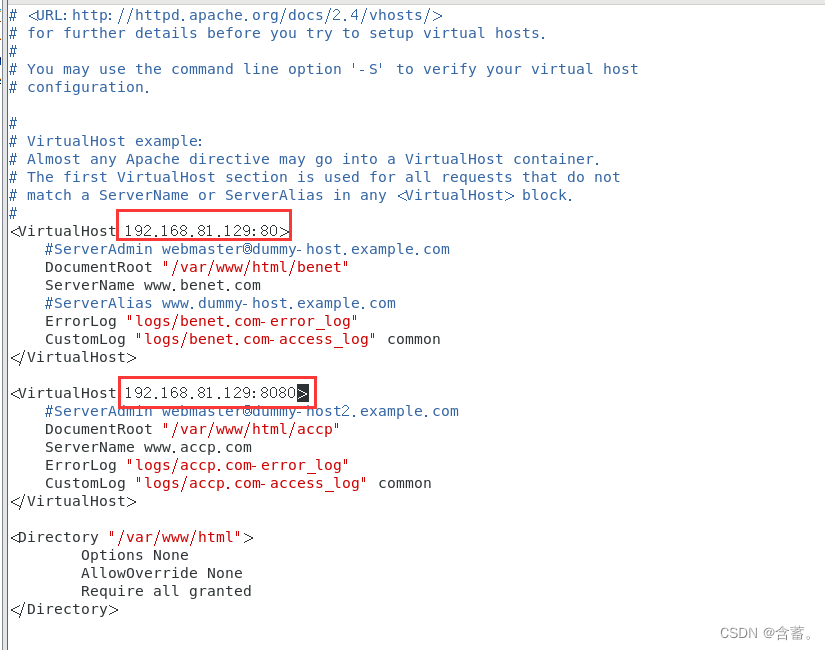
2)修改httpd的配置文件
vim /usr/local/httpd/conf/httpd.conf
--53行--插入
Listen 192.198.81.129:8080
Listen 192.198.81.129:8080systemctl restart httpd

测试连通性
二、构建Web虚拟目录与用户授权限制
修改/usr/local/httpd/conf,vim /httpd.conf,在底行添加配置
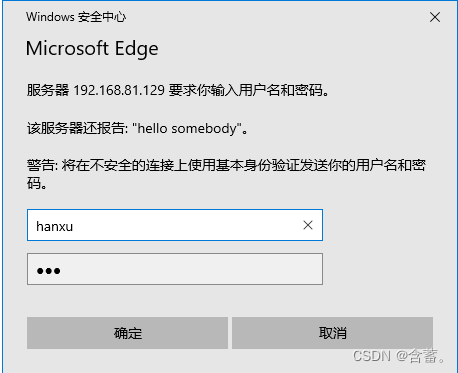
Alias /file /var/www/html/file<Directory "/var/www/html">AllowOverride NoneOptions NoneRequire valid-userAuthName "hello somebody"AuthType BasicAuthUserFile /usr/local/httpd/userlist
</Directory>

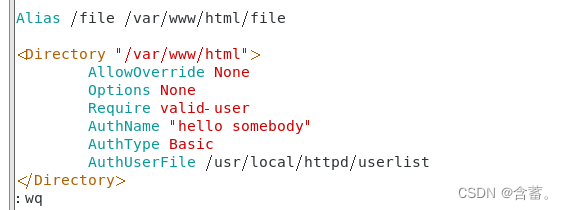
添加用户名和密码
cd /usr/local/httpd/
htpasswd -c /usr/local/httpd/userlist hanxu
htpasswd ./userlist xiaobai

将http的配置文件中的端口号改一下
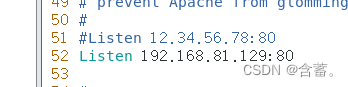
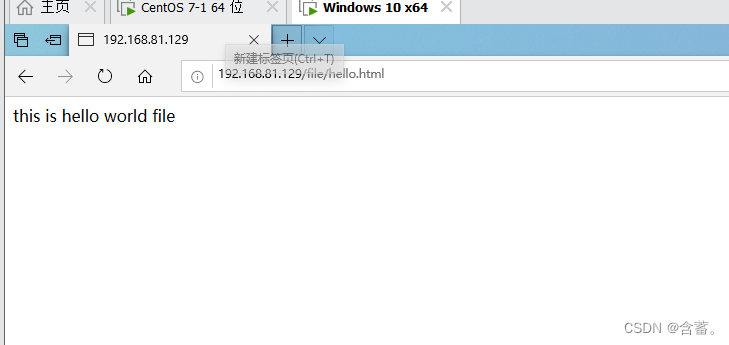
在/var/www/html中添加file文件并写一个hello.html文件。重启httpd服务
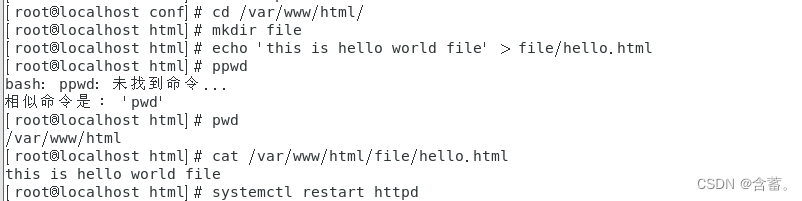
查看连接
如果我输入错误的用户名和密码则会显示错误
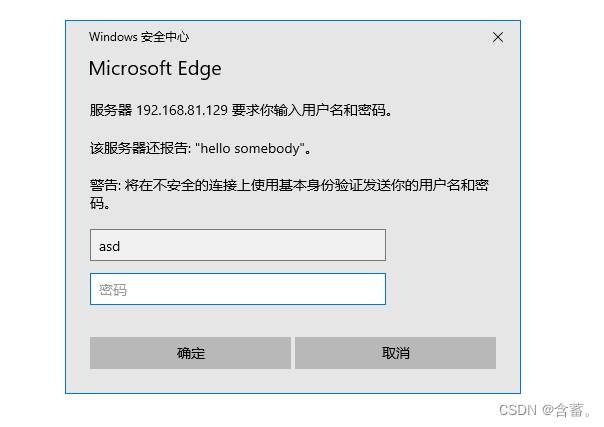
如果输入正确的用户名和密码则登录成功
三、日志分割
使用Apache 自带 rotatelogs 分割工具,将 Apache 的日志进行按每天的日期自动分割。
vim /usr/local/httpd/conf/httpd.conf
--275行--修改
ErrorLog "| /usr/local/bin/rotatelogs -l /var/log/httpd/error_%Y%m%d.log 86400" #分割错误日志
--305行--修改
CustomLog "| /usr/local/bin/rotatelogs -l /var/log/httpd/access_%Y%m%d.log 86400" combined #分割访问日志vim /usr/local/httpd/conf/extra/httpd-vhosts.conf
ErrorLog "| /usr/local/bin/rotatelogs -l /var/log/httpd/benet.com-error_%F.log 86400"
CustomLog "| /usr/local/bin/rotatelogs -l /var/log/httpd/benet.com-access_%F.log 86400" combined#开头的 | 为管道符号。
#-l选项表示使用本地时间为时间基准。
#86400表示一天,即每天生成一个新的日志文件。mkdir /var/log/httpd #创建分割后的日志文件保存目录
systemctl restart httpd浏览器访问
http://192.168.81.129
ls /var/log/httpd



查看一下