一个人能建设一个公司网站吗百度导航是哪个国家的
SSH服务器简介
SSH即Security SHell的意思,它可以将连线的封包进行加密技术,之后进行传输,因此相当的安全。
SSH是一种协议标准,其目的是实现安全远程登录以及其它安全网络服务。
SSH协定,在预设的状态下,本身就提供了两个服务器功能:
一个就是类似telnet的远程连接使用shell的服务器,也就是俗称的SSH。
争另一个就是类似FTP服务的sftp-server,它提供更安全的FTP服务
加密形式:公钥私钥(非对称加密)系统默认就安装了ssh服务端软件 (开源软件openssh-server)
ssh为一种sysV服务,可使用“service”指令来启动
service sshd start
systemctl start sshd
ssh服务器监听的端口为22号端口。(注:ftp是在21,20端口)
SSH安全登录远程主机策略
指定服务器只能由某台主机的某个用户登录:
[root@server39 ~]# vim /etc/ssh/sshd config
将如下两个参数设置为no:
PermitRootLogin no #禁止root用户ssh远程登录
PasswordAuthentication no #禁止用户输入密码(禁止用户用口令登录)
[root@server39~ ]# systemctl restart sshd #重新启动SSH服务
ssh服务器配置文件简介
SSH的配置文件存放在:/etc/ssh/目录中,在此目录中存放了两个基于的配置文件:sshd_config与ssh_ config前一个文件是SSH服务端的配置文件,后一个为SSH客户端的配置。
另外在这个目录中还存放有ssh_host开头的文件,这些文件均为密钥文件。
指纹信息存放在~/ssh/known hosts
运行步骤:

[root@server39 ~]# systemctl start sshd #启动sshd服务
[root@server39 ~]# ssh-keygen #生成SSH密钥对

[root@server39 .ssh]# ssh-copy-id root@192.168.79.132
#是一个用于将本地公钥添加到远程服务器的工具,从而实现无密码登录的命令。
回车后输入“yes”,在输入自己client端的密码

sever端进入client端(要提前把client端打开,才能进入):

在进行两端文件数据互传

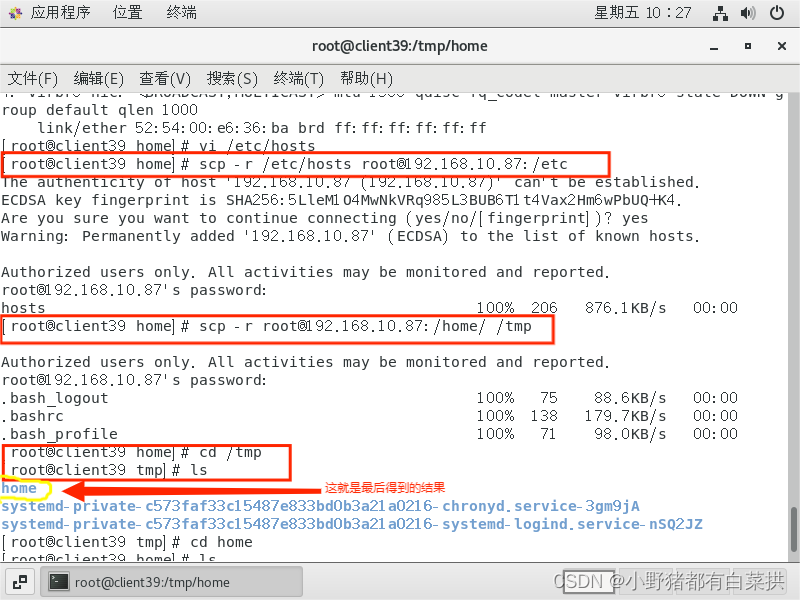
[root@client39 home]#scp -r /etc/hosts root@192.168.10.87:/etc
#本地系统上的/etc/hosts文件复制到远程服务器192.168.10.87的/etc目录下
[root@client39 home]# scp -r root@192.168.10.87:/home/ /tmp
#将远程服务器192.168.10.87上的/home目录及其下的所有内容复制到本地系统的/tmp目录下。
在vi /etc/hosts末尾中写入:
192.168.79.132 server39
192.168.10.87client39
:wq 退出保存
SSH知识点
SSH远程登录服务器命令使用正确的是( ssh user1@192.168.1.10)。
SSH的配置文件存放在( /etc/ssh )目录中,在此目录中存放了两个基于的配置文件,
其中( sshd_config)文件是SSH服务端的配置文件。
客户端创建密钥的命令是命令是( ssh-keygen )。
客户端传输密钥的命令是(ssh-copy-id)。
