找个公司做网站需要注意什么网站搭建心得体会
一、创建对话框基本步骤
- 创建并初始化子窗口部件
- 把子窗口部件放到布局中
- 设置tab键顺序
- 建立信号-槽之间的连接
- 实现对话框中的自定义槽
首先前面三步在这里是通过ui文件里面直接进行的,剩下两步则是通过代码来实现
二、项目创建详细步骤
创建新项目

为项目命名

为类起名并选择基类为QDialog
【如果这里没有选择QDialog而是选择默认的QMainWindow的话会导致后面运行的时候setupUi函数报错】

三、ui可视化对话框界面设计实现详细步骤
双击 gotocelldialog.ui文件打开设计界面,左侧为工具栏,右侧则是进行设计的界面,只需要将左侧的部件拖拽到界面即可实现

先拖拽一个标签、一个行编辑器、一个水平分隔符和两个按钮到界面上

然后修改Lable部件的text为——&Cell Location:
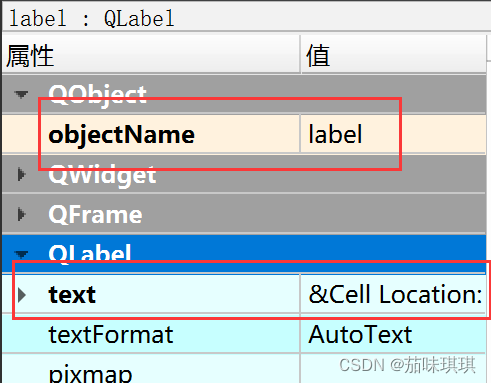
修改第一个按钮的属性,将其text改为——OK,其objectName改为——okButton,其enable属性改为false,其default属性改为——true



修改第二个按钮的属性,将其text改为——Cancel,其objectName改为——cancelButton

修改整个窗体的标题与名字——点击空白部分,然后看属性部分

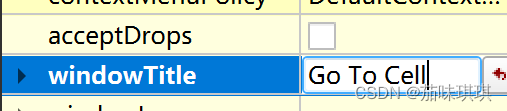
到这里部件属性设置完成
此时界面显示如下:

接下来就是对部件进行绑定还有对布局进行设计
将lable部件与lineEdit部件绑定,点击左上角“编辑”——选择“Edit Buddies”——单击Lable然后将红色箭头与lineEdit连接起来——点击左上角“编辑”——选择“Edit Widget”即可


对布局进行设计
同时选中label还有lineEdit——鼠标右键——布局——水平布局
同时选中下面三个部件——鼠标右键——布局——水平布局
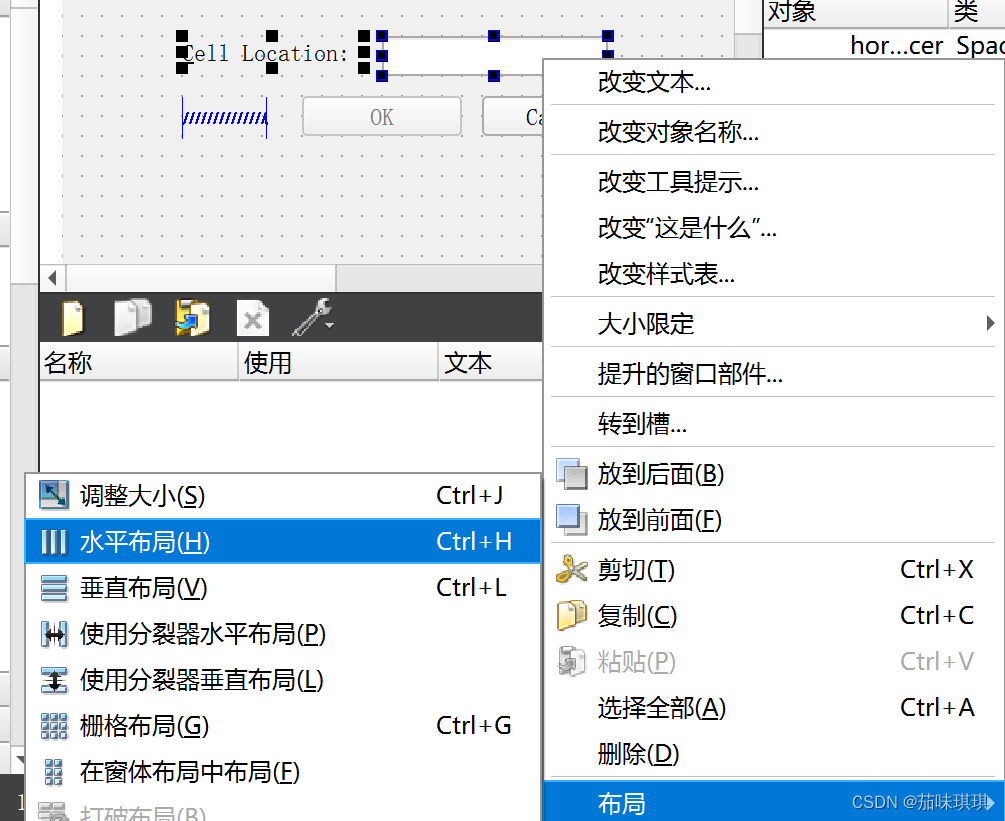

选择窗体中的空白——鼠标右键——布局——调整大小——调整成自己想要的大小——选择窗体中空白——鼠标右键——布局——垂直布局


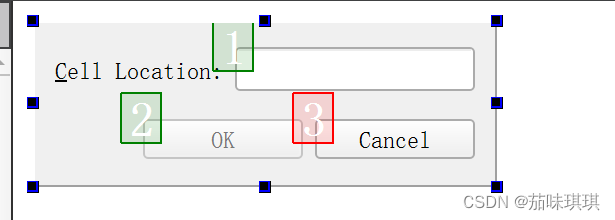
布局设计完成结果如下:

设置Tab键顺序
点击左上角“编辑”——选择“Edit Tab Order”——根据所想顺序进行选择即可

四、对话框实现
①初始实现——使用在ui中设计的窗体、创建QDialog对象、将对象传递给窗体、运行
只需要在main.cpp文件内对代码进行书写
#include "gotocelldialog.h"#include <QApplication>
#include<QDialog>
#include"ui_gotocelldialog.h"int main(int argc, char *argv[])
{QApplication a(argc, argv);//定义窗体、创建QDialog对象、将对象传递给窗体【对话框能展示,但功能没有实现】Ui::GoToCellDialog ui;//定义该窗体QDialog *dialog=new QDialog;//创建一个QDialog对象ui.setupUi(dialog);//把QDialog对象传递给setupUi函数dialog->show()return a.exec();
}
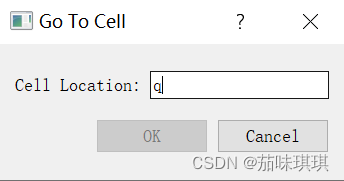
此时会显示前面所设计的界面,但是按钮功能与行编辑器的限制都没有实现

②进阶实现——定义新类继承Ui初始化的GoToCellDialog类还有QDialog并利用信号-槽实现功能
gotocelldialog.h 代码【新类定义】
#ifndef GOTOCELLDIALOG_H
#define GOTOCELLDIALOG_H#include<QDialog>
#include"ui_gotocelldialog.h"//创建一个新类,让此类同时从QDialog和Ui::GoToCellDialog中继承出来,并且实现前面所涉及的窗体中所需要实现的功能
class GoToCellDialog : public QDialog,public Ui::GoToCellDialog
{Q_OBJECTpublic:GoToCellDialog(QWidget *parent = nullptr);//构造函数~GoToCellDialog();//析构函数
private slots:void on_lineEdit_textChange();//实现对OK按钮的启用/禁用
private:Ui::GoToCellDialog *ui;
};
#endif // GOTOCELLDIALOG_H
gotocelldialog.cpp 代码【信号与槽绑定与实现】
#include<QtGui>
#include "gotocelldialog.h"//构造函数的实现
GoToCellDialog::GoToCellDialog(QWidget *parent): QDialog(parent)
{setupUi(this);//初始化窗体//设置一个检验器来限制输入的范围 QRegExpValidator内置检验器后面带一个正则表达式QRegExp regExp("[A-Za-z][1-9][0-9]{0,2}");//正则表达式//允许一个大写/小写字母,后面跟着一个范围为1-9的数字,后面再跟一个0个、1个或者2个0-9的数字lineEdit->setValidator(new QRegExpValidator(regExp,this));//第一个connect已经通过setupUi自动建立了//因为setupUi()函数会自动将那些符合on_objectName_signalName()命名惯例的任意槽与其相应的objectName的signalName()信号连接到一起//connect(lineEdit,SIGNAL(textChange(const QString &)),this,SLOT(on_lineEdit_textChange()));//accept()槽是QDialog的,其可以将对话框返回的结果变量设置为QDialog::Accept(其值等于1)connect(okButton,SIGNAL(clicked()),this,SLOT(accept()));//当点击OK按钮时,触发accept()槽//reject()槽是QDialog的,其可以将对话框的值设置为QDialog::Reject(其值等于0)connect(cancelButton,SIGNAL(clicked()),this,SLOT(reject()));//当点击Cancel按钮时,触发reject()槽//可以利用对话框的结果变量判断用户是否单击了OK按钮
}//实现对OK按钮的启用/禁用
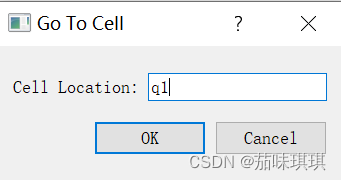
void GoToCellDialog::on_lineEdit_textChange(){//根据行编辑器中是否包含了有效的单元格位置坐标,从而实现对OK按钮的启用或者禁用//hasAcceptableInput()用于判断行编辑器中内容的有效性 有效则禁用,无效则启用okButton->setEnabled(lineEdit->hasAcceptableInput());
}GoToCellDialog::~GoToCellDialog()
{delete ui;
}main.cpp 代码
#include "gotocelldialog.h"#include <QApplication>
#include<QDialog>
#include"ui_gotocelldialog.h"int main(int argc, char *argv[])
{QApplication a(argc, argv);//进阶想法——定义新类继承Ui初始化的类还有QDialog并利用信号-槽实现功能GoToCellDialog *dialog=new GoToCellDialog;dialog->show();return a.exec();
}运行结果:
当行编辑器中的文字不符合输入规定时不允许输入且OK按钮禁用;当行编辑器中内容符合输入规定时OK按钮启用