北方外贸网站建设商务网站规划与建设的目的
本实理论上支持24位图和32位图,实际上只测试了24位。原理很简单,就是RGB中的蓝色字节和红色字节交换。
测试代码1:
#include <stdio.h>
#include <unistd.h>
#include <sys/stat.h>
#include <stdlib.h>
#include <sys/types.h>
#include <fcntl.h>
#include <errno.h>
#include <sys/ioctl.h>
#include <linux/videodev2.h>
#include <sys/mman.h>
#include <string.h>
#include <stdint.h>
#include <jpeglib.h>#define _DEBUG_INFO
#ifdef _DEBUG_INFO
#define DEBUG_INFO(format, ...) printf("%s:%d -- "format"\n" \
,__func__,__LINE__ \
, ##__VA_ARGS__)
#else
#define DEBUG_INFO(format, ...)
#endif//Gray = 0.30 * R + 0.59 * G + 0.11 * B
uint8_t rgb888_to_gray(uint8_t r,uint8_t g,uint8_t b){return (uint8_t)(0.3 *(float)r + 0.59 * (float)g + 0.11 * (float)b);
}typedef uint16_t WORD;
typedef uint32_t DWORD;
#pragma pack(1)
typedef struct tagBITMAPFILEHEADER{WORD bfType;//2DWORD bfSize;//4WORD bfReserved1;//2WORD bfReserved2;//2DWORD bfOffBits;//4
} BITMAPFILEHEADER;
#pragma pack()
typedef int32_t LONG;
#pragma pack(1)
typedef struct tagBITMAPINFOHEADER{DWORD biSize;LONG biWidth;LONG biHeight;WORD biPlanes;WORD biBitCount;DWORD biCompression;DWORD biSizeImage;LONG biXPelsPerMeter;LONG biYPelsPerMeter;DWORD biClrUsed;DWORD biClrImportant;
} BITMAPINFOHEADER; int main(int argc, char **argv)
{char *filename = "RGB.bmp";int fd = open(filename , O_RDONLY);if(fd <= 0){perror("open:");return -1;}struct tagBITMAPFILEHEADER * bit_map_file_header = malloc(sizeof(struct tagBITMAPFILEHEADER));struct tagBITMAPINFOHEADER * bit_map_info_header = malloc(sizeof(struct tagBITMAPINFOHEADER));DEBUG_INFO("%d %d",sizeof(struct tagBITMAPFILEHEADER),sizeof(struct tagBITMAPINFOHEADER));if(bit_map_file_header == NULL || bit_map_info_header == NULL){perror("malloc:");return -1;}//读取bmp的头信息read(fd , bit_map_file_header , 14);if(bit_map_file_header->bfType != 0x4D42){DEBUG_INFO("这不是BMP图片");return -1;}DEBUG_INFO("bfOffBits = %d",bit_map_file_header->bfOffBits);read(fd , bit_map_info_header , 40);DEBUG_INFO("width = %d,height = %d,biBitCount = %d\n" , bit_map_info_header->biWidth , bit_map_info_header->biHeight,bit_map_info_header->biBitCount);if(bit_map_info_header->biBitCount < 24){DEBUG_INFO("仅支持24位和32位的BMP图片");return -1;}if(bit_map_info_header->biWidth < 0){bit_map_info_header->biWidth = abs(bit_map_info_header->biWidth);}if(bit_map_info_header->biHeight < 0){bit_map_info_header->biHeight = abs(bit_map_info_header->biHeight);}DEBUG_INFO("width = %d,%d,biBitCount = %d\n" , bit_map_info_header->biWidth , bit_map_info_header->biHeight,bit_map_info_header->biBitCount);// return 0;int bmp_data_len = bit_map_info_header->biWidth * bit_map_info_header->biHeight * bit_map_info_header->biBitCount;DEBUG_INFO("bmp_data_len = %d",bmp_data_len);unsigned char *bmp_buf = malloc(bmp_data_len);if(bmp_buf == NULL){DEBUG_INFO("malloc error");return -1;}int ret = read(fd,bmp_buf,bmp_data_len);if(ret < 0){DEBUG_INFO("read error");return -1;}//把RGB转换成BGR,就是调用R和G的位置int index = 0;unsigned char tmp;while(bmp_data_len > index){tmp = bmp_buf[index + 0];bmp_buf[index + 0] = bmp_buf[index + 2];bmp_buf[index + 2] = tmp;index += (bit_map_info_header->biBitCount >> 3);}int bgr_bmp_fd = open("BGR.bmp",O_WRONLY | O_TRUNC | O_CREAT,0660);if(fd <= 0){perror("open:");return -1;}write(bgr_bmp_fd,bit_map_file_header,sizeof(struct tagBITMAPFILEHEADER));write(bgr_bmp_fd,bit_map_info_header,sizeof(struct tagBITMAPINFOHEADER));write(bgr_bmp_fd,bmp_buf,bmp_data_len);close(bgr_bmp_fd);close(fd);free(bmp_buf);return 0;
}调试信息:
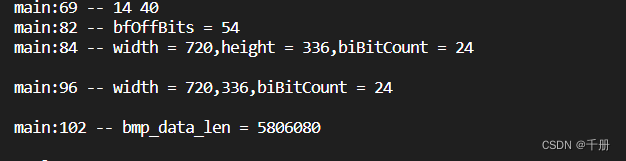
测试结果:
左边是转换之前,右边是转换之后。

由调试信息可知,选取的图片是720X336,也就是行4字节对齐的。换成721X336的图片,测试结果如下:果然出错了。

测试代码2:
修改后的颜色转换部分如下所示:这里主要解决了行4字节对齐的问题。
#include <stdio.h>
#include <unistd.h>
#include <sys/stat.h>
#include <stdlib.h>
#include <sys/types.h>
#include <fcntl.h>
#include <errno.h>
#include <sys/ioctl.h>
#include <linux/videodev2.h>
#include <sys/mman.h>
#include <string.h>
#include <stdint.h>
#include <jpeglib.h>#define _DEBUG_INFO
#ifdef _DEBUG_INFO
#define DEBUG_INFO(format, ...) printf("%s:%d -- "format"\n" \
,__func__,__LINE__ \
, ##__VA_ARGS__)
#else
#define DEBUG_INFO(format, ...)
#endif//Gray = 0.30 * R + 0.59 * G + 0.11 * B
uint8_t rgb888_to_gray(uint8_t r,uint8_t g,uint8_t b){return (uint8_t)(0.3 *(float)r + 0.59 * (float)g + 0.11 * (float)b);
}typedef uint16_t WORD;
typedef uint32_t DWORD;
#pragma pack(1)
typedef struct tagBITMAPFILEHEADER{WORD bfType;//2DWORD bfSize;//4WORD bfReserved1;//2WORD bfReserved2;//2DWORD bfOffBits;//4
} BITMAPFILEHEADER;
#pragma pack()
typedef int32_t LONG;
#pragma pack(1)
typedef struct tagBITMAPINFOHEADER{DWORD biSize;LONG biWidth;LONG biHeight;WORD biPlanes;WORD biBitCount;DWORD biCompression;DWORD biSizeImage;LONG biXPelsPerMeter;LONG biYPelsPerMeter;DWORD biClrUsed;DWORD biClrImportant;
} BITMAPINFOHEADER; char *src_file_name = "RGB2.bmp";
char *dst_file_name = "BGR2.bmp";int main(int argc, char **argv)
{int fd = open(src_file_name , O_RDONLY);if(fd <= 0){perror("open:");return -1;}struct tagBITMAPFILEHEADER * bit_map_file_header = malloc(sizeof(struct tagBITMAPFILEHEADER));struct tagBITMAPINFOHEADER * bit_map_info_header = malloc(sizeof(struct tagBITMAPINFOHEADER));DEBUG_INFO("%d %d",sizeof(struct tagBITMAPFILEHEADER),sizeof(struct tagBITMAPINFOHEADER));if(bit_map_file_header == NULL || bit_map_info_header == NULL){perror("malloc:");return -1;}//读取bmp的头信息read(fd , bit_map_file_header , 14);if(bit_map_file_header->bfType != 0x4D42){DEBUG_INFO("这不是BMP图片");return -1;}DEBUG_INFO("biSizebfOffBits = %d,bfSize = %d",bit_map_file_header->bfOffBits,bit_map_file_header->bfSize);read(fd , bit_map_info_header , 40);DEBUG_INFO("biSize = %d,width = %d,height = %d,biBitCount = %d,biPlanes = %d,\n\biCompression = %d,biSizeImage = %d,\n\biXPelsPerMeter = %d,biYPelsPerMeter = %d,\n\biClrUsed = %d,biClrImportant = %d\n" , bit_map_info_header->biSize,bit_map_info_header->biWidth , bit_map_info_header->biHeight,bit_map_info_header->biBitCount,bit_map_info_header->biPlanes,bit_map_info_header->biCompression,bit_map_info_header->biSizeImage,bit_map_info_header->biXPelsPerMeter,bit_map_info_header->biYPelsPerMeter,bit_map_info_header->biClrUsed,bit_map_info_header->biClrImportant);if(bit_map_info_header->biBitCount < 24){DEBUG_INFO("仅支持24位和32位的BMP图片");return -1;}if(bit_map_info_header->biWidth < 0){bit_map_info_header->biWidth = abs(bit_map_info_header->biWidth);}if(bit_map_info_header->biHeight < 0){bit_map_info_header->biHeight = abs(bit_map_info_header->biHeight);}DEBUG_INFO("width = %d,%d,biBitCount = %d\n" , bit_map_info_header->biWidth , bit_map_info_header->biHeight,bit_map_info_header->biBitCount);// return 0;unsigned char *bmp_buf = malloc(bit_map_file_header->bfSize);unsigned char *dst_bmp_buf = malloc(bit_map_file_header->bfSize);if(bmp_buf == NULL){DEBUG_INFO("malloc error");return -1;}int ret = read(fd,bmp_buf,bit_map_file_header->bfSize - 54);if(ret < 0){DEBUG_INFO("read error");return -1;}int w = bit_map_info_header->biWidth;int h = bit_map_info_header->biHeight;int biBitCount = bit_map_info_header->biBitCount;int color_byte = biBitCount/8;int offset_step;if((w * color_byte)%4){offset_step =((w*color_byte)/4+1)*4;}else{offset_step = w*color_byte;}DEBUG_INFO("offset_step = %d",offset_step);//把RGB转换成BGR,就是调用R和G的位置int index = 0;unsigned char tmp;int offset = 0;DEBUG_INFO("color_byte = %d",color_byte);int line=0;for(int i = 0 ; i < h; i++){for(int j = 0 ; j < w ; j++){int index = offset + j * color_byte;tmp = bmp_buf[index + 0 ];bmp_buf[index + 0 ] = bmp_buf[index + 2 ];bmp_buf[index + 2 ] = tmp; }offset += offset_step;}int bgr_bmp_fd = open(dst_file_name,O_WRONLY | O_TRUNC | O_CREAT,0660);if(fd <= 0){perror("open:");return -1;}write(bgr_bmp_fd,bit_map_file_header,sizeof(struct tagBITMAPFILEHEADER));write(bgr_bmp_fd,bit_map_info_header,sizeof(struct tagBITMAPINFOHEADER));write(bgr_bmp_fd,bmp_buf,bit_map_file_header->bfSize - 54);close(bgr_bmp_fd);close(fd);free(bmp_buf);return 0;
}测试721x336,OK

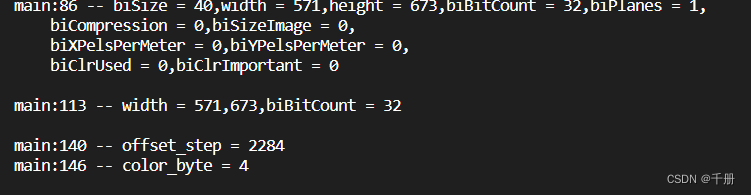
在测一个571X673的,效果还是不错的。

调试信息:宽571,高673,行宽2284字节。