专业 网站设计公司价格自学程序员怎么入门
前言
- 这是一个java的springboot项目,使用maven构建
安装准备
- 需要将maven和jdk安装在服务器上,Jenkins需要用到,还有创建一个jenkins的目录,安装命令如下:
docker run -d -uroot
-p 9095:8080 -p 50000:50000
--name jenkins
-v /data/jenkinsHome:/var/jenkins_home
-v /etc/localtime:/etc/localtime
-v /usr/local/jdk1.8:/usr/local/jdk1.8
-v /usr/local/apache-maven-3.8.5:/usr/local/apache-maven-3.8.5 jenkins/jenkins:2.387.1
开放端口
- 编辑docker.service
vim /usr/lib/systemd/system/docker.service
- 在 ExecStart=/usr/bin/dockerd-current 后 增加
-H tcp://0.0.0.0:2375 -H unix://var/run/docker.sock
私有仓库
docker pull registry
docker run -d -v /var/lib/docker/registry:/var/lib/registry -p 5000:5000 --restart=always registry
- 在/etc/docker/daemon.json中添加一条insecure-registries
{"registry-mirrors": ["xxxxxxxxxxxxxxxxxxxx"], #这是我的加速镜像地址"insecure-registries": ["http://虚拟机ip:5000"]
}
配置Maven和Java
- 在jenkins界面中,进入系统管理-全局工具配置,配置好maven和jdk
- maven:
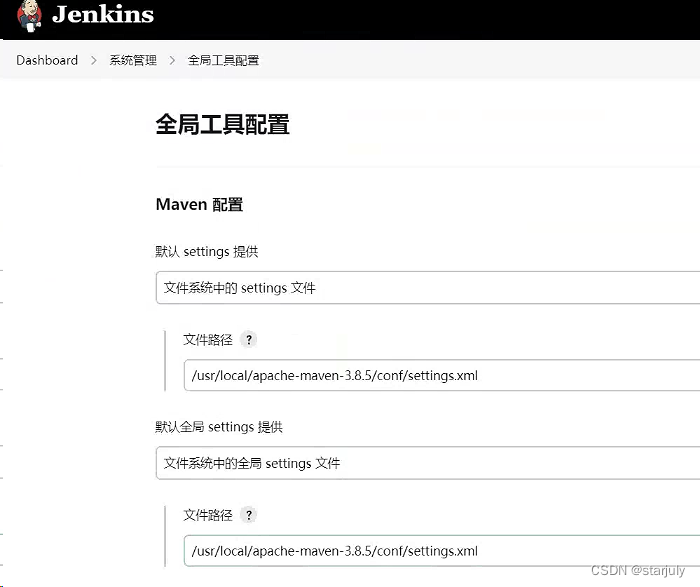
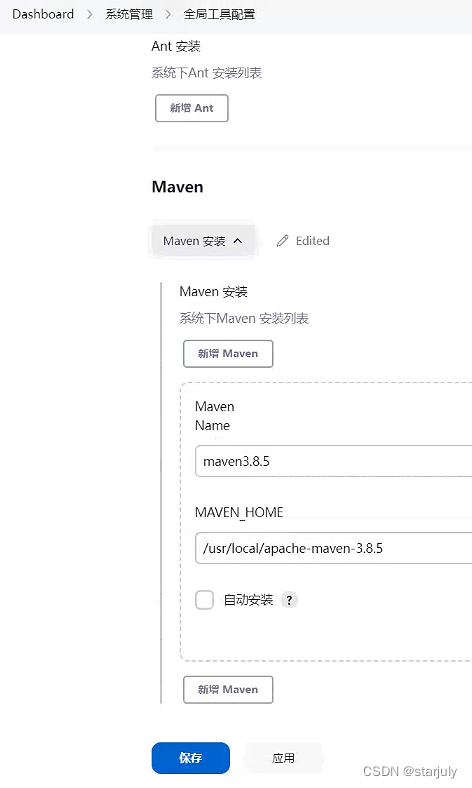
- java: