辽宁省电力建设网站天津市建设协会网站
Webpack 介绍
Date: August 29, 2024
全文概要
Webpack概念:
Webpack是一个静态的模块化的打包工具,可以为现代的 JavaSript 应用程序进行打包。
1-静态:Webpack可以将代码打包成最终的静态资源
2-模块化:webpack支持各种模块化开发,包括ES Module、CommonJS、AMD 等
3-打包:顾名思义,webpack可以帮助我们打包
4-现代:现代前端开发面临各种问题,比如样式兼容性等问题,因而催生了webpack的出现和发展
Webpack最终目的:将各类资源进行打包并生成静态资源。
如何创建局部的webpack:
第一步:创建package.json文件,用于管理项目的信息、库依赖等
npm init -y
第二步:安装局部的webpack
npm install webpack webpack-cli -D
第三步:使用局部的webpack
npx webpack
第四步:在package.json中创建scripts脚本,执行脚本打包即可
npm run build
"scripts": {"build": "webpack"
}
webpack配置文件:
我们通过设立 webpack.config.js 配置来满足一系列要求,配置文件案例如下:
const path = require('path')
// 导出配置信息
module.exports = {entry: './src/main.js',output: {filename: 'bundle.js',path: path.resolve(__dirname, './dist')},module: {rules: [{// 告诉 webpack 匹配什么文件test: /\.css$/,use: ['style-loader', 'css-loader', 'postcss-loader']},{test: /\.less$/,use: ['style-loader', 'css-loader', 'less-loader', 'postcss-loader']}]}
}webpack编写和打包CSS和Less文件
首先,配置对应的 Component 以及 CSS
然后,下载对应的 loader,比如比如 css-loader、less-loader 等
接着,配置 webpack.config.js,以使用以上的各种 loader
最后,采用目录 npm run build 进行打包
拓展,我们可以为以上的各项 loader 进行各种拓展插件配置,比如配置 postcss-loader,我们就可以再专门为其设定一个 postcss.config.js ,并在其中设定对应的 插件,从而更好地处理样式的兼容性问题。
知识准备
前端开发流程
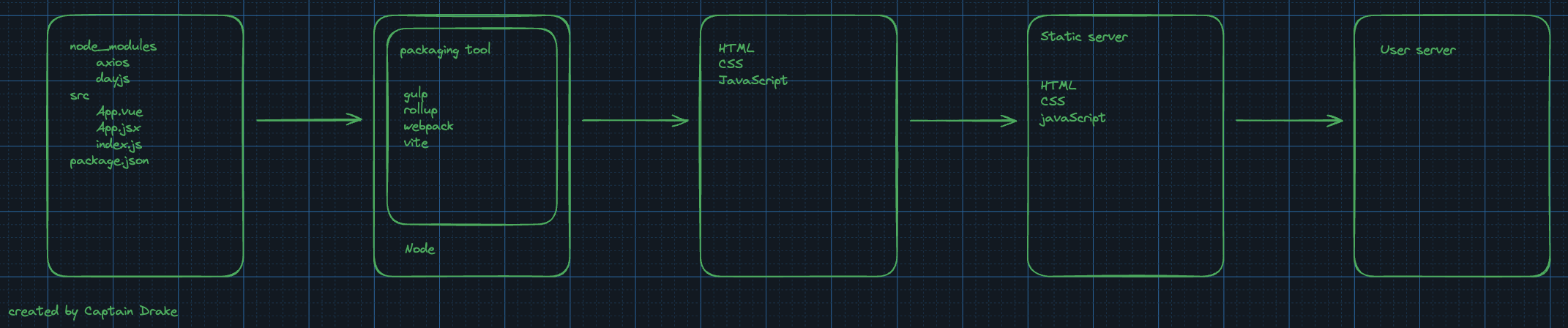
通过Vue、React框架以及npm包管理工具等创建文件,比如 node_modules 模块、App.vue、App.jsx等,这些是浏览器无法识别的。因此,我们需要通过打包工具,比如 Webpack、rollup、Gulp等工具来把以上文件进行转换,生成 Html、CSS、javaScript(ES5)等浏览器能够识别的文件
值得一提的是,以上的一些打包工具,本身也都是js程序,它们的运行环境是 Node。
现在,我们可以通过 Vue CLI、React等脚手架工具来便捷创建文件,但是如果说我们需要对打包的配置做些定制化的配置,就需要手动去配置 Webpack 工具。
path模块
path模块用于对路径和文件进行处理,提供了很多好用的方法。
我们知道在Mac OS、Linux和window上的路径时不一样的
- window上会使用 \或者 \ 来作为文件路径的分隔符,当然目前也支持 /;
- 在Mac OS、Linux的Unix操作系统上使用 / 来作为文件路径的分隔符;
那么如果我们在window上使用 \ 来作为分隔符开发了一个应用程序,要部署到Linux上面应该怎么办呢?
- 显示路径会出现一些问题;
- 所以为了屏蔽他们之间的差异,在开发中对于路径的操作我们可以使用 path 模块;
可移植操作系统接口(英语:Portable Operating System Interface,缩写为POSIX)
Linux和Mac OS都实现了POSIX接口;
Window部分电脑实现了POSIX接口;
PS:这个概念等后期讲 Node 的时候,会涉及到。
path常见的API
从路径中获取信息
dirname:获取文件的父文件夹;
basename:获取文件名;
extname:获取文件扩展名;
路径的拼接:path.join
如果我们希望将多个路径进行拼接,但是不同的操作系统可能使用的是不同的分隔符;
这个时候我们可以使用path.join函数;
案例:将多个路径拼接在一块
我们需要将 path1 和 path2 进行路径拼接:
const path1 = "/abc/cba"
const path2 = "../why/kobe/james.txt"
具体操作:
由于 ../why/kobe/james.txt 指的是上层目录,因此我们理想的最终的拼接结构应该是:
/abc/why/kobe/james.txt
完整操作:
const path = require("path")
const path1 = "/abc/cba"
const path2 = "../why/kobe/james.txt"
console.log(path.join(path1, path2))
拼接绝对路径:path.resolve
- path.resolve() 方法会把一个路径或路径片段的序列解析为一个绝对路径;
- 给定路径的序列是从右往左被处理的,后面每个 path 被依次解析,直到构造完成一个绝对路径
- 如果在处理完所有给定path的段之后,还没有生成绝对路径,则使用当前工作目录;
- 生成的路径被规范化并删除尾部斜杠,零长度path段被忽略;
比如对于 "./abc.txt/" 尾部就多一个/ , path.resolve 就会把这个 / 做一个自动忽略。
比如对于 path.resolve(”./abc/cba”, “”, “../abc.txt”) 中间的””就会被自动忽略。
- 如果没有path传递段,path.resolve()将返回当前工作目录的绝对路径;
比如 console.log(path.resolve("")) 就会直接返回一个绝对路径:
/Users/nathanchen/Downloads/04_Path模块的使用
案例:将多个路径拼接在一块,最终返回一个绝对路径
console.log(path.resolve("./abc/cba", "../why/kobe", "./abc.txt"))
理解:
当 path.resolve 识别到 / 时,会将其识别成一个绝对路径
console.log(path.resolve("./abc/cba", "./a/b", "abc.txt"))
/Users/nathanchen/Downloads/04_Path模块的使用/abc/cba/a/b/abc.txt
当 path.resolve 识别到 ./ 时,会将其识别成一个相对路径,此时就会与前面的路径进行一个拼接。
console.log(path.resolve("./abc/cba", "./a/b", "./abc.txt"))
/Users/nathanchen/Downloads/04_Path模块的使用/abc/cba/a/b/abc.txt
console.log(path.resolve("/a/b", "./abc.txt"))
/a/b/abc.txt
在webpack中的使用
在webpack中获取路径或者起别名的地方也可以使用
webpack: {alias: {"@": resolve("src"),"components": resolve("src/components")}
}
认识 webpack 工具
事实上随着前端的快速发展,目前前端的开发已经变的越来越复杂了:
比如开发过程中我们需要通过模块化的方式来开发;
比如也会使用一些高级的特性来加快我们的开发效率或者安全性,比如通过ES6+、TypeScript开发脚本逻辑,通过sass、less等方式来编写css样式代码;
比如开发过程中,我们还希望实时的监听文件的变化来并且反映到浏览器上,提高开发的效率;
比如开发完成后我们还需要将代码进行压缩、合并以及其他相关的优化;
等等….
但是对于很多的前端开发者来说,并不需要思考这些问题,日常的开发中根本就没有面临这些问题:
这是因为目前前端开发我们通常都会直接使用三大框架来开发:Vue、React、Angular;
但是事实上,这三大框架的创建过程我们都是借助于脚手架(CLI)的;
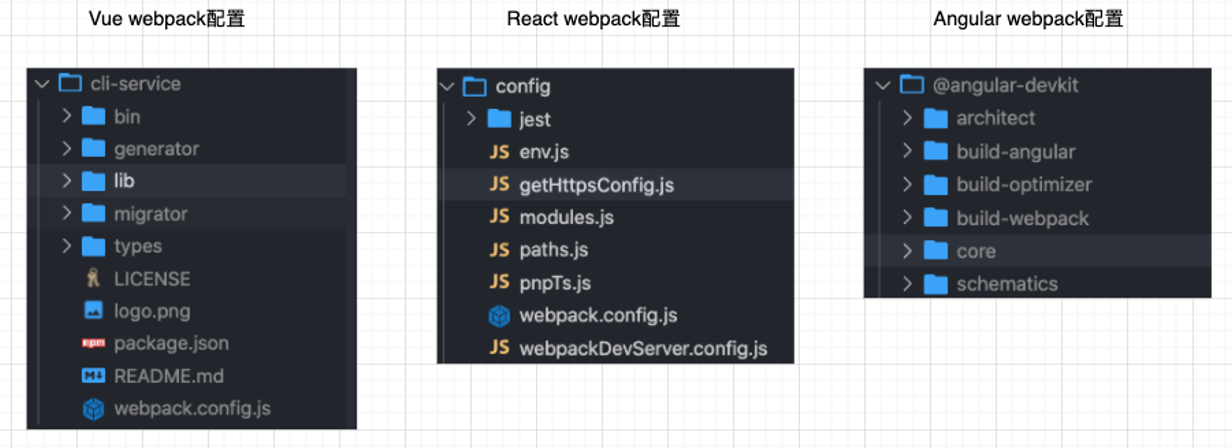
事实上Vue-CLI、create-react-app、Angular-CLI都是基于webpack来帮助我们支持模块化、less、TypeScript、打包优化等的;
事实上我们上面提到的所有脚手架都是依赖于webpack的:
Webpack概念
官方定义:webpack is a static module bundler for modern JavaScript applications.
webpack是一个静态的模块化打包工具,为现代的JavaScript应用程序
我们来对上面的解释进行拆解:
- 打包bundler:webpack可以将帮助我们进行打包,所以它是一个打包工具
- 静态的static:这样表述的原因是我们最终可以将代码打包成最终的静态资源(部署到静态服务器);
- 模块化module:webpack默认支持各种模块化开发,ES Module、CommonJS、AMD等;
- 现代的modern:我们前端说过,正是因为现代前端开发面临各种各样的问题,才催生了webpack的出现和发展;
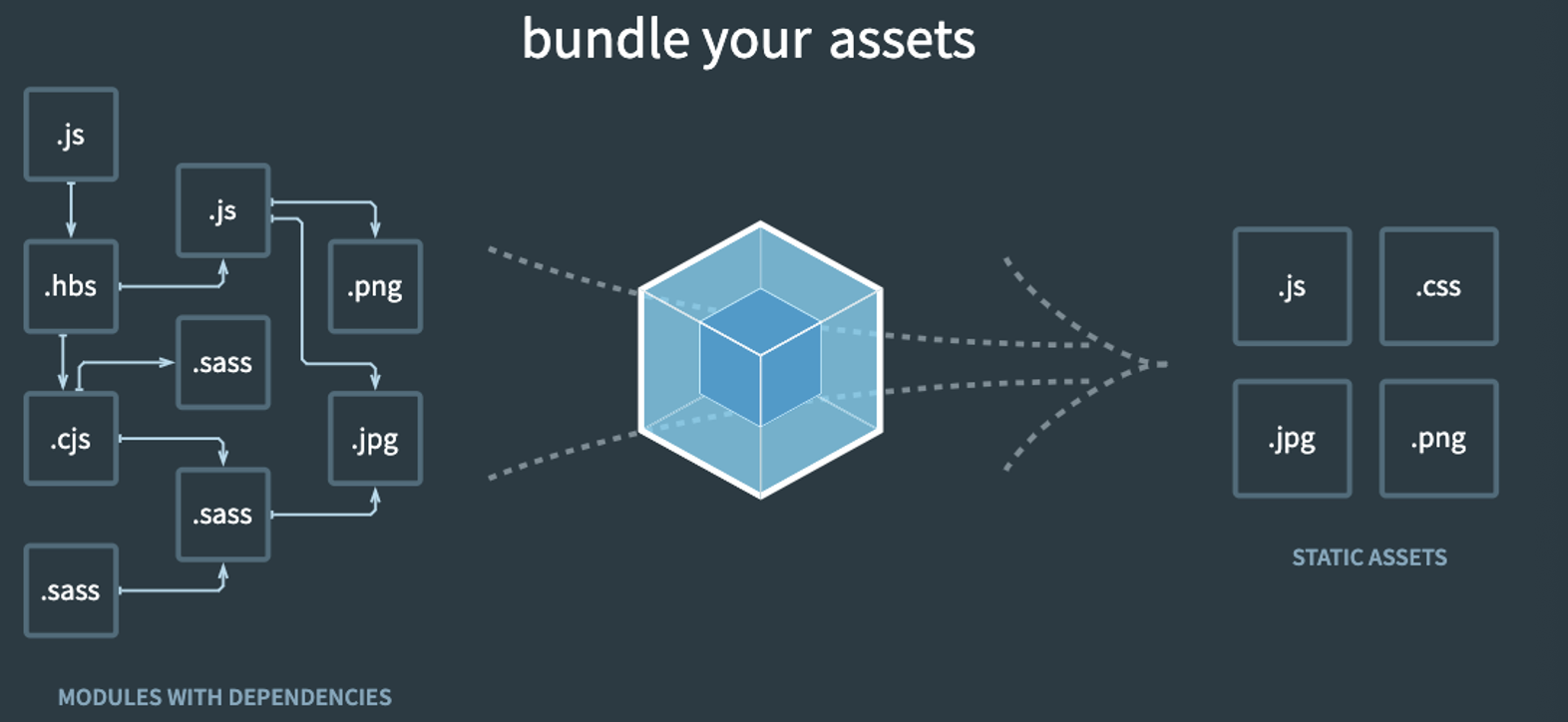
**理解:**各类资源进行打包并生成静态资源。
PS:面试的时候,可以对 Webpack 的定义及其解释做一下阐述即可。
**举例:**Vue项目加载的文件有哪些呢?
- JavaScript的打包:
将ES6转换成ES5的语法;
TypeScript的处理,将其转换成JavaScript;
- Css的处理:
CSS文件模块的加载、提取;
Less、Sass等预处理器的处理;
- 资源文件img、font:
图片img文件的加载;
字体font文件的加载;
- HTML资源的处理:
打包HTML资源文件;
- 处理vue项目的SFC文件.vue文件;
Webpack的使用前提
webpack的官方文档是https://webpack.js.org/
webpack的中文官方文档是https://webpack.docschina.org/
DOCUMENTATION:文档详情,也是我们最关注的
Webpack的运行是依赖Node环境的,所以我们电脑上必须有Node环境
- 需要先安装Node.js,并且同时会安装npm;
- 当前电脑上的node版本是v16.15.1,npm版本是8.11.0(你也可以使用nvm或者n来管理Node版本);
- Node官方网站:https://nodejs.org/
Webpack的安装
webpack的安装目前分为两个:webpack、webpack-cli
那么它们是什么关系呢?
- 执行webpack命令,会执行node_modules下的.bin目录下的webpack;
- webpack在执行时是依赖webpack-cli的,如果没有安装就会报错;
- 而webpack-cli中代码执行时,才是真正利用webpack进行编译和打包的过程;
- 所以在安装webpack时,我们需要同时安装webpack-cli(第三方的脚手架事实上是没有使用webpack-cli的,而是类似于自己的vue-service-cli的东西)

npm install webpack webpack-cli –g # 全局安装
npm install webpack webpack-cli –D # 局部安装
webpack基本打包
Webpack的默认打包
我们可以通过webpack进行打包,之后运行打包之后的代码。
在目录下直接执行 webpack 命令
生成一个dist文件夹,里面存放一个main.js的文件,就是我们打包之后的文件:
- 这个文件中的代码被压缩和丑化了;
- 另外我们发现代码中依然存在ES6的语法,比如箭头函数、const等,这是因为默认情况下webpack并不清楚我们打包后的文件是否需要转成ES5之前的语法,后续我们需要通过babel来进行转换和设置;
我们发现是可以正常进行打包的,但是有一个问题,webpack是如何确定我们的入口的呢?
事实上,当我们运行webpack时,webpack会查找当前目录下的 src/index.js作为入口;
所以,如果当前项目中没有存在src/index.js文件,那么会报错;
当然,我们也可以通过配置来指定入口和出口
npx webpack --entry ./src/main.js --output-path ./build
创建局部的webpack
前面我们直接执行webpack命令使用的是全局的webpack,如果希望使用局部的可以按照下面的步骤来操作。
第一步:创建package.json文件,用于管理项目的信息、库依赖等
npm init -y
第二步:安装局部的webpack
npm install webpack webpack-cli -D
第三步:使用局部的webpack
npx webpack
第四步:在package.json中创建scripts脚本,执行脚本打包即可
npm run build
"scripts": {"build": "webpack"
}
个人补充记录:
设置文件入口为 ./src/main.js ,文件出口为 bundle.js
npx webpack --entry ./src/main.js --output-filename bundle.js
webpack配置文件
在通常情况下,webpack需要打包的项目是非常复杂的,并且我们需要一系列的配置来满足要求,默认配置必然是不可以的。
我们可以在根目录下创建一个webpack.config.js文件,来作为webpack的配置文件:
const path = require('path')
// 导出配置信息
module.exports = {entry: "./src/main.js",output: {filename: "bundle.js",path: path.resolve(__dirname, "./dist")}
}
继续执行 webpack 命令,依然可以正常打包
npm run build
可以参考如下树来配置。
文件树如下所示:
.
├── build
│ └── main.js
├── dist
│ └── bundle.js
├── index.html
├── package-lock.json
├── package.json
├── projectTree.md
├── src
│ ├── main.js
│ └── utils
│ └── foo.js
└── webpack.config.js5 directories, 9 files
指定配置文件
但是如果我们的配置文件并不是webpack.config.js的名字,而是其他的名字呢?
- 比如我们将webpack.config.js修改成了 wk.config.js;
- 这个时候我们可以通过 --config 来指定对应的配置文件;
webpack --config wk.config.js
但是每次这样执行命令来对源码进行编译,会非常繁琐,所以我们可以在package.json中增加一个新的脚本:
{"scripts": {"build": "webpack --config wk.config.js"},"devDependencies": {"webpack": "^5.14.0","webpack-cli": "^4.3.1"}
}
之后我们执行 npm run build 来打包即可。
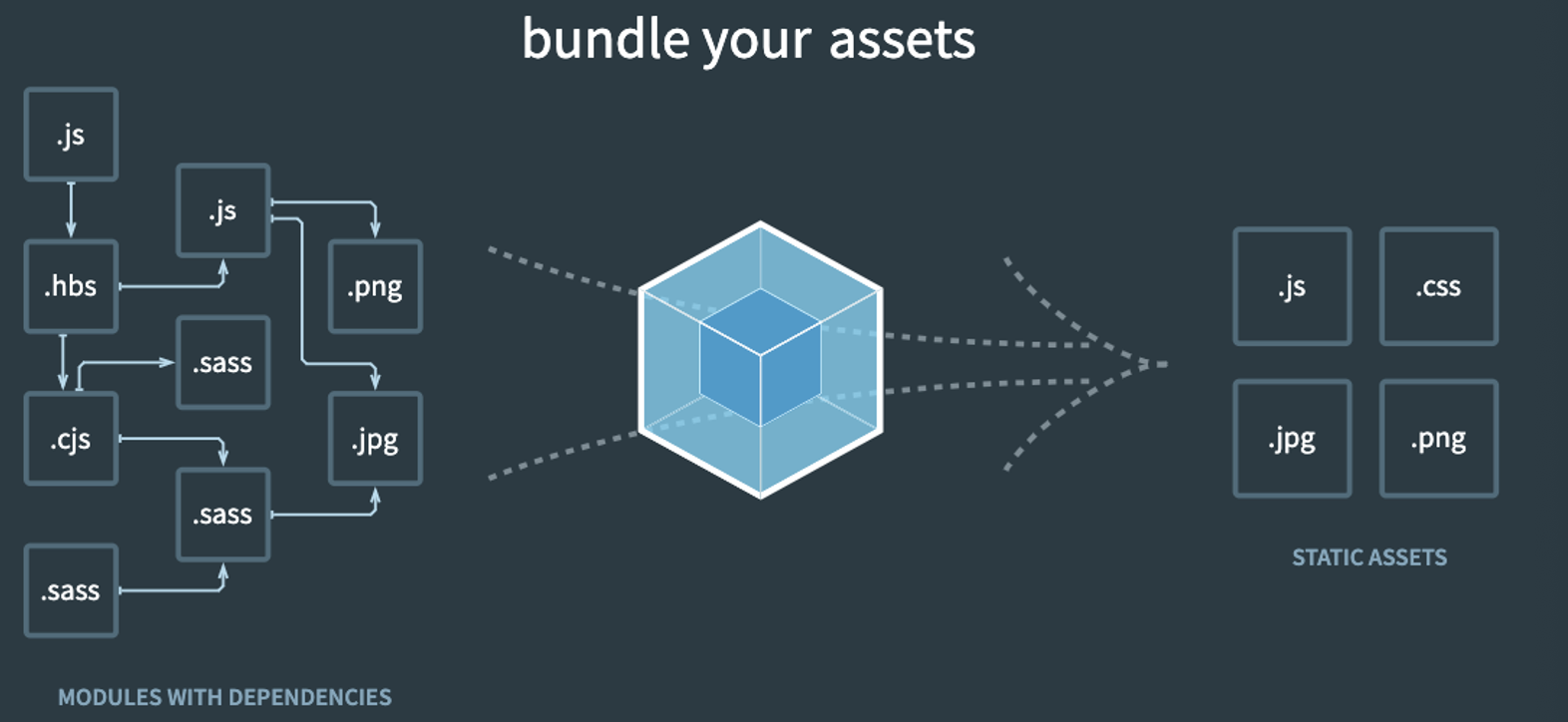
webpack的依赖图
webpack到底是如何对我们的项目进行打包的呢?
事实上webpack在处理应用程序时,它会根据命令或者配置文件找到入口文件;
从入口开始,会生成一个 依赖关系图,这个依赖关系图会包含应用程序中所需的所有模块(比如.js文件、css文件、图片、字体等);
然后遍历图结构,打包一个个模块(根据文件的不同使用不同的loader来解析);
案例
我们创建一个component.js
通过 JavaScript 创建一个元素,并且希望给它设置一些样式;
Case:
位置:src/component/div_cpn.js
import '../css/div_style.css'const divEl = document.createElement('div')divEl.textContent = "Hello World"
divEl.classList.add("content")document.body.append(divEl)
位置:src/css/div_style.css
.content {font-size: 50px;color: red;
}
注意:
1-关于 import '../css/div_style.css'
如果有一份文件仅是通过 import 引入,且没有导出,是可以直接 import 的
当我们接下来对文件的进行打包时,会爆出如下错误:
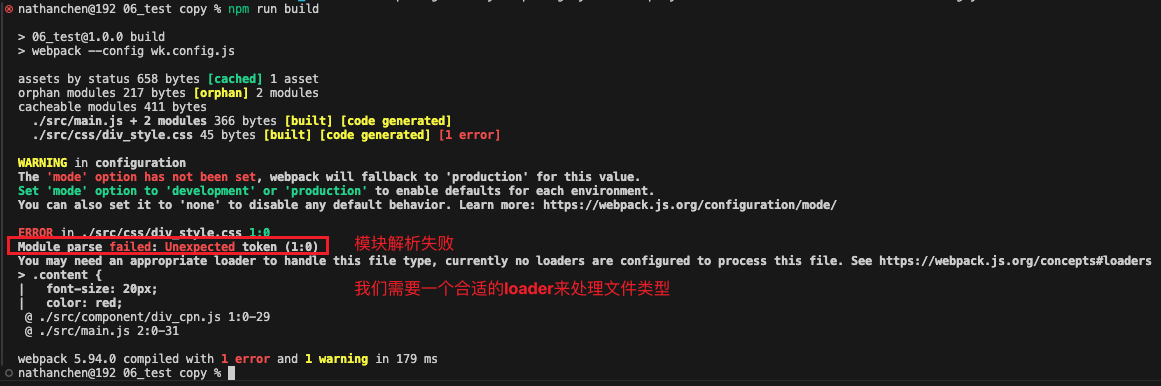
编写和打包CSS文件
css-loader的使用
上面的错误信息告诉我们需要一个loader来加载这个css文件,但是loader是什么呢?
- loader 可以用于对模块的源代码进行转换;
- 我们可以将css文件也看成是一个模块,我们是通过import来加载这个模块的;
- 在加载这个模块时,webpack其实并不知道如何对其进行加载,我们必须制定对应的loader来完成这个功能;
那么我们需要一个什么样的loader呢?
- 对于加载css文件来说,我们需要一个可以读取css文件的loader;
- 这个loader最常用的是css-loader;
css-loader的安装:
npm install css-loader -D
css-loader的使用方案
如何使用这个loader来加载css文件呢?有三种方式:
- 内联方式;
- CLI方式(webpack5中不再使用);
- 配置方式;
**内联方式:**内联方式使用较少,因为不方便管理;
在引入的样式前加上使用的loader,并且使用!分割;
import "css-loader!../css/style.css"
CLI方式
- 在webpack5的文档中已经没有了–module-bind;
- 实际应用中也比较少使用,因为不方便管理;
loader配置方式
配置方式表示的意思是在我们的webpack.config.js文件中写明配置信息:
module.rules中允许我们配置多个loader(因为我们也会继续使用其他的loader,来完成其他文件的加载);
这种方式可以更好的表示loader的配置,也方便后期的维护,同时也让你对各个Loader有一个全局的概览;
module.rules的配置如下:
rules属性对应的值是一个数组:[Rule]
数组中存放的是一个个的Rule,Rule是一个对象,对象中可以设置多个属性:
- test属性:用于对
resource(资源)进行匹配的,通常会设置成正则表达式; - use属性:对应的值时一个数组:[UseEntry]
UseEntry是一个对象,可以通过对象的属性来设置一些其他属性
- loader:必须有一个 loader属性,对应的值是一个字符串;
- options:可选的属性,值是一个字符串或者对象,值会被传入到loader中;
- query:目前已经使用options来替代;
传递字符串(如:use: [ 'style-loader' ])是 loader 属性的简写方式
(如:use: [ { loader: 'style-loader'} ]);
- loader属性: Rule.use: [ { loader } ] 的简写。
Loader的配置代码:
位置:webpack.config.js
const path = require('path')
// 导出配置信息
module.exports = {entry: "./src/main.js",output: {filename: "bundle.js",path: path.resolve(__dirname, "./dist")},module: {rules: [{// 告诉 webpack 匹配什么文件test: /\.css$/,use: [{ loader: "css-loader" }],// 简写一:如果 loader 只有一个// loader: "css-loader"// 简写二:简略 options 写法// use: ["style-loader", "css-loader"]}]}
}
style-loader
我们已经可以通过css-loader来加载css文件了
但是你会发现这个css在我们的代码中并没有生效(页面没有效果)。
原因:
因为css-loader只是负责将.css文件进行解析,并不会将解析之后的css插入到页面中;
如果我们希望再完成插入style的操作,那么我们还需要另外一个loader,就是style-loader;
安装style-loader:
npm install style-loader -D
配置 style-loader
那么我们应该如何使用style-loader:
在配置文件中,添加style-loader;
注意:因为loader的执行顺序是从右向左(或者说从下到上,或者说从后到前的),所以我们需要将style-loader写到css-loader的前面;
use: [// 注意:style-loader在css-loader的前面{ loader: "style-loader" },{ loader: "css-loader" },
]
重新执行编译npm run build,可以发现打包后的css已经生效了:
当前目前我们的css是通过页内样式的方式添加进来的;
后续我们也会讲如何将css抽取到单独的文件中,并且进行压缩等操作;
编写和打包LESS文件
在我们开发中,我们可能会使用less、sass、stylus的预处理器来编写css样式,效率会更高。
那么,如何可以让我们的环境支持这些预处理器呢?
首先我们需要确定,less、sass等编写的css需要通过工具转换成普通的css;
比如我们编写如下的less样式:
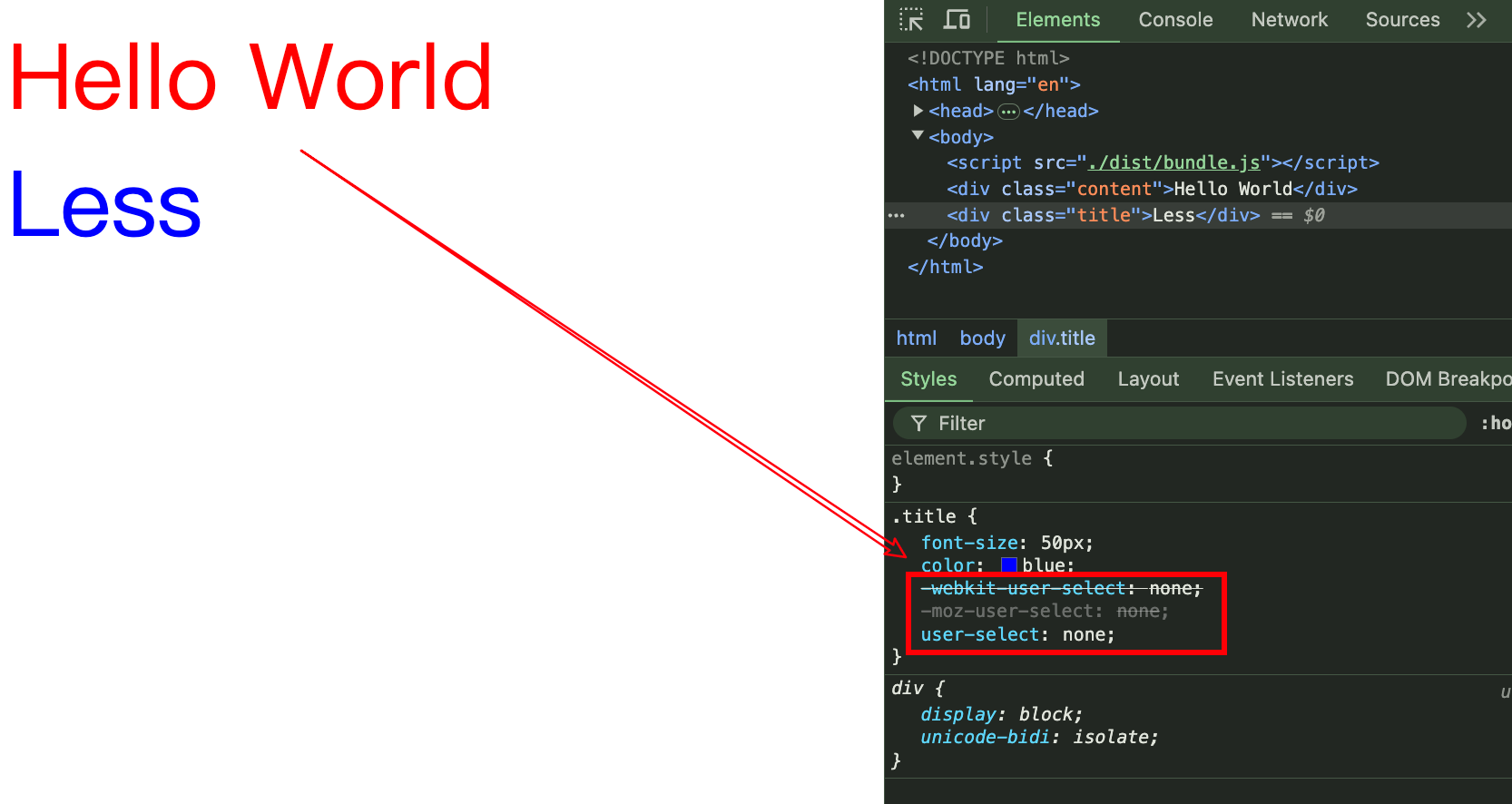
@fontSize: 50px;
@fontColor: blue;.title {font-size: @fontSize;color: @fontColor;user-select: none;
}
Less工具处理
我们可以使用 less 工具来完成它的编译转换:
npm install less -D
执行如下命令:
npx lessc ./src/css/title.less title.css
less-loader处理
但是在项目中我们会编写大量的css,它们如何可以自动转换呢?
这个时候我们就可以使用less-loader,来自动使用less工具转换less到css;
npm install less-loader -D
配置webpack.config.js
const path = require('path')
// 导出配置信息
module.exports = {entry: "./src/main.js",output: {filename: "bundle.js",path: path.resolve(__dirname, "./dist")},module: {rules: [{// 告诉 webpack 匹配什么文件test: /\.css$/,use: [{ loader: "style-loader" },{ loader: "css-loader" }],},{test: /\.less$/,use: [{ loader: "style-loader" },{ loader: "css-loader" },{ loader: "less-loader" }]}]}
}
执行 npm run build ,less就可以自动转换成 css,并且页面也会生效了。
postcss工具处理CSS
前言:
我们这里可以直接采用 postcss-preset-env 来处理样式兼容性问题
认识 PostCSS 工具
什么是PostCSS呢?
PostCSS是一个通过JavaScript来转换样式的工具,它可以帮助我们进行一些CSS的转换和适配,比如自动添加浏览器前缀、css样式的重置。
但是实现这些功能,我们需要借助于PostCSS对应的插件;
如何使用PostCSS呢?主要就是两个步骤:
第一步:查找PostCSS在构建工具中的扩展,比如webpack中的postcss-loader;
第二步:选择可以添加你需要的PostCSS相关的插件;
postcss-loader
我们可以借助于构建工具:
在webpack中使用postcss就是使用postcss-loader来处理的;
我们来安装postcss-loader:
npm install postcss-loader -D
我们修改加载css的loader:(配置文件已经过多,给出一部分了)
注意:因为postcss需要有对应的插件才会起效果,所以我们需要配置它的plugin;
{loader: "postcss-loader",options: {postcssOptions: {plugins: [require('autoprefixer')]}}
}
单独的postcss配置文件
因为我们需要添加前缀,所以要安装 autoprefixer :
npm install autoprefixer -D
我们可以将这些配置信息放到一个单独的文件中进行管理:
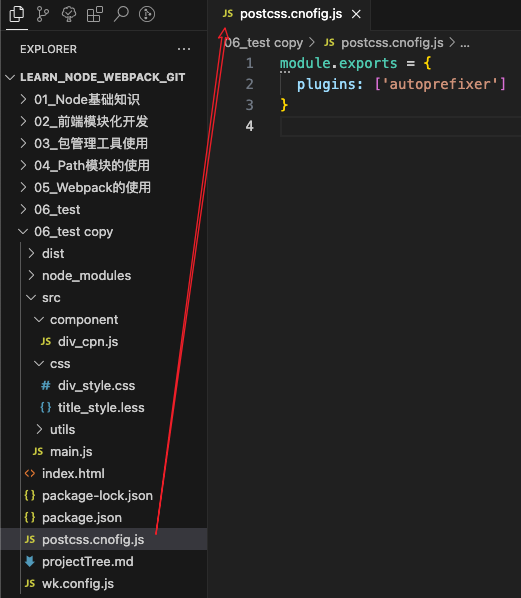
在根目录下创建postcss.config.js
module.exports = {plugins: [require("autoprefixer")]
}
postcss-preset-env
事实上,在配置postcss-loader时,我们配置插件并不需要使用autoprefixer。
我们可以使用另外一个插件:postcss-preset-env
- postcss-preset-env也是一个postcss的插件;
- 它可以帮助我们将一些现代的CSS特性,转成大多数浏览器认识的CSS,并且会根据目标浏览器或者运行时环境添加所需的polyfill;
- 也包括会自动帮助我们添加autoprefixer(所以相当于已经内置了autoprefixer);
首先,我们需要安装postcss-preset-env:
npm install postcss-preset-env -D
顺便要记得配置一下 webpack.config.js
const path = require('path')
// 导出配置信息
module.exports = {entry: "./src/main.js",output: {filename: "bundle.js",path: path.resolve(__dirname, "./dist")},module: {rules: [{test: /\.css$/,use: [ "style-loader", "css-loader", "postcss-loader"]},{test: /\.less$/,use: [ "style-loader", "css-loader", "less-loader", "postcss-loader"]}]}
}
之后,我们直接修改掉之前的autoprefixer即可:
plugins: [require("postcss-preset-env"),
]
注意:我们在使用某些postcss插件时,也可以直接传入字符串
module.exports = {plugins: ["postcss-preset-env",]
}
最终效果: