好的网站你知道张家港做网站排名
1、安装ntp服务后,启动ntpd正常,但是在查看ntpd服务状态时,有一个红色的报错,报错信息如下:
inappropriate address 127.0.0.1 for the fudge command, line ignored
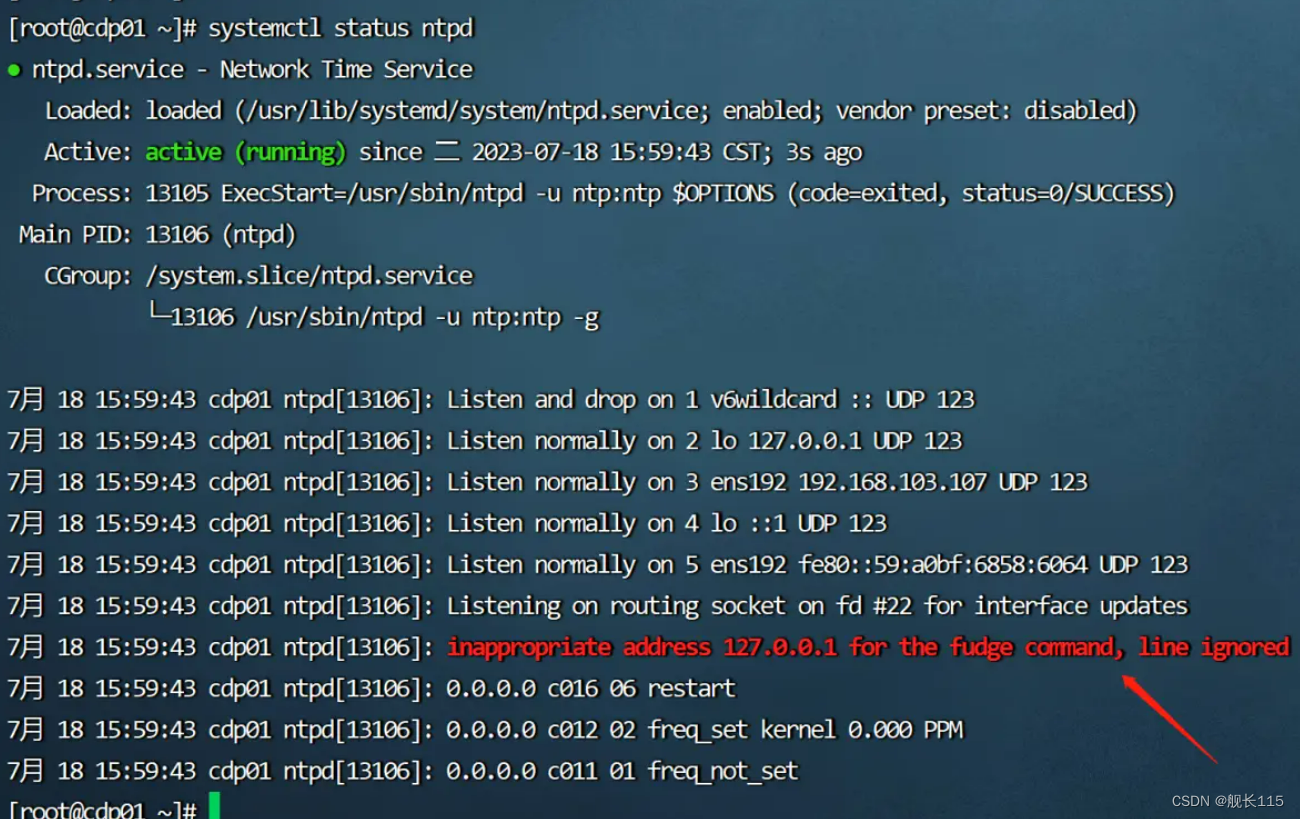
2、解决方法:编辑ntp配置文件:vim /etc/ntp.conf
将fudge修改为:Fudge 注意F大写

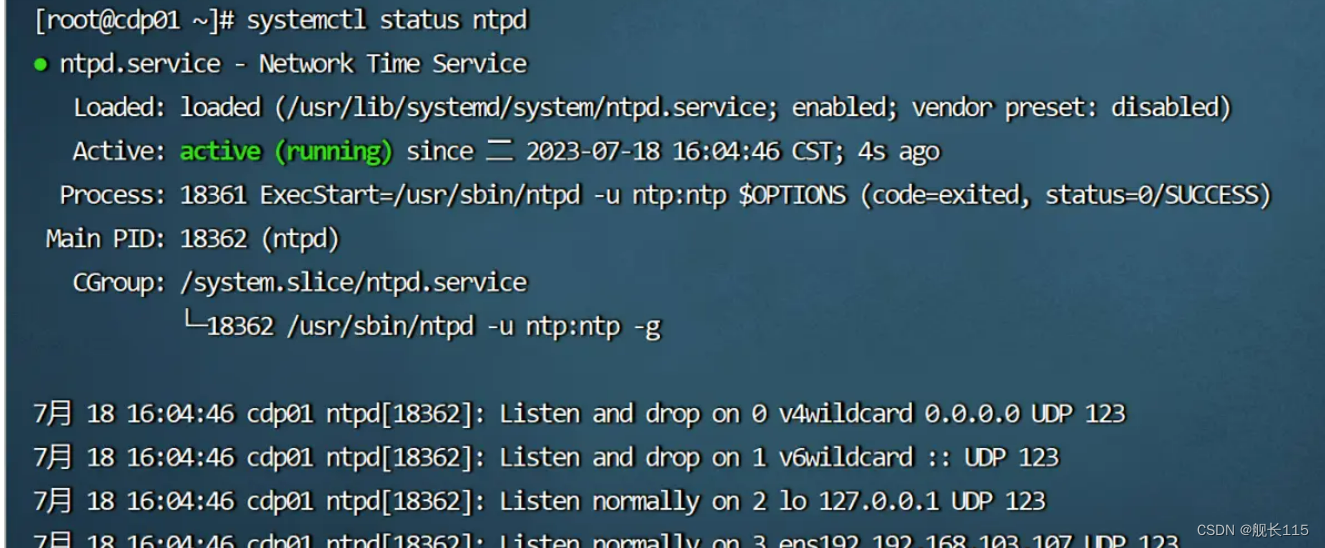
3、然后,重启ntpd服务。
systemctl restart ntpd4、再次查看服务状态,已显示正常。 systemctl status ntpd