企业网站建设需求调查网站备案 查询
一、inand 驱动问题的解决
1、先从现象出发定位问题
(1) 解决问题的第一步,是定位问题。所谓定位问题,就是找到源代码当中导致这个问题的那一句或者那几句代码。有时候解决这个问题需要修改的代码和直接导致这个问题的代码是不同的。我们这里说的定位问题指的是,定位到出问题的代码处,也就是运行了这一句代码时发生了这个错误。
(2) 定位了问题之后,实际修改程序解决问题不一定改的是这一句代码。但是肯定和这一句代码有关联,我们要通过自己分析来找到这种关联,从而从定位的错误点找到真正需要修改的点,然后去修改他。
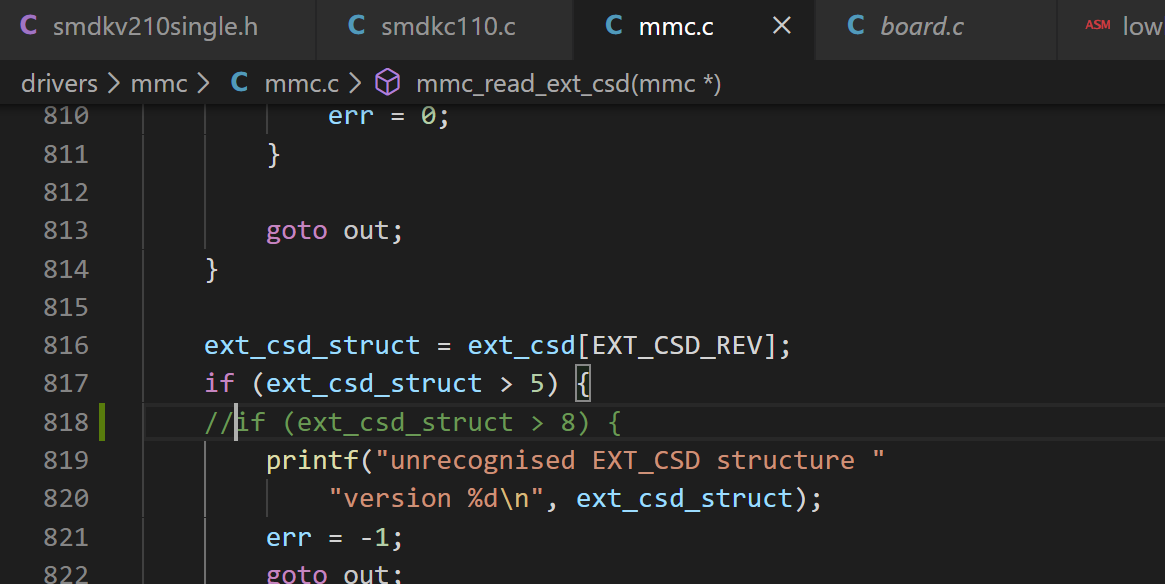
(3) 实战方法:从打印出来的错误信息中挑选一个关键词,然后去源代码中搜索这个关键字,通过这种搜索的方法定位问题。通过搜索将问题定位在 drivers/mmc/mmc.c 的 818 行。
(4) 然后就是解决问题了。
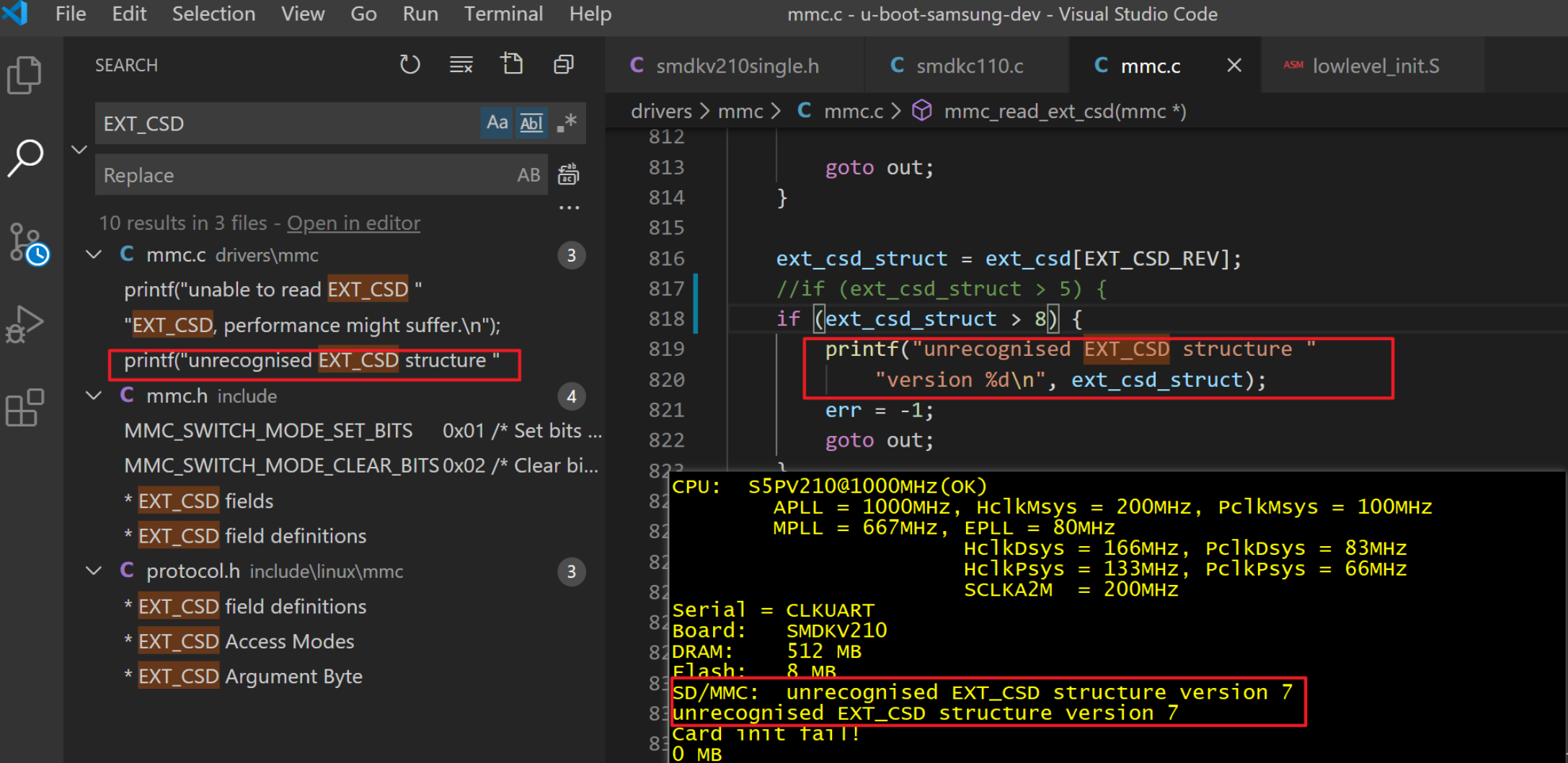
2、网络搜索解决方案
(1) 初步的解决方案是自己先浏览一遍这个问题点周边代码的上下文。通过浏览代码上下文,发现这个函数是在读取 SD/iNand 的 ext_csd 寄存器的值。通过浏览代码,结合出错地方,可以判断出:从卡端读取 ext_csd 寄存器是成功的,并且从读取结果中拿到了卡的版本号信息。然后代码对版本号进行了判断,并且如果版本号大于 5 就会报错,并且函数错误退出。这就是问题所在。
(2) 问题就是:我们使用的 iNand 卡的版本号大于 5,而 uboot 代码本身不处理版本号大于 5 的卡,因此出错了。
(3) 怎么解决?第一可能,换卡;第二可能,软件修复。
(4)网络搜索错误关键字,然后逐个去查阅,看看哪个可以给我们提供解决问题的思路和方法。http://blog.csdn.net/wang_shuai_ww/article/details/22308853
3、尝试修改代码解决问题
(1) 解决方法就是修改 uboot 中的代码,把判断的 5 改成更大的数字。譬如 8,然后跳过这个错误。

现象:
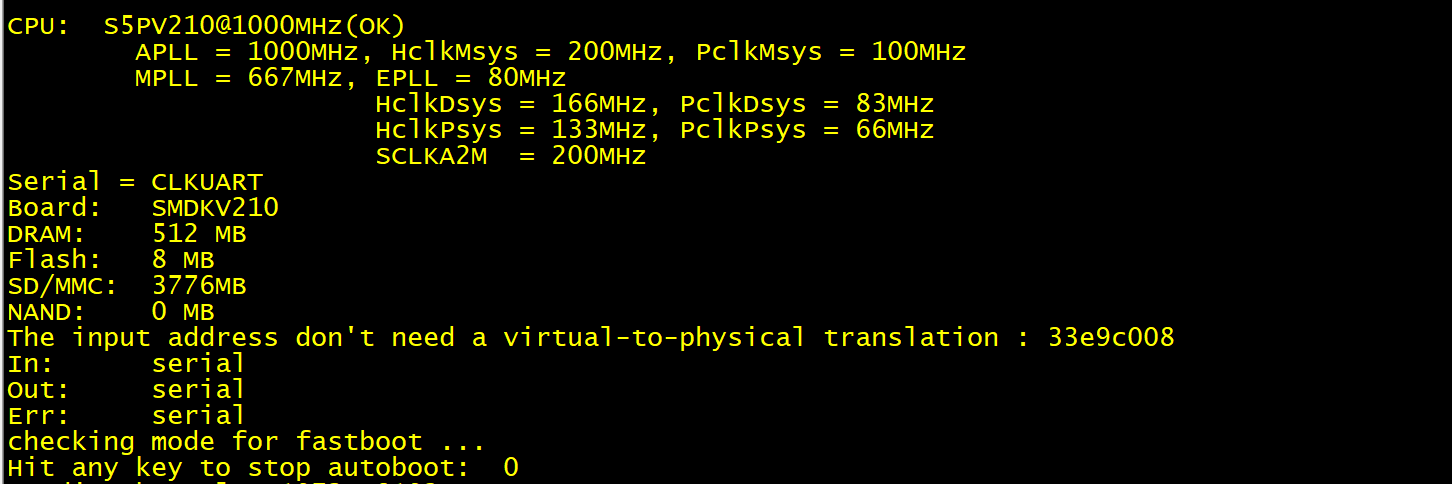
4、推测和实验验证(SD卡和iNand的区别)
(1) 当前板子上有一个 iNand 接在 SD0 上,有一个外置 SD 卡接在 SD2 上。那 uboot 中初始化的这个是 iNand 而不是 SD 卡。也就是说,uboot 中实际用的是 SD0, 而不是SD2.
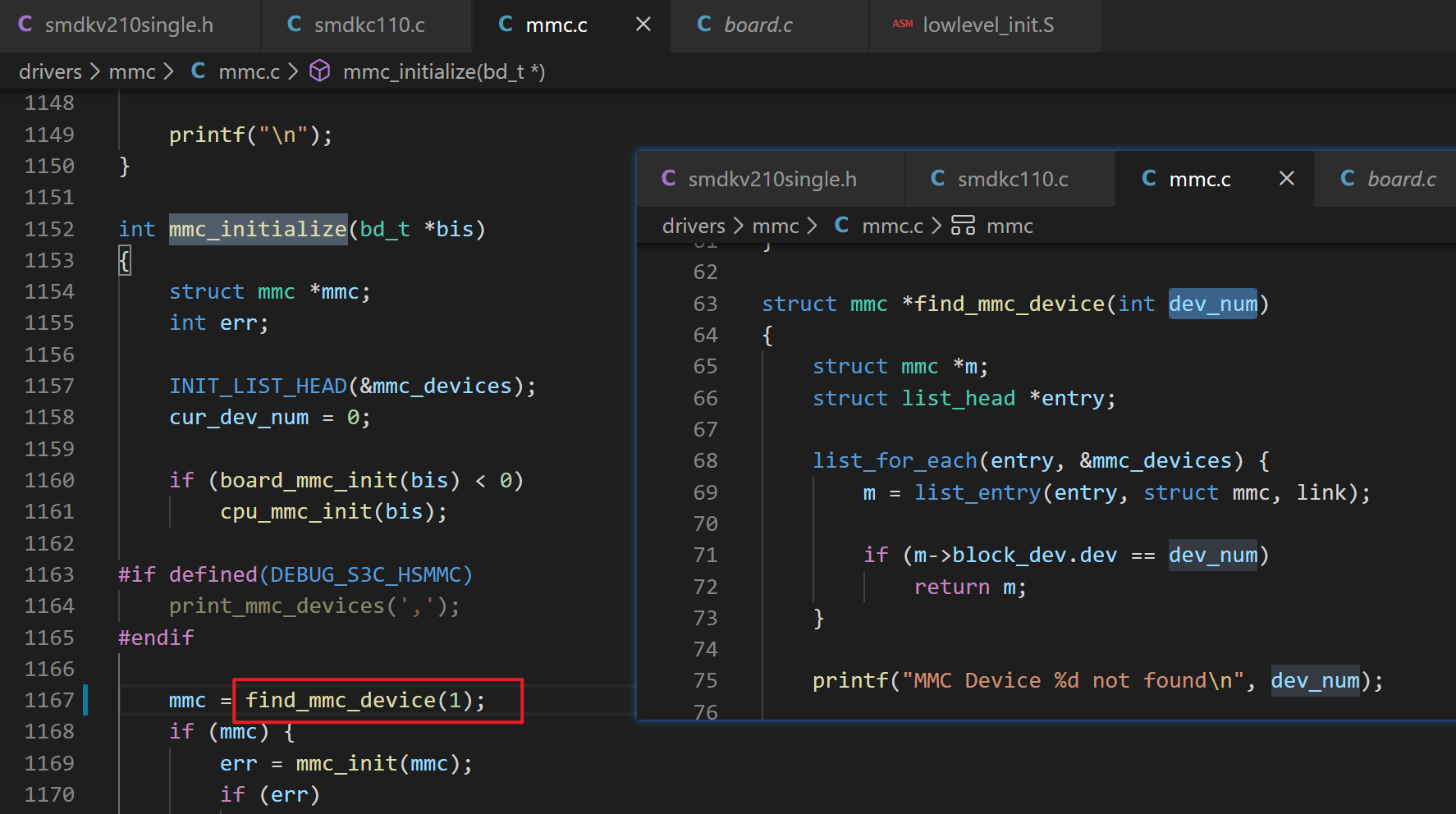
现象:
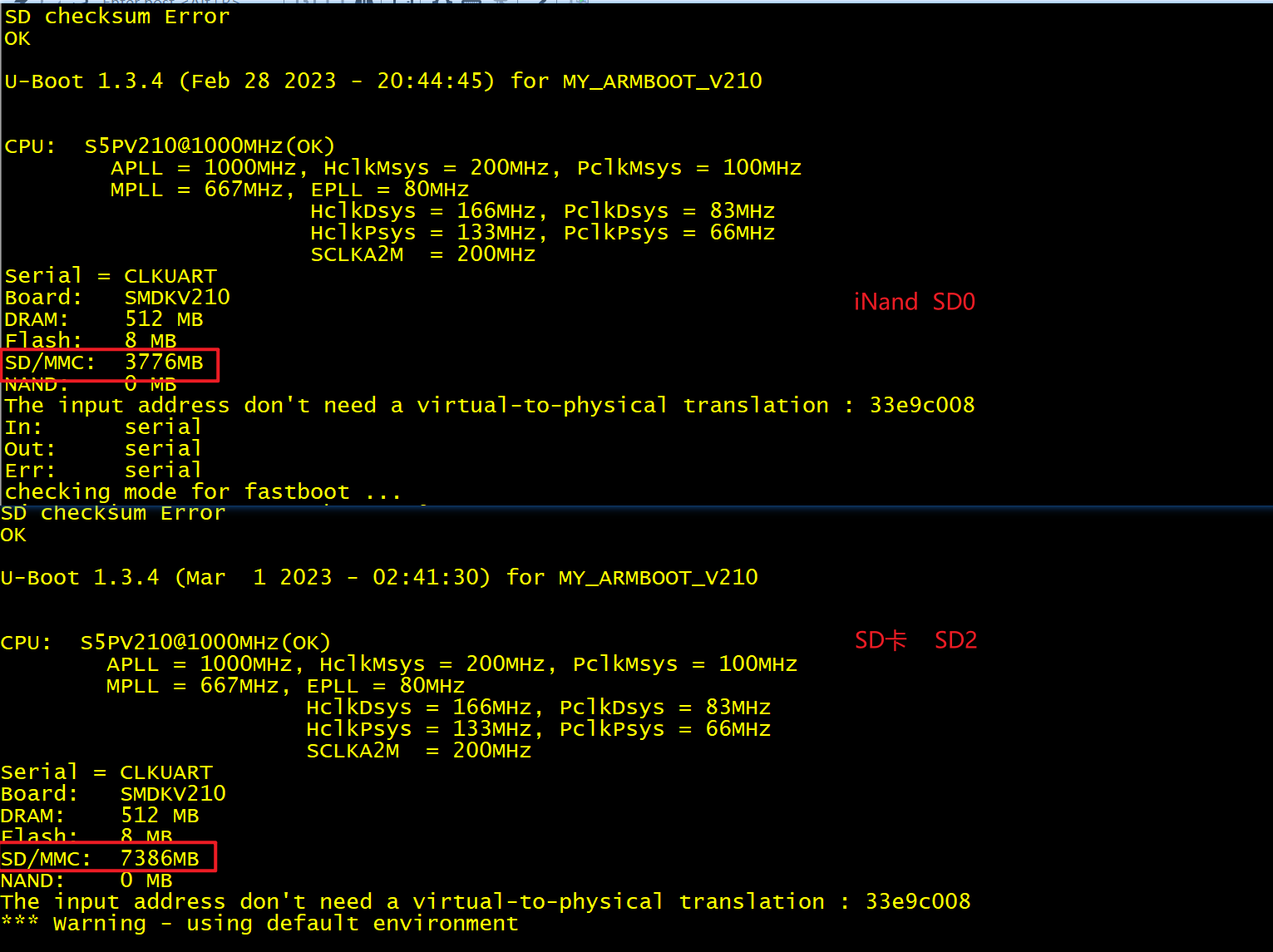
完整的现象截图:
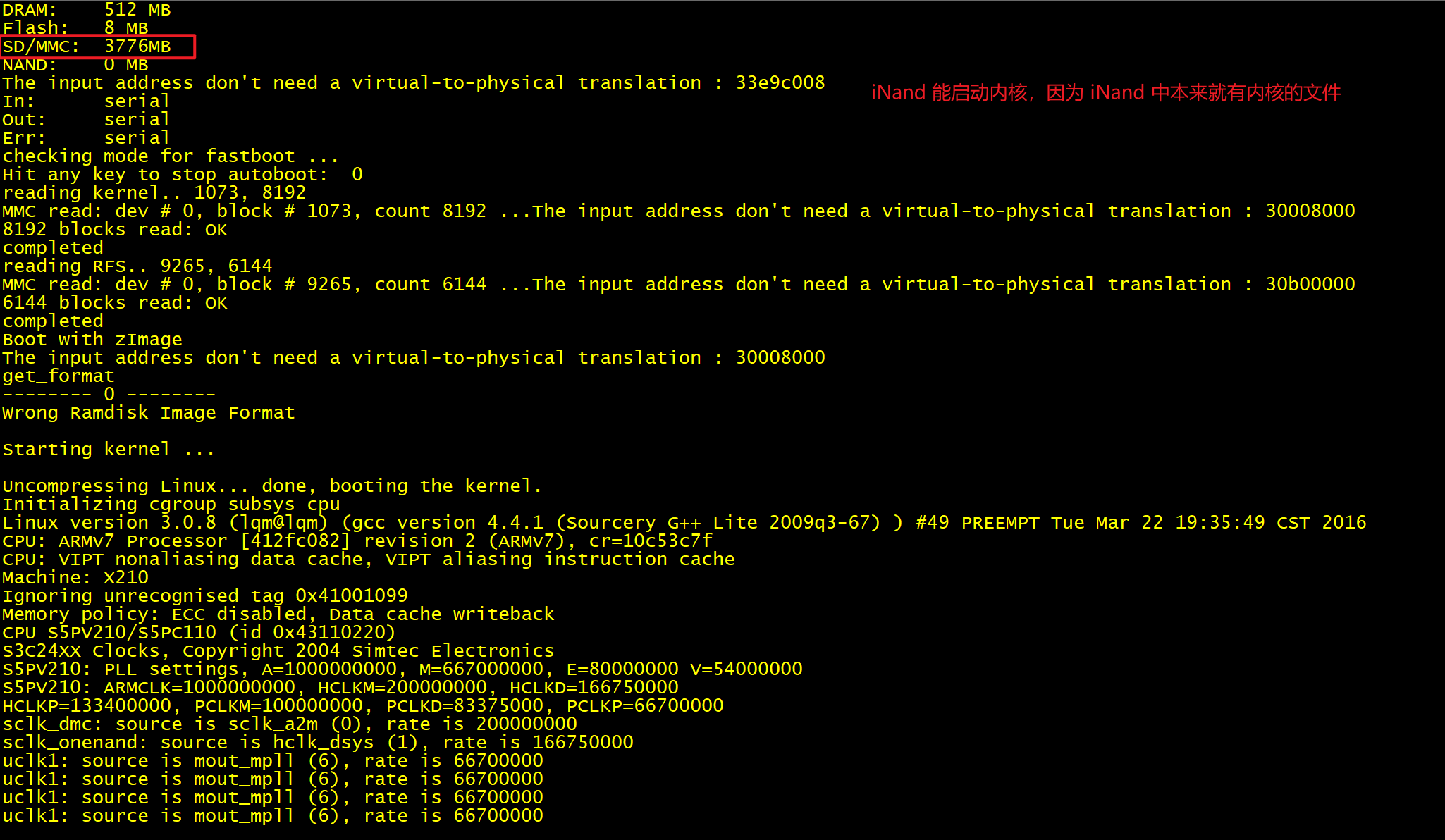
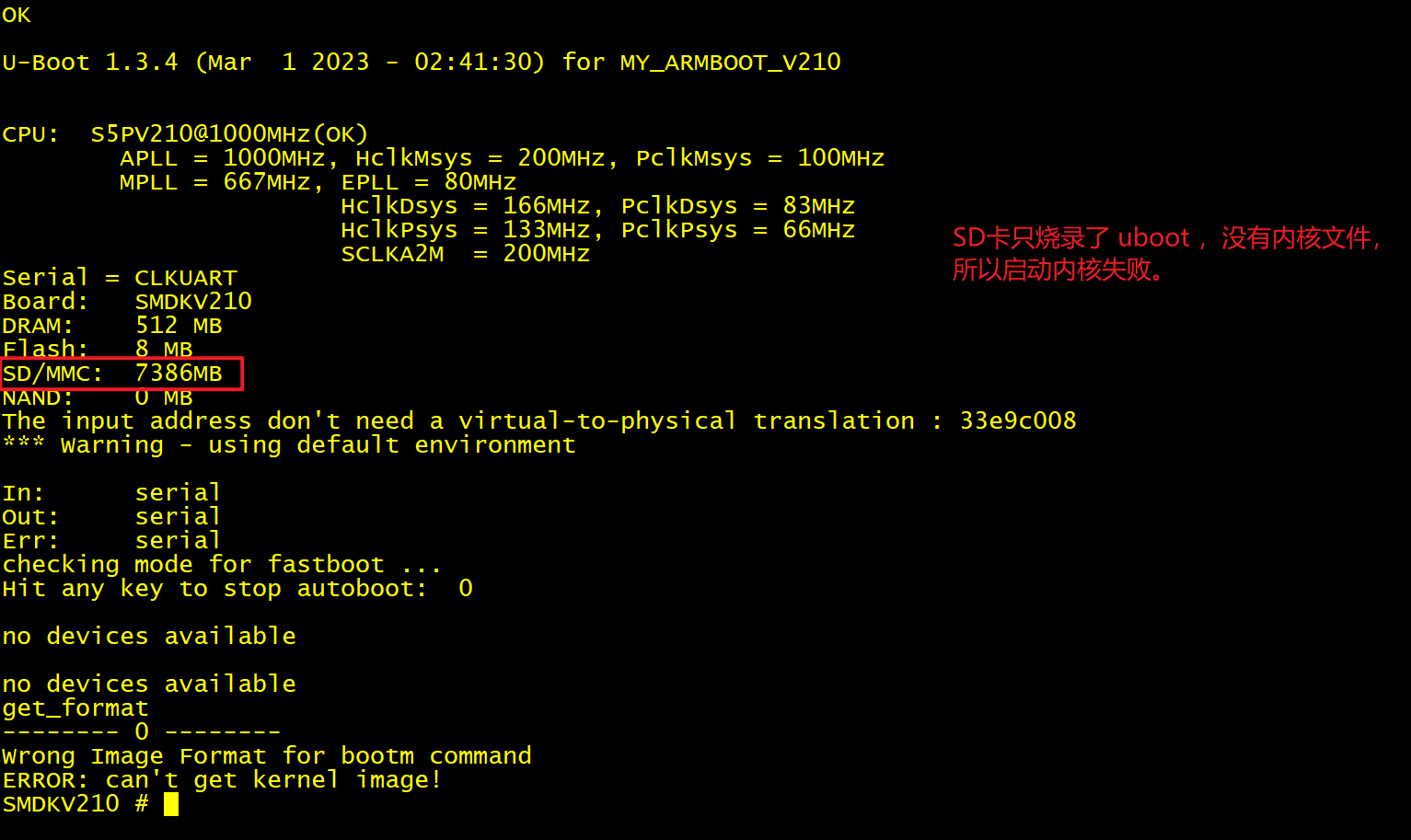
(2) 大家可以尝试,使用外置 SD 卡时,这个版本号的问题不会出现。从这里可以推测出,SD 卡和 iNand 的区别,至少从一个角度可以看出:SD 卡版本低,iNand 的版本比较高。
二、一些小问题的修补
1、控制台串口更换为串口 0
(1) uboot 中默认使用串口 2 来做控制台输入输出的。
(2) SOC 中一共有 4 个串口(串口 0、1、2、3),开发板 X210 上用 DB9 接口引出了 2 个串口,分别是串口 2 和串口 0.(靠边的是串口 2,靠里那个是串口 0)。
(3) 三星公司推荐使用串口 2 来作为调试串口,所以在三星移植的 uboot 和内核版本中都是以串口 2 默认为控制台串口的。
(4) 有时候项目需要将调试串口修改为另外的串口(譬如串口 0),这时候需要修改 uboot 的代码,做移植让 uboot 工作在串口 0 的控制台下。
(5) uboot 中真正去硬件初始化串口控制器的代码在 lowlevel_init.S 中的 uart_asm_init 中,其中初始化串口的寄存器用 ELFIN_UART_CONSOLE_BASE 宏作为串口 n 的寄存器的基地址,结合偏移量对寄存器进行寻址初始化。所以 uart_asm_init 中到底初始化的是串口几(从 0 到 3)?取决于 ELFIN_UART_CONSOLE_BASE 宏。这个宏的值又由 CONFIG_SERIALn(n 是从 1 到 4)来决定。
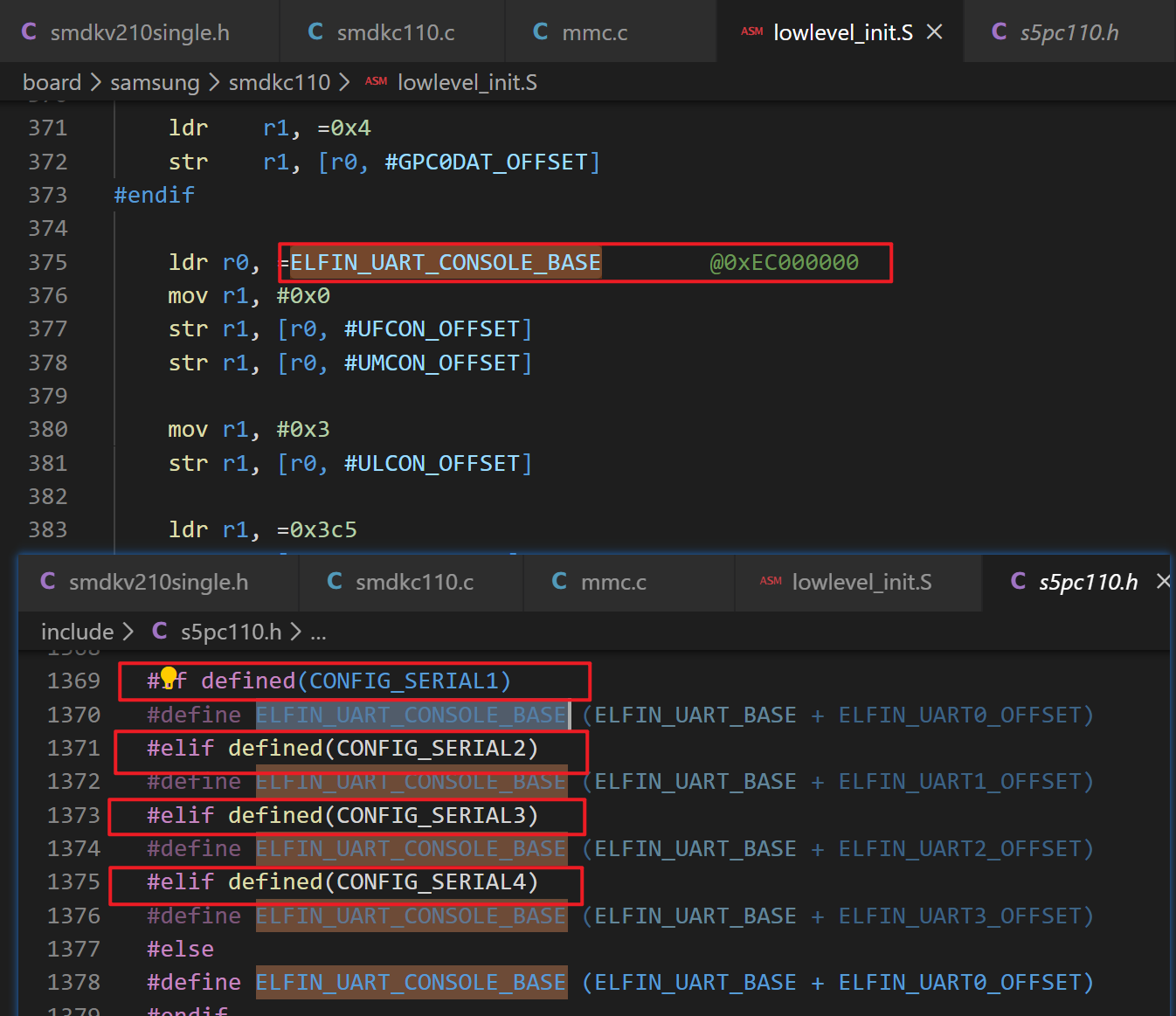
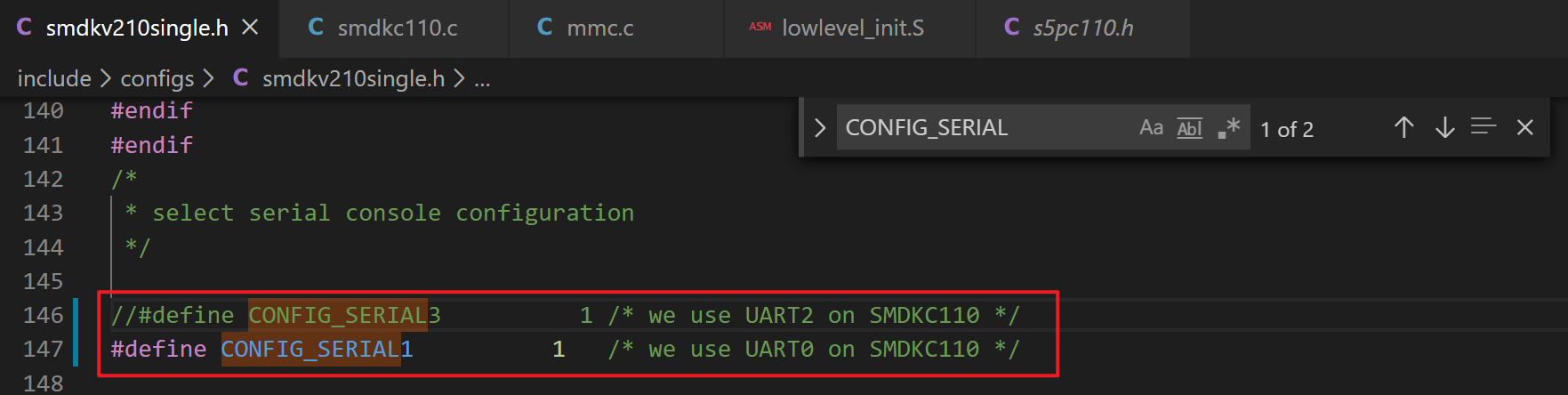
(6) 同步代码、编译烧录运行,发现串口线插在串口 2 上,控制台上只打印:SD checksum error.(这个是内部 iROM 打印出来的,内部 iNand 校验失败的信息);然后将串口线改插到串口 0 上,启动,所有的信息出现。实验成功。
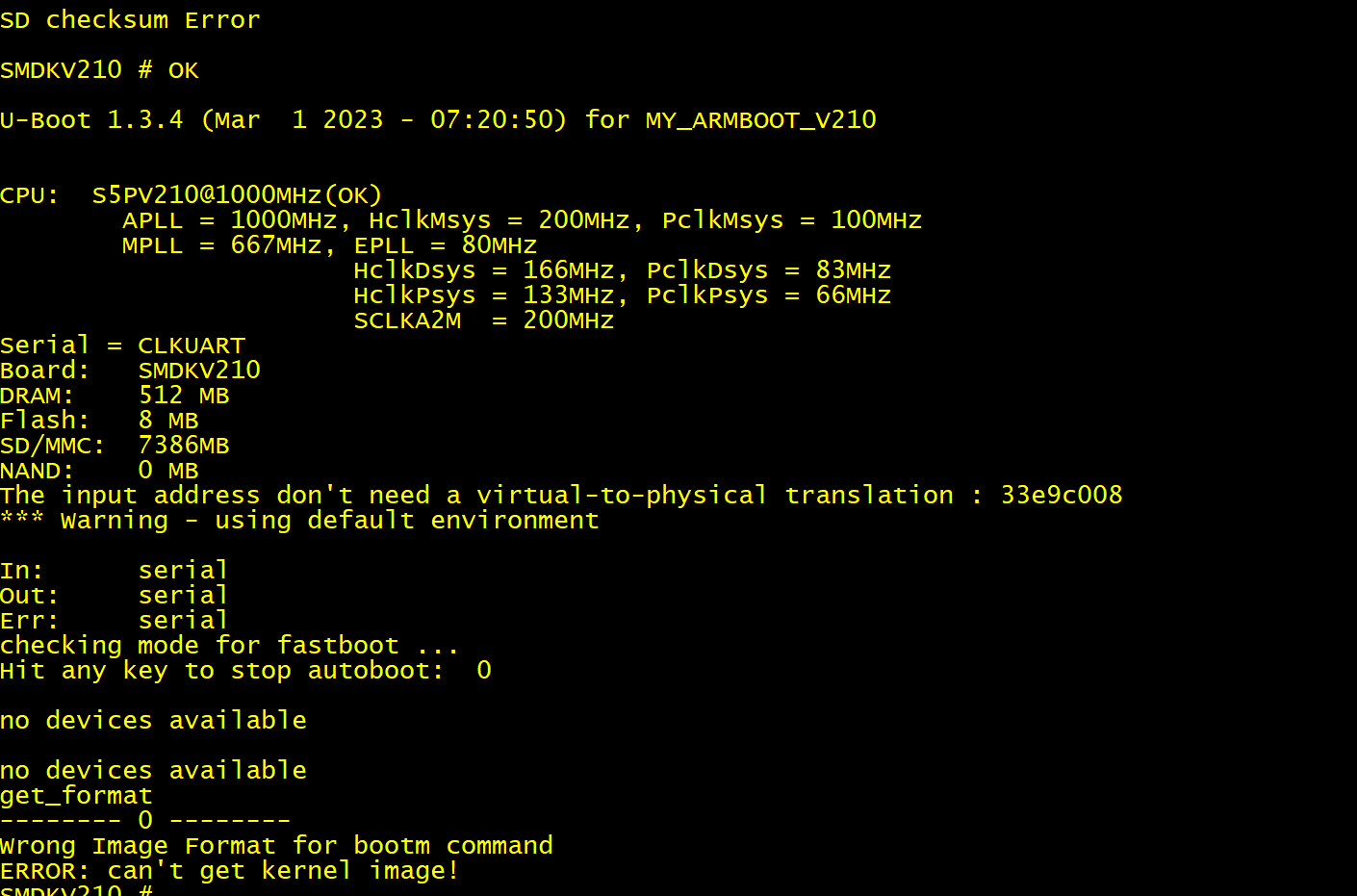
2、修改默认网络地址设置
(1) 修改配置头文件 smdkv210single.h 中的 CONFIG_IPADDR 等宏,则可以修改 uboot 的默认环境变量。
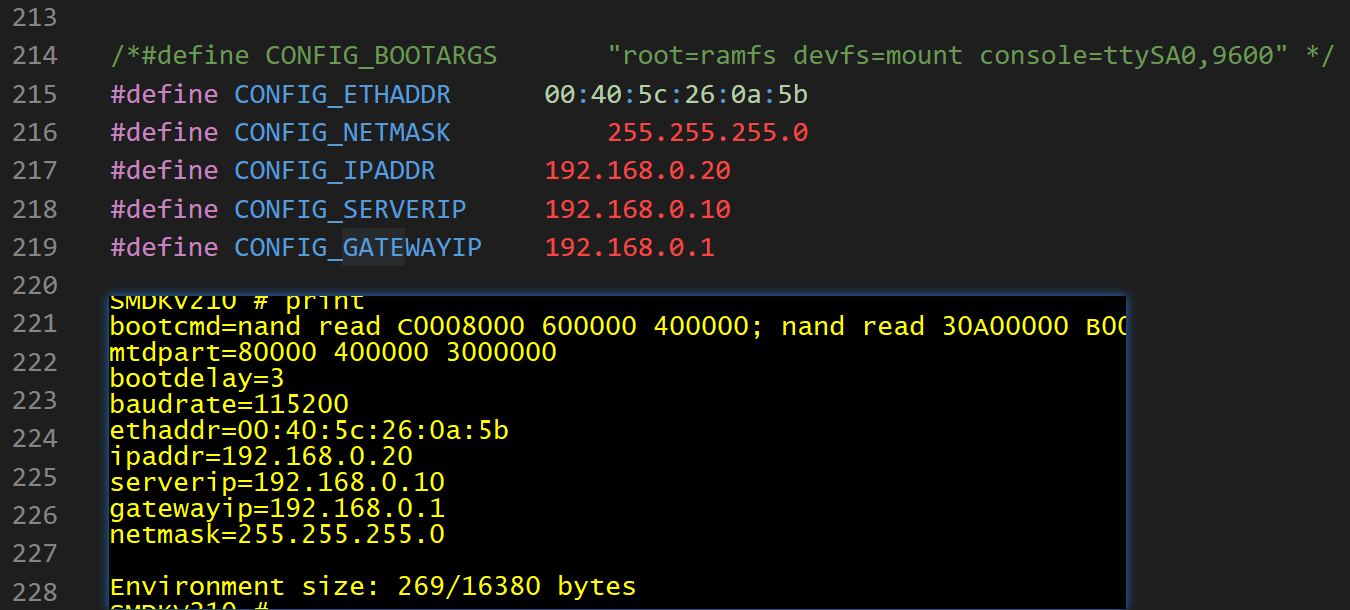
修改后:
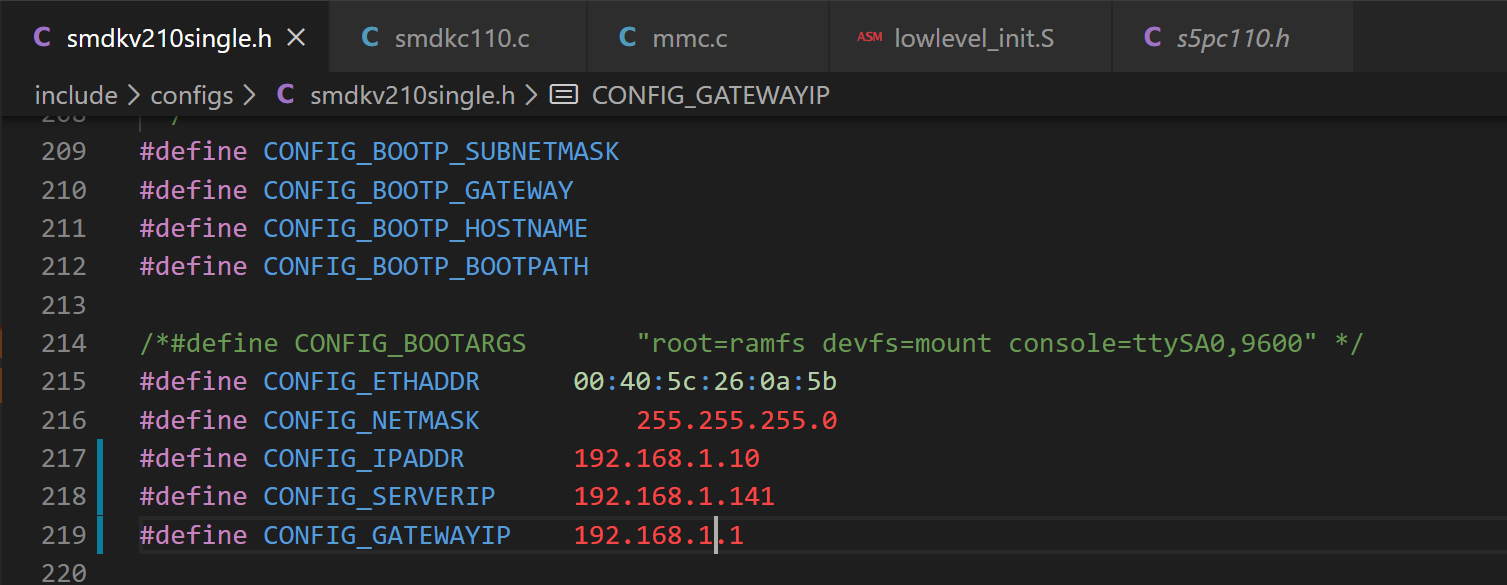
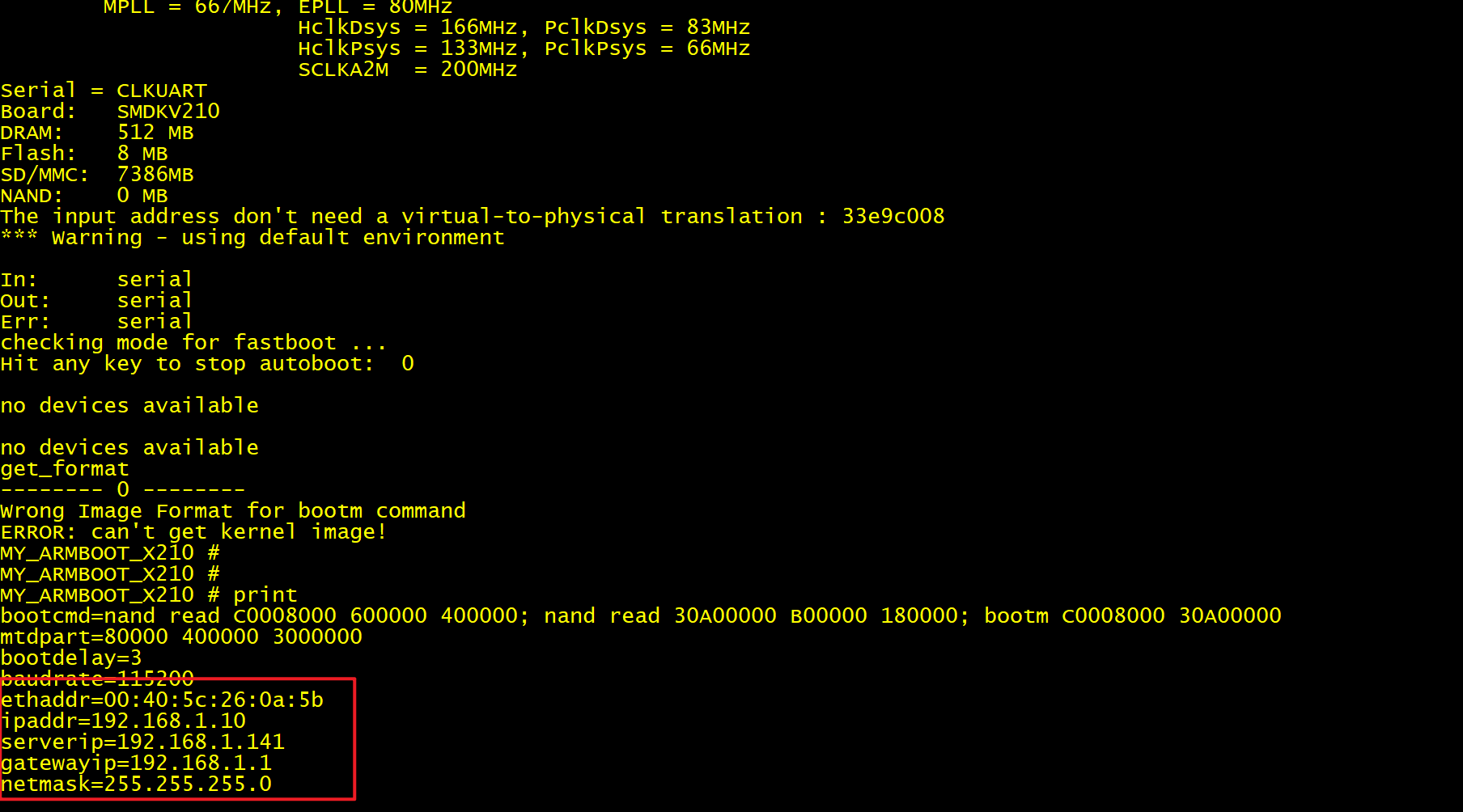
(2) 更改完成后,如果环境变量还是原来的,正常。因为原来 uboot 执行过 saveenv,因此环境变量已经被保存到 iNand 中的 ENV 分区中去了。uboot 启动后校验时 iNand 的 ENV 分区中的环境变量是正确的,因此会优先加载。我们在 uboot 源代码中修改的只是默认的环境变量。
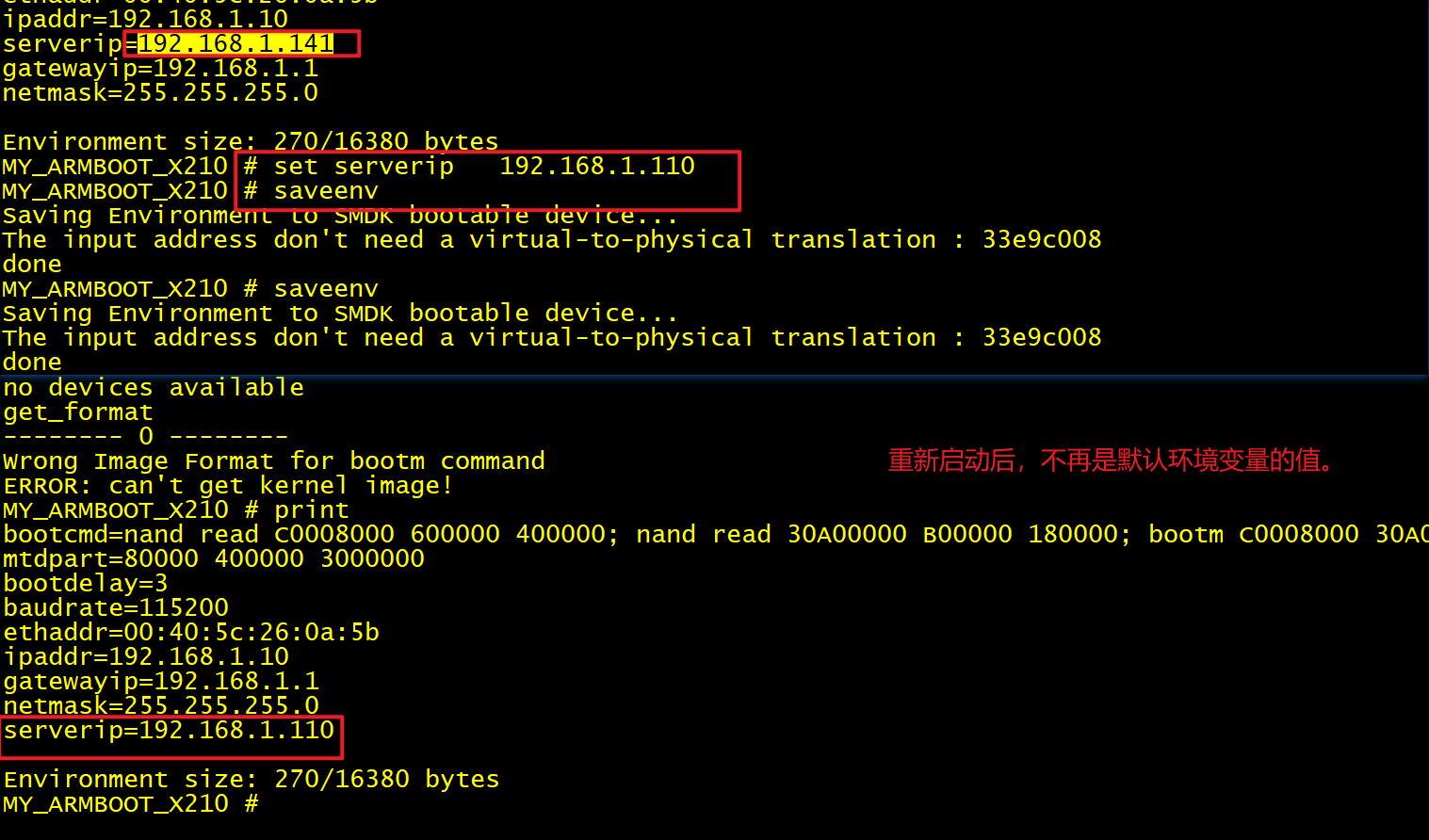
解决方案是擦除掉 iNand 中的那一份环境变量,然后迫使 uboot 启动时,使用 uboot 代码中自带的默认的这一份环境变量,就可以看到了。
(3) 可以使用 mmc write 0 30000000 11# 32(表示将 DDR 的 0x30000000 开头的一段内存中的内容,写入 iNand 中的第 17 个扇区开始的 32 个扇区内,写入长度是 32 个扇区长度(16KB))
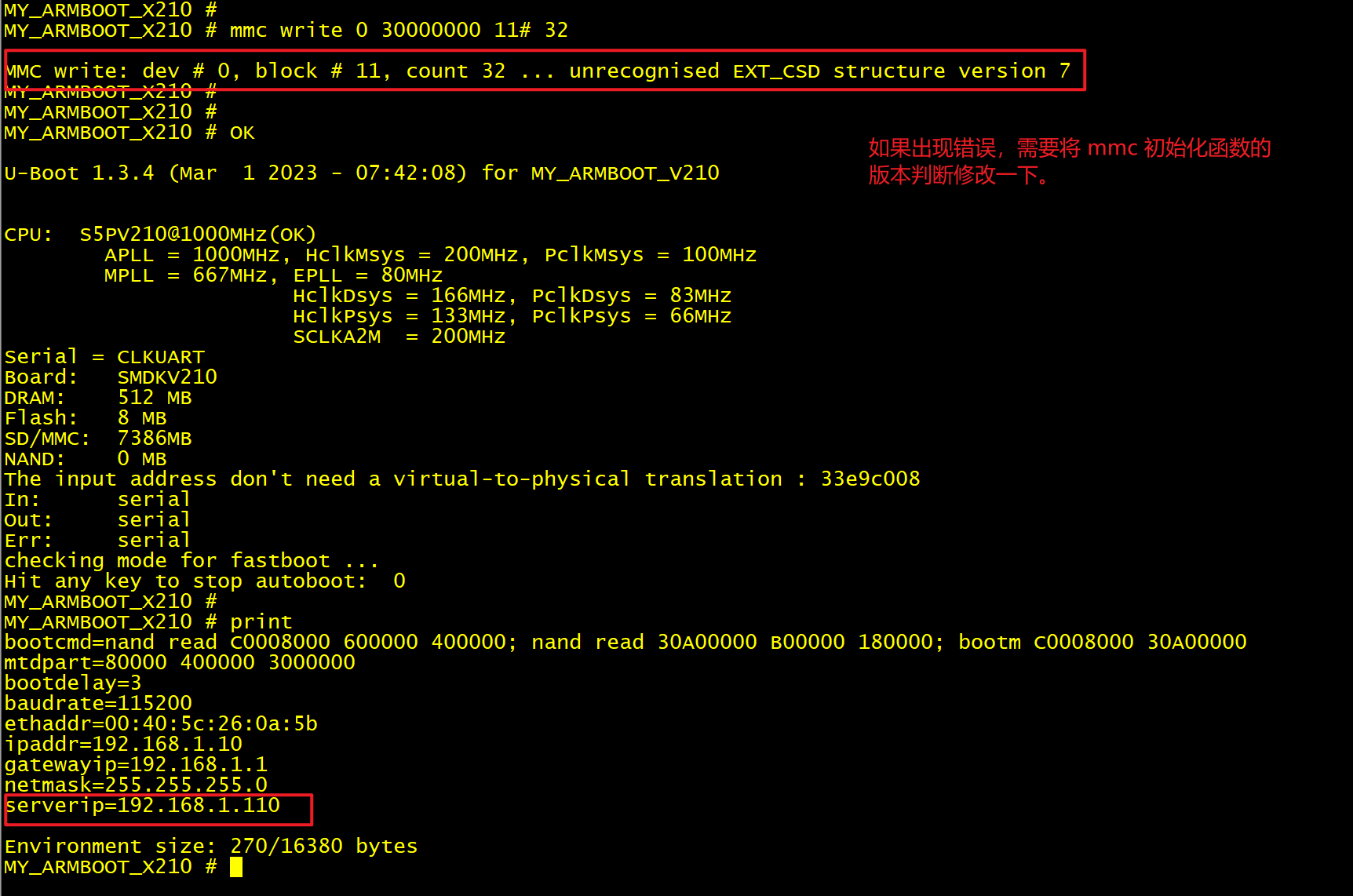
3、修改行提示符
(1)


三、网卡驱动移植1
1、网卡芯片与开发板的连接方式
(1) SoC 的 SROM bank, 和网卡芯片的 CS 引脚( SROM 就是 SRAM/ROM)。
SoC 的 SROMController, 其实就是 SoC 提供的 对外总线式连接 SRAM/ROM 的接口。如果 SoC 要外部外接一些 SRAM/ROM 类的存储芯片(或者伪装成 SROM 接口的芯片,譬如网卡芯片),就要通过 SROM Controller 来连接。网卡接在 SROM 中的好处就是,网卡芯片好像一个存储芯片一样,被扩展在 SoC 的一个地址空间中,主机 SoC 可以直接用一个地址来访问网卡芯片的内部寄存器。

(2) 网卡芯片内部寄存器使用相对地址访问。网卡芯片内部很多寄存器有一个地址,这个地址是从 00 开始的,但是实际上,我们 SoC 不能用 0 地址去访问这个网卡的芯片内部寄存器。SoC 访问网卡芯片 00 寄存器时的地址,应该是:起始地址+ 00。 这里的起始地址就是网卡芯片对应接在 SROM bankn 中的 bankn 对应的基地址。
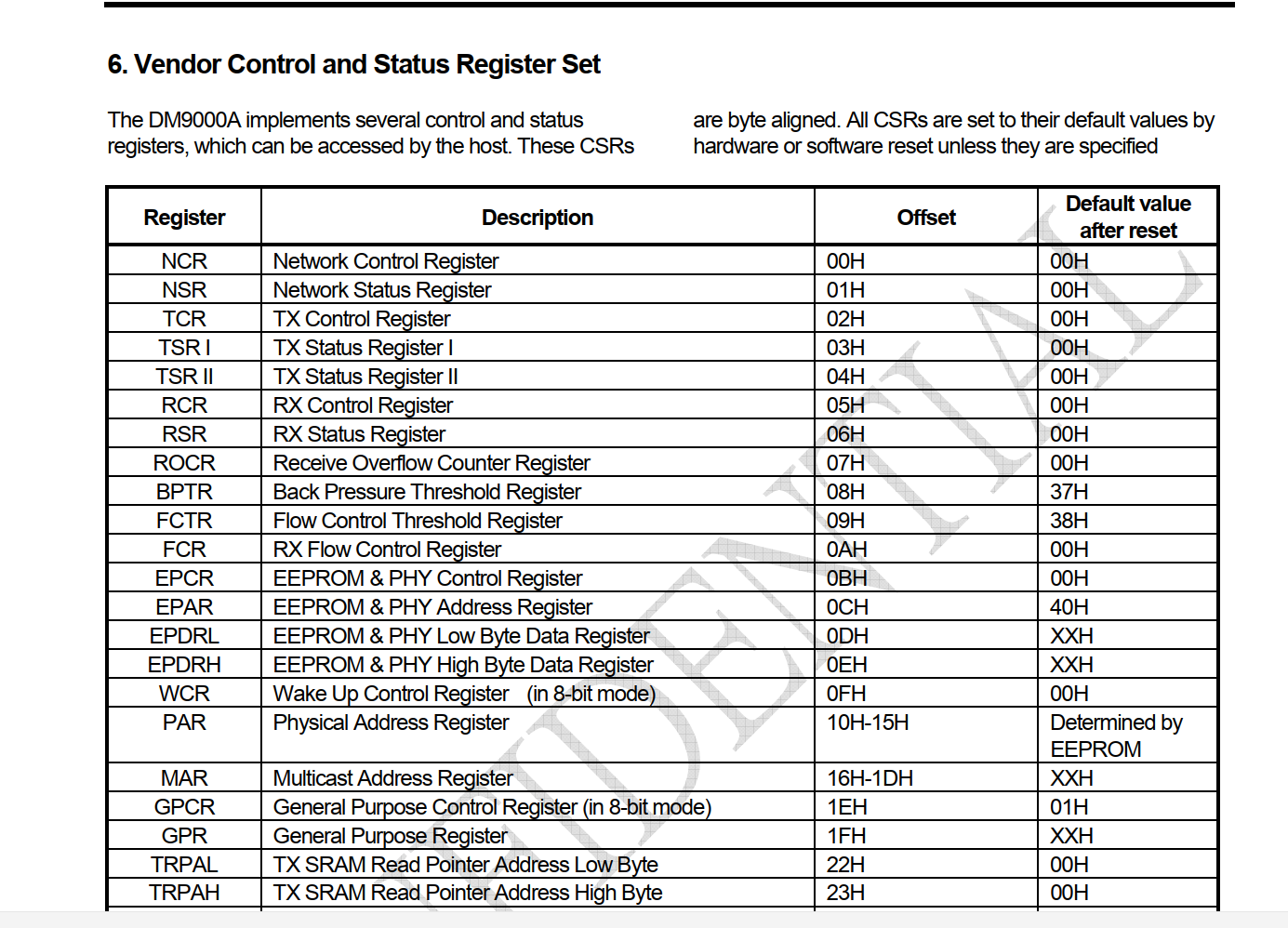
《DM9000AEP.pdf》
(3) 主机 SoC 上网,其实就是通过操控网卡芯片内部的寄存器、缓冲区等资源来上网的。也就是说,其实 SoC 是通过网卡芯片来间接上网的。
(4) 总结:网卡芯片实际上也是一种总线式连接方式。优势是 SoC 内部不需要内置网卡控制器,所有的 SFR 全都在外部网卡芯片中,而且还可以通过地址直接访问(IO与内存统一编址),不用像 Nand/SD 接口一样使用时序来访问。
2、原理图浏览
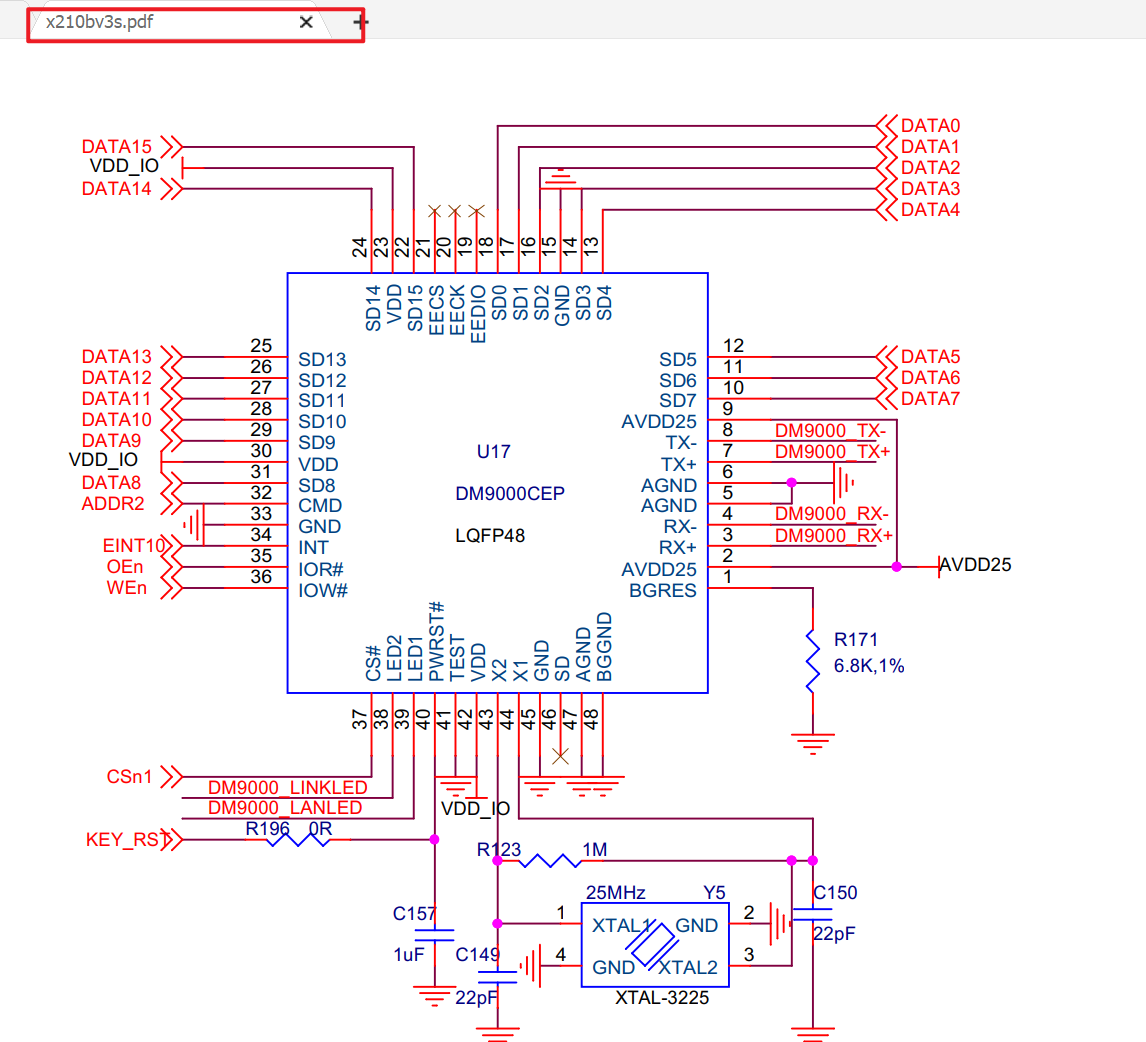
《x210bv3s.pdf》
(1) 210 的 SROM 控制器允许 8/16bit 的接口,我们实际使用的是 16 位接口。

(2) 网线有 8 根线,但是实际只有 4 根有效通信线,另外 4 根都是 GND,用来抗干扰的。4 根通信线中负责发送的有 2 根(Tx- 和 Tx+),负责接收的有 2 根(Rx+ 和 Rx-)。因为网线上传输的是差分信号。
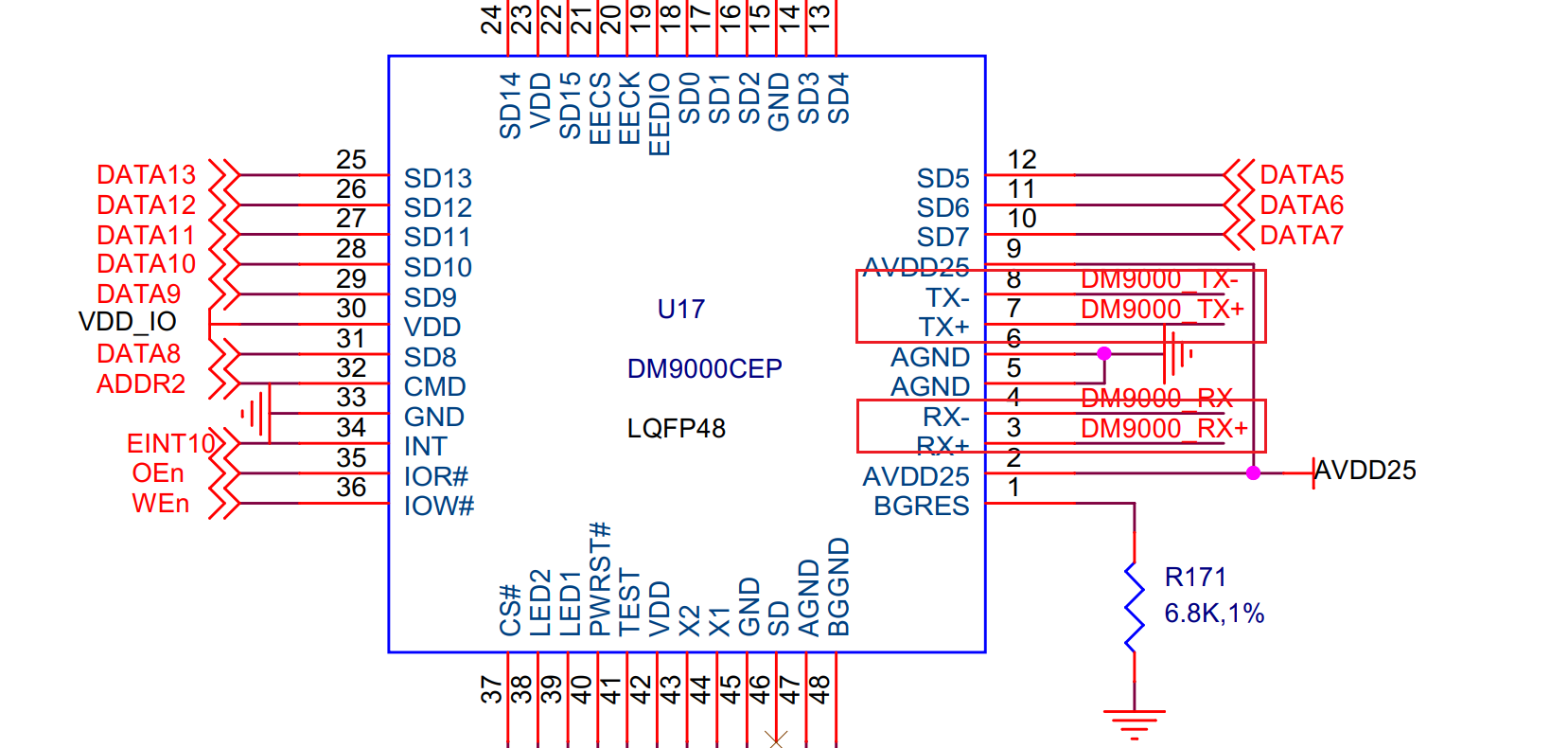
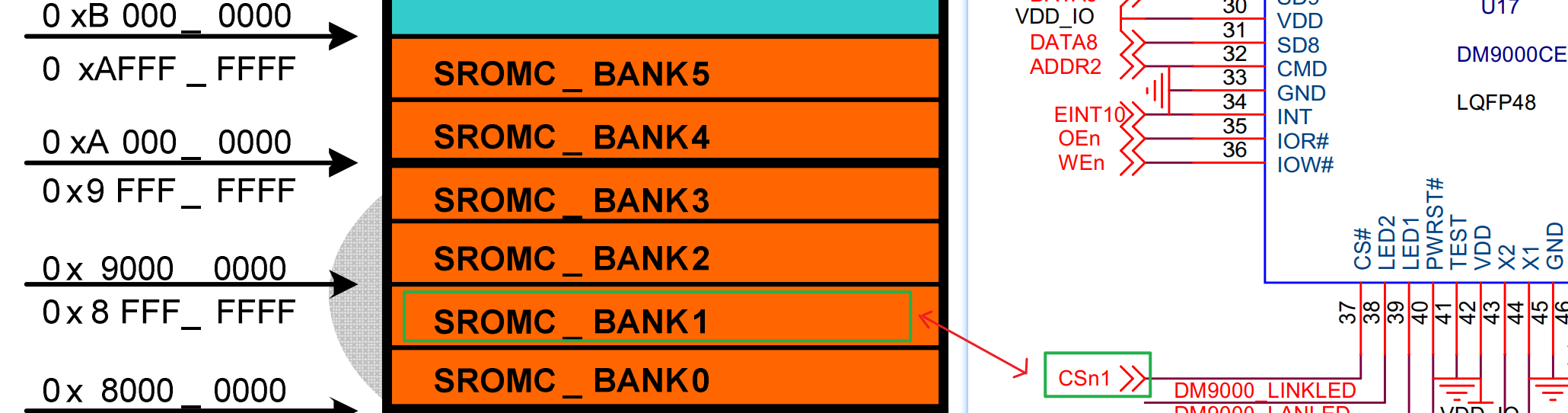
(3) 网卡芯片有个 CS 引脚,(CS 就是 chip select,片选信号,主机向 CS 发送有效信号,则从机芯片工作;主机向 CS 发送无效信号,则从机芯片不工作。),这个引脚要接主机 SoC 的片选信号引脚,主机 S5PV210 的每一个 SROM bank 中有一个片选信号CSn (n=0-5),从原理图可以看出,我们 X210 上将 DM9000 的 CS 引脚接到了 CSn1上,对应 SROM bank1(推断出 DM9000 的总线地址基地址是 0x88000000)。
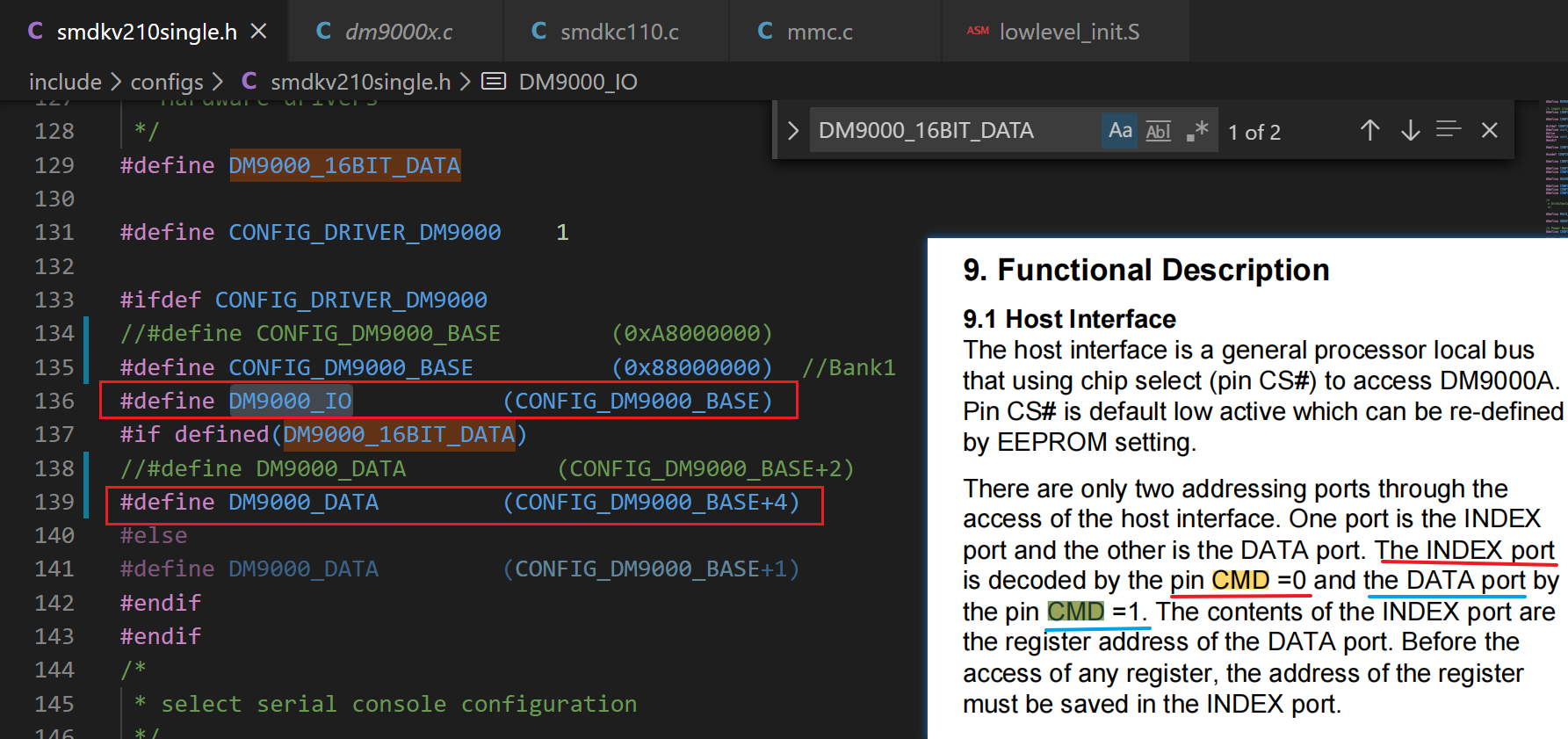
(4) DM9000 的 CMD 引脚,接到了 S5PV210 的 ADDR2 引脚上。DM9000 为了减少芯片引脚数,数据线和地址线是复用的(DATA0 到 DATA15,这 16 根线是有时候做数据线传输数据,有时候做地址线传输地址的。什么时候做什么用,就由 CMD 引脚决定。)通过查询数据手册知道:当 CMD 为高电平时,对应传输是DATA,当 CMD 为低电平时,对应传输为 INDEX(offset,寄存器地址)。
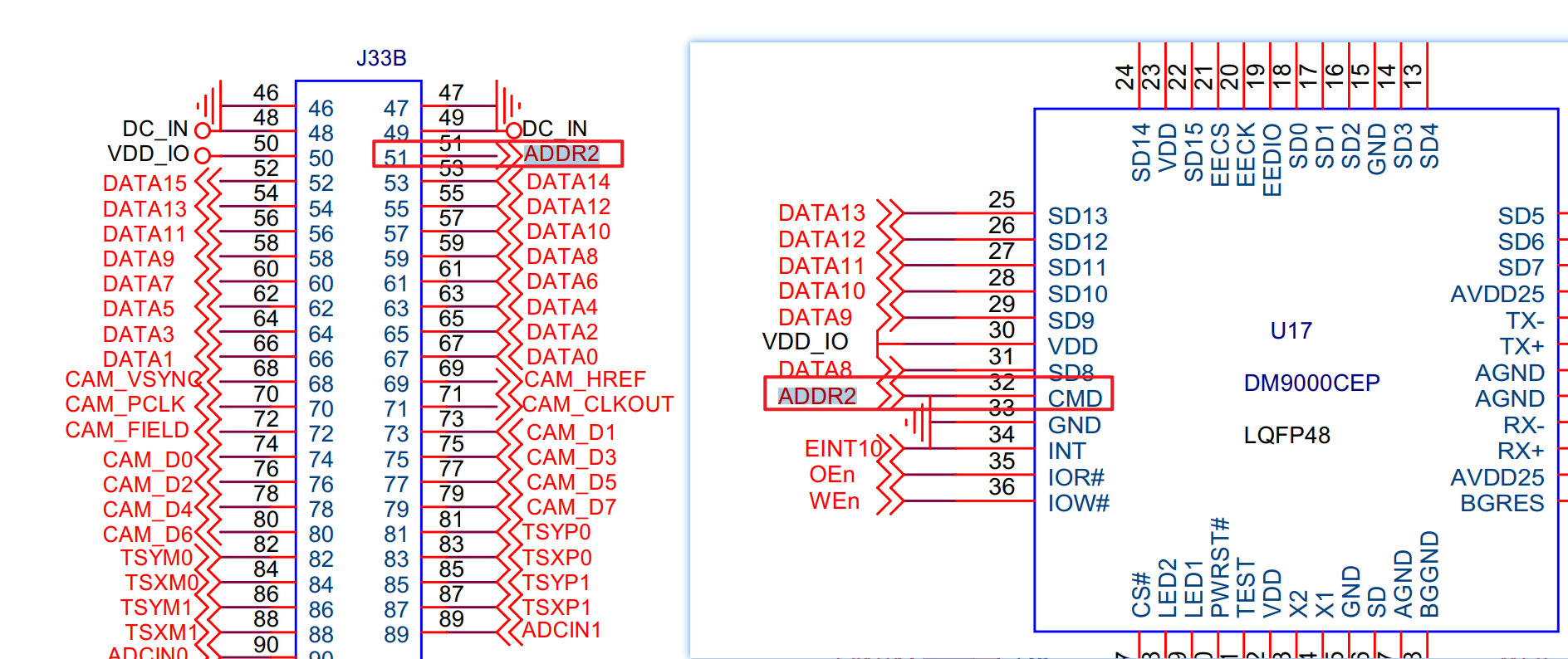

注明:这些引脚上的电平变化都是控制器自动的,不需要程序员手工干预。程序员所需要做的,就是在配置寄存器值时充分考虑到硬件电路的接法,然后给相应寄存器配置正确的数值即可。
四、网卡驱动移植2
1、网卡驱动文件介绍
(1) uboot 中本来就提供了很多网卡芯片的驱动程序,在 uboot/drivers/net/dm9000x.c 和dm9000x.h。
这个驱动来自于 linux kernel 源代码。所以我们 uboot 中是移植而不是编写。
(2) 要想彻底看懂这个驱动,必须对 linux 的驱动模型中网络设备驱动有一定的理解才可以。因为我们还没学驱动,因此这个源代码就不用看了。
(3) 这个驱动是 linux 内核中做好的,根本不用动,可以在 uboot 中直接使用的。而且因为 linux 驱动设计的很合理(数据和代码是分开的,这里驱动主要是代码,数据是由硬件开发板中的接法决定的,数据由一定的数据结构来提供。),所以驱动本身具有可移植性。这个就决定了我们移植 DM9000 驱动时,这个驱动文件 dm9000x.c 和 dm9000x.h 不用动,要动的是数据。
2、网卡移植的关键:初始化
(1) uboot 在第二阶段 init_sequences 中进行了一系列的初始化,其中就有网卡芯片的初始化。这个初始化就是关键,在这里的初始化中,只要将网卡芯片正确的初始化了,则网卡芯片就能工作(意思是网卡驱动 dm9000x.c 和 dm9000x.h 依赖于这里的初始化而工作)。
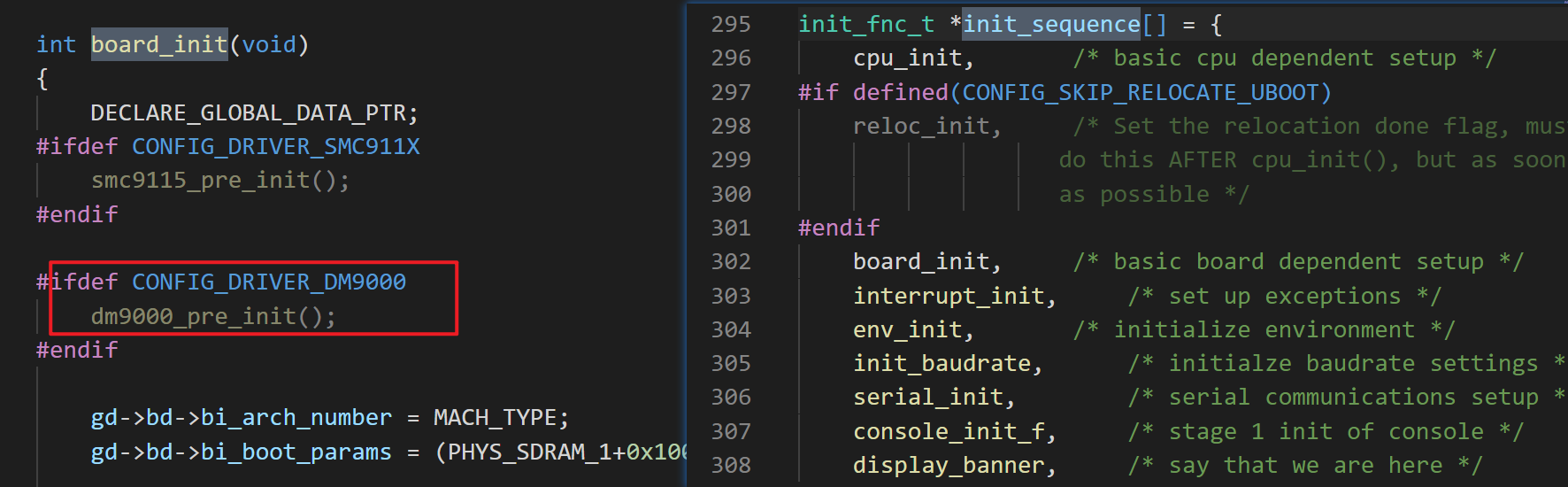
(2) 网卡初始化代码地方在:
start_armbootinit_sequenceboard_initdm9000_pre_init 这个函数就是移植的关键
(3) dm9000_pre_init 函数主要功能就是初始化 DM9000 网卡。这个初始化过程和我们开发板上 DM9000 网卡芯片的硬件连接方式有关。必须要结合开发板原理图来分析,然后决定这个函数怎么编程。
(4) 原来的代码是三星的工程师根据三星的开发板 SMDKV210 的硬件接法来写的程序,我们要根据自己的开发板的硬件接法去修改这个程序,让网卡在我们的开发板上能工作。
(5) #define DM9000_16BIT_DATA 这个宏用来表示 DM9000 工作在 16 位总线模式下。根据上节课的硬件原理图的分析,可以看到我们开发板上 DM9000 确实工作在 16 位模式下。
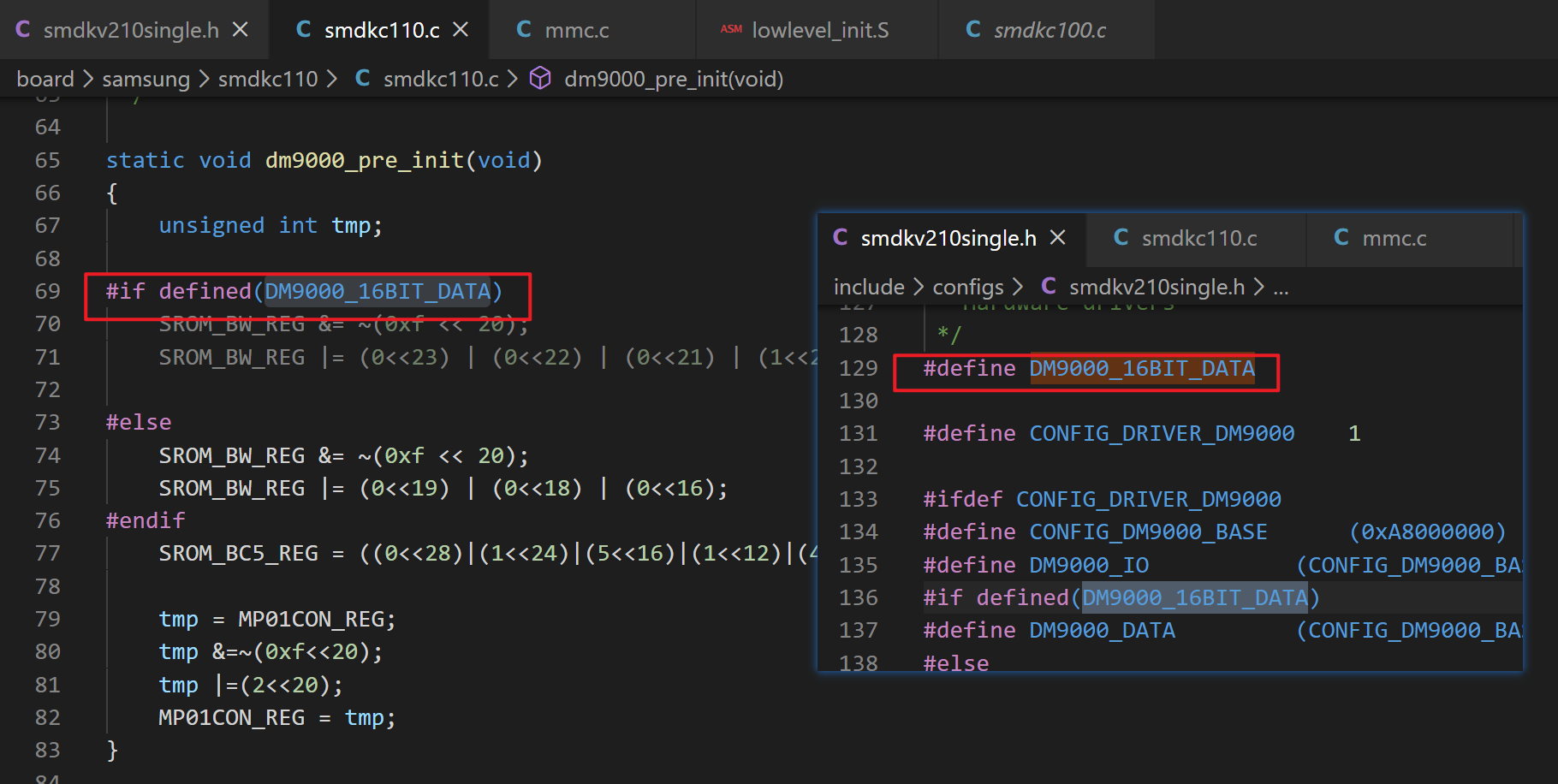
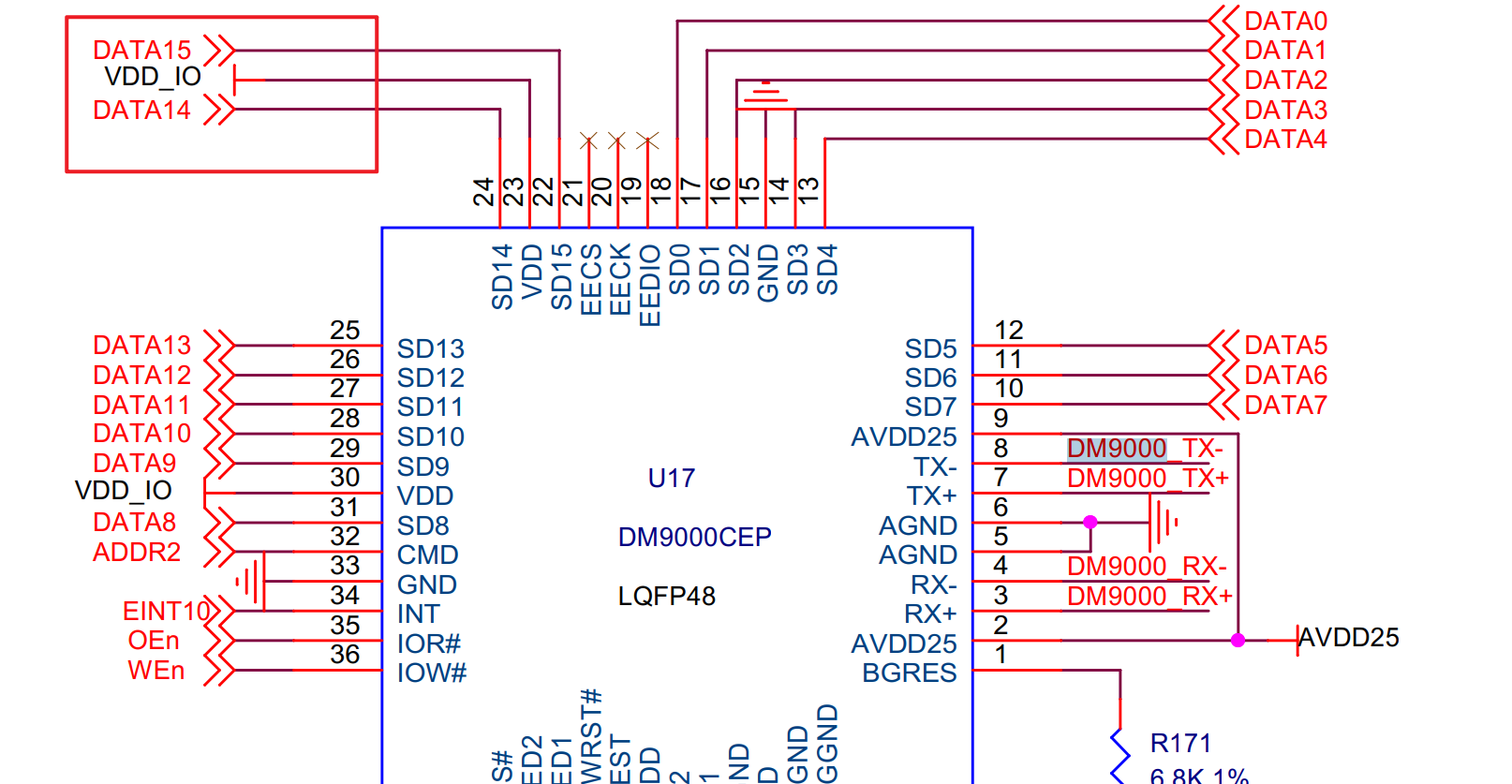
(6) 从三星版本的代码中可以看出,它操作的是 bit20-bit23 ,对照数据手册中寄存器定义,可以看出三星的开发板 DM9000 是接在 Bank5 上的。而我们接在 bank1 上的,因此我们需要操作的 bit 位是 bit4-bit7。

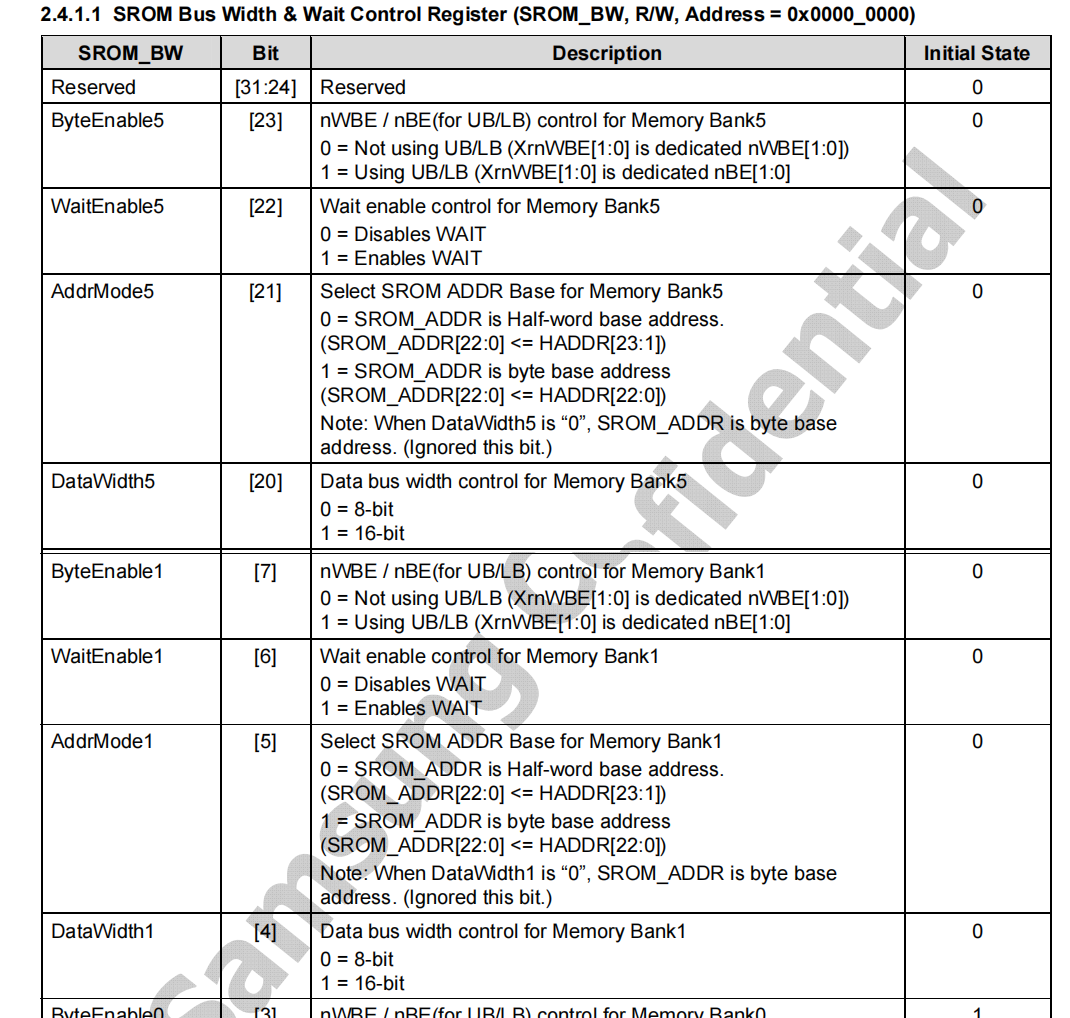
(7) 总结:三个寄存器的修改。主要是三星的开发板DM9000接在bank5,我们接在了bank1上,因此要做一些修改。
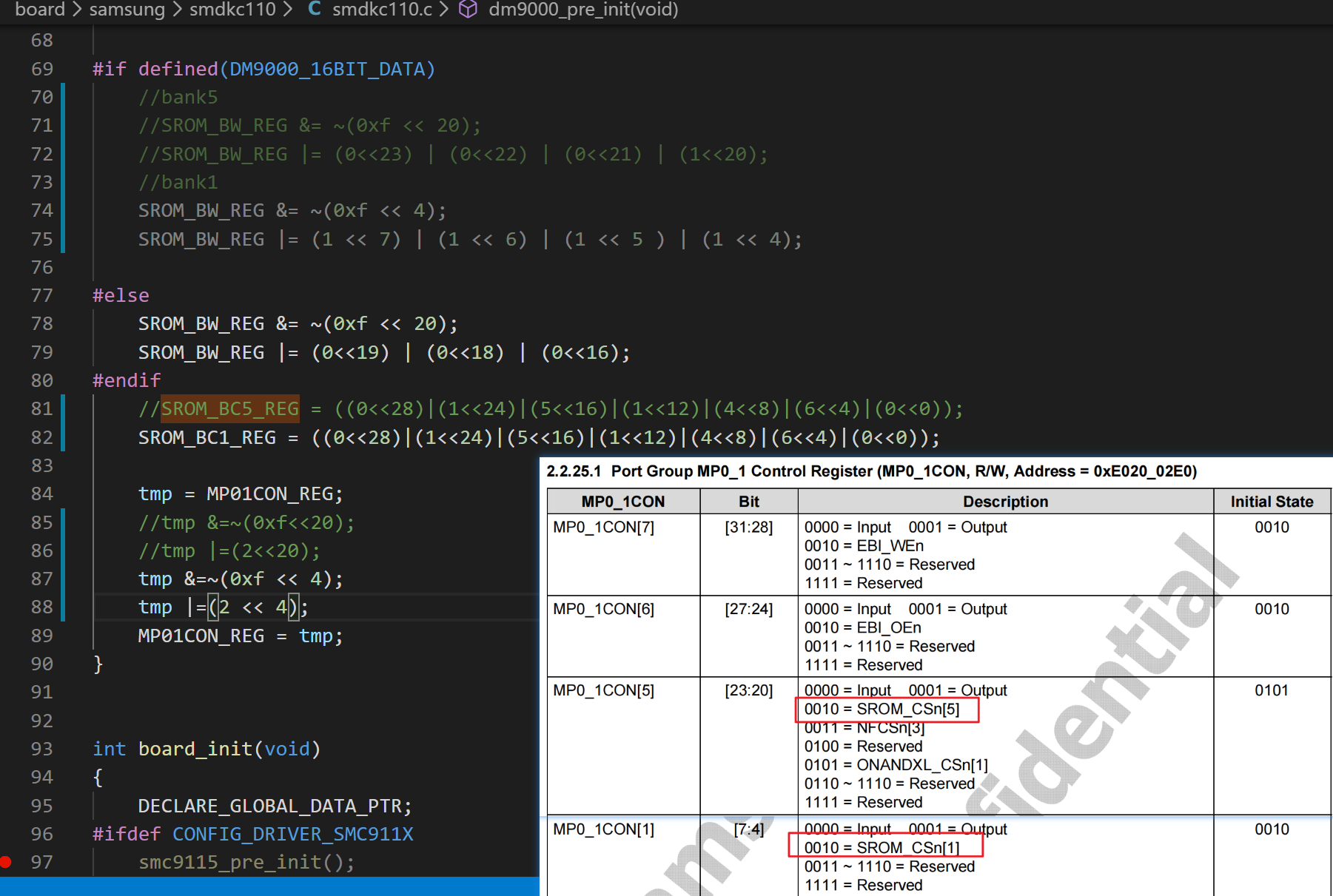
3、基地址的配置等
(1) 之前说过,驱动分为2部分:代码和数据。代码不用动,数据要修改。
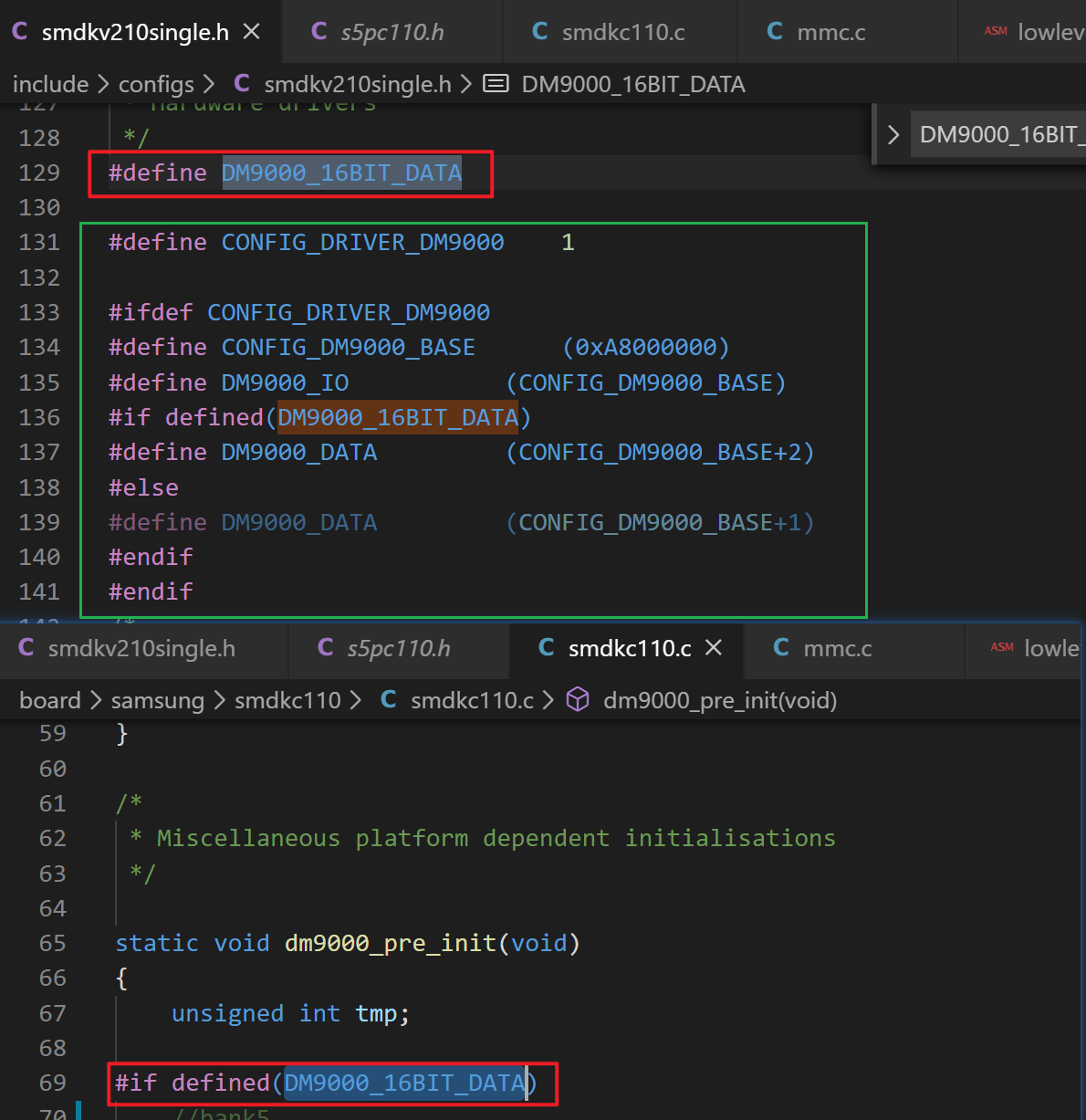
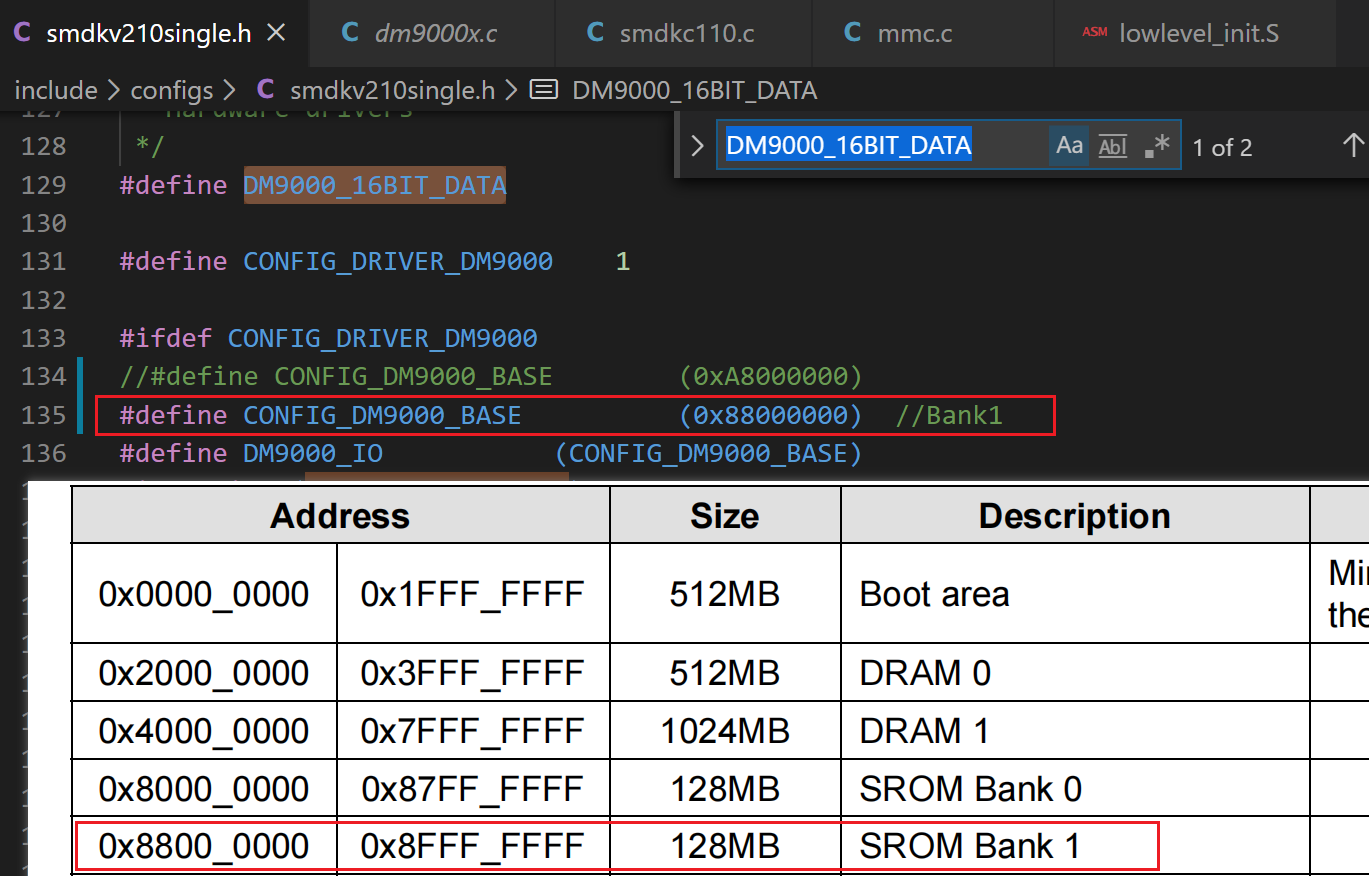
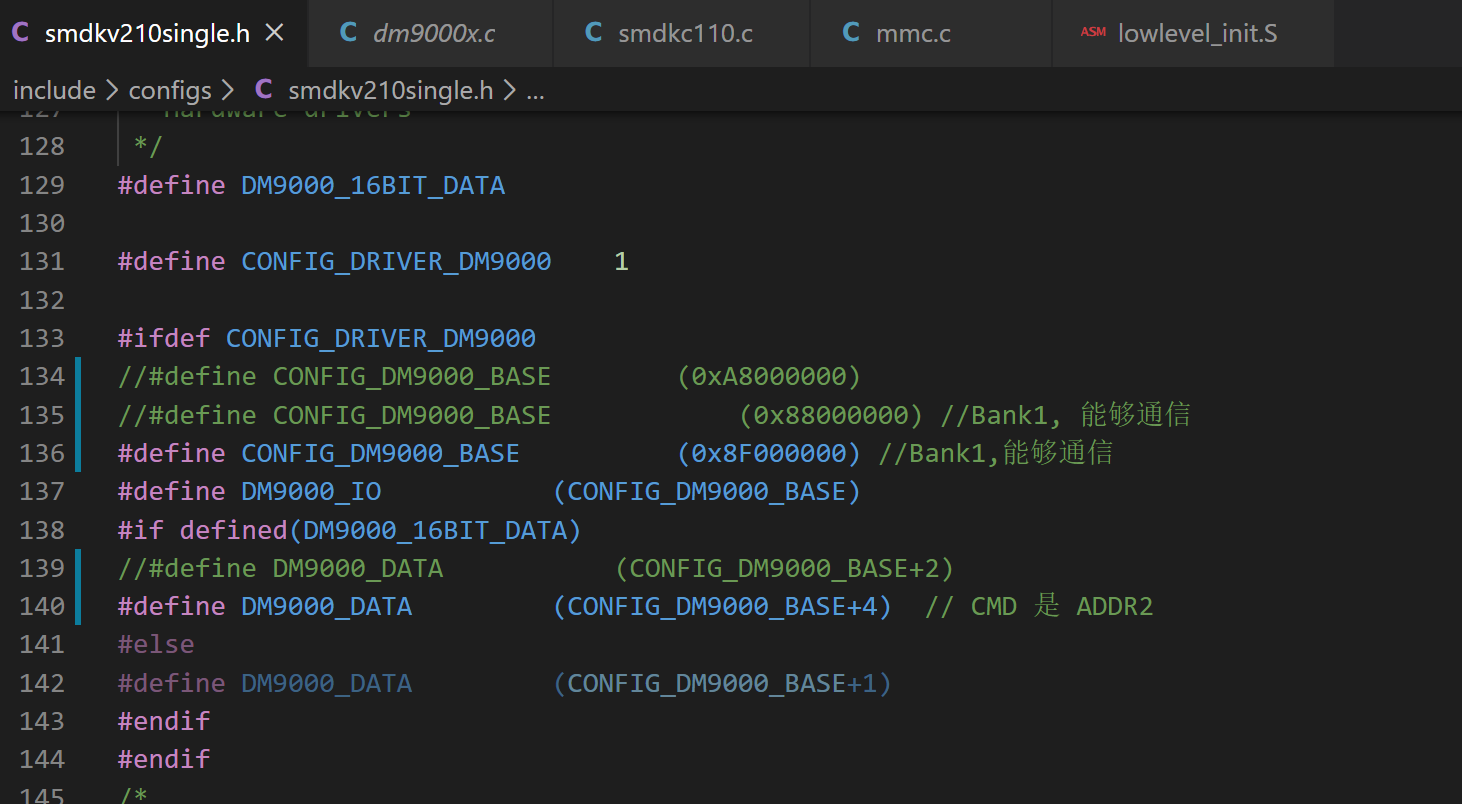
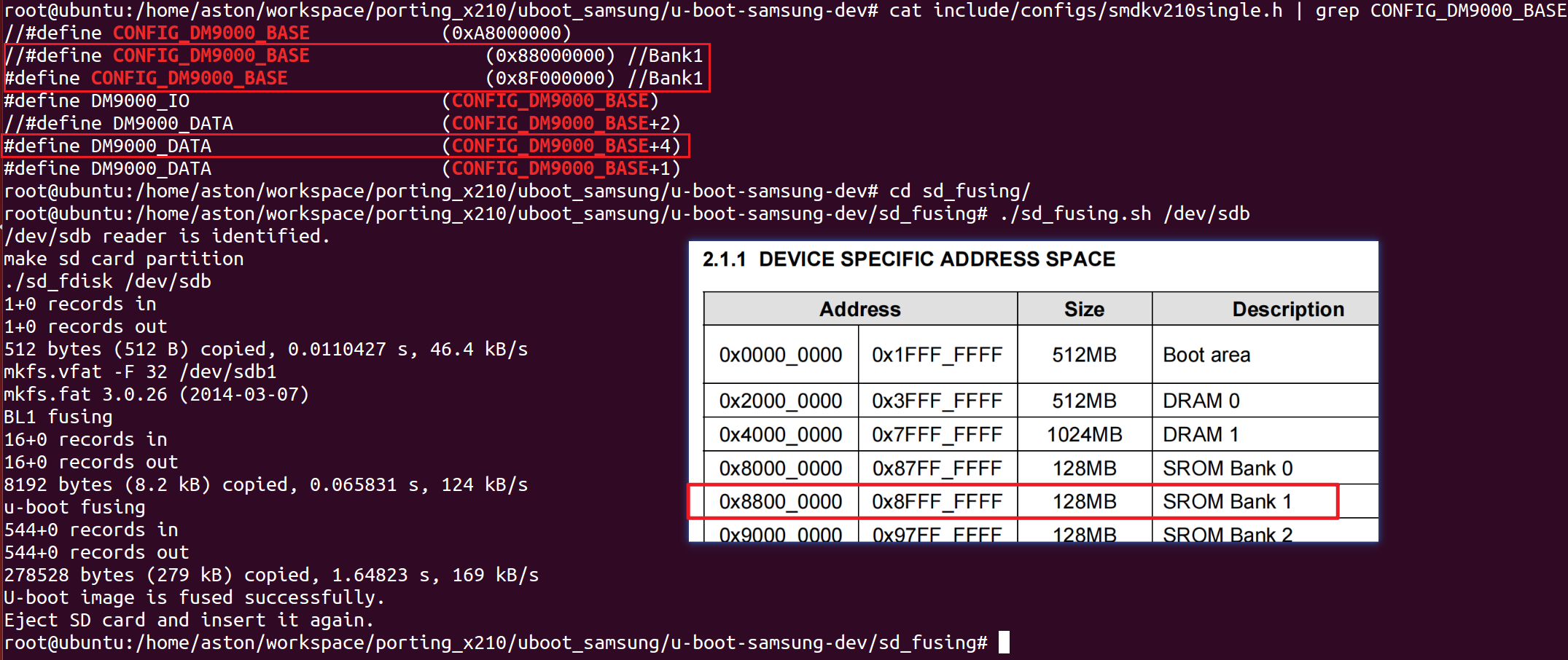
(2) CONFIG_DM9000_BASE 是 DM9000 网卡通过 SROM bank 映射到 SoC 中地址空间中的地址。这个地址的值,取决于硬件接到了哪个 bank,这个 bank 的基地址是 SoC 自己定义好的。譬如我们这里接到了 bank1 上,bank1 的基地址是 0x88000000.
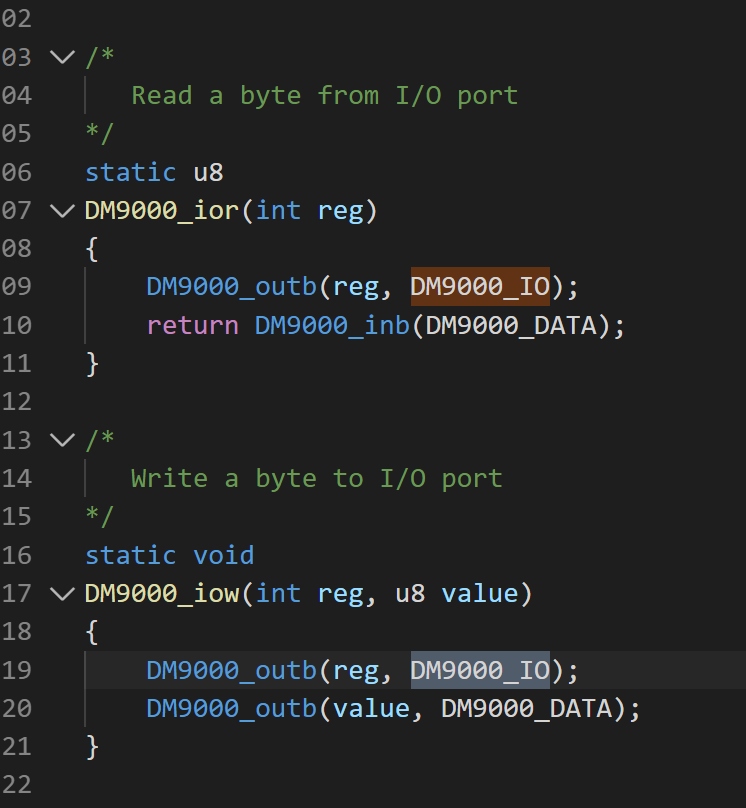
(3) DM9000_IO 表示访问芯片 IO 的基地址,直接就是 CONFIG_DM9000_BASE;DM9000_DATA 表示我们访问数据时的基地址,因为 DM9000 芯片的 CMD 引脚接到了 ADDR2,因此这里要 +4(0b100,对应 ADDR2)。
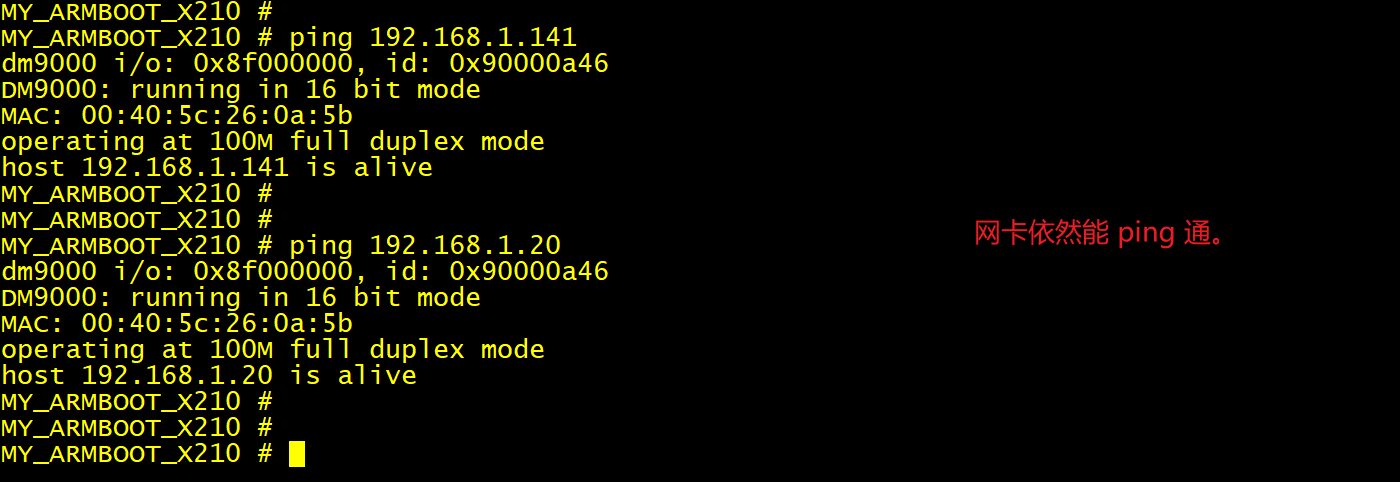
开发板实践,ping 命令成功:
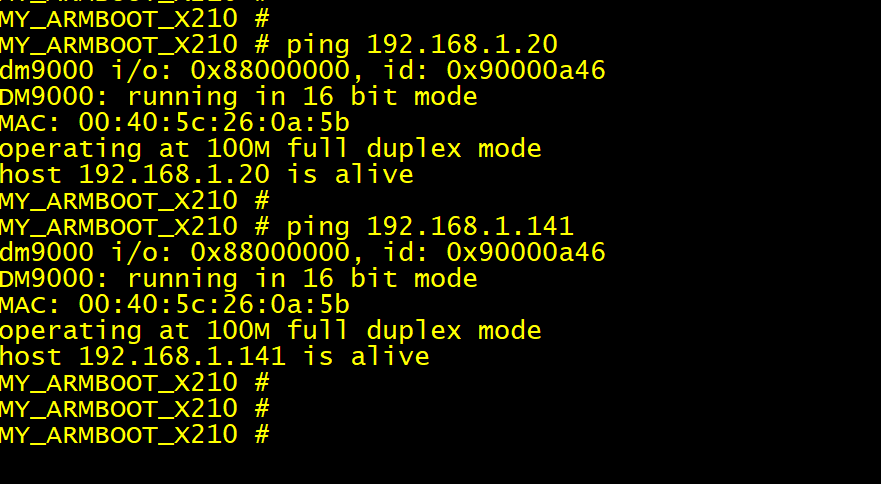
实际上,只要我们的 CONFIG_DM9000_BASE 和 DM9000_DATA 在 SROMC Bank1 的地址范围内,而且区分好 CPU 地址总线的 ADDR2 (第二根地址线)的为 0 和为 1 的两种情况,都是能够正常使用网络通信的。
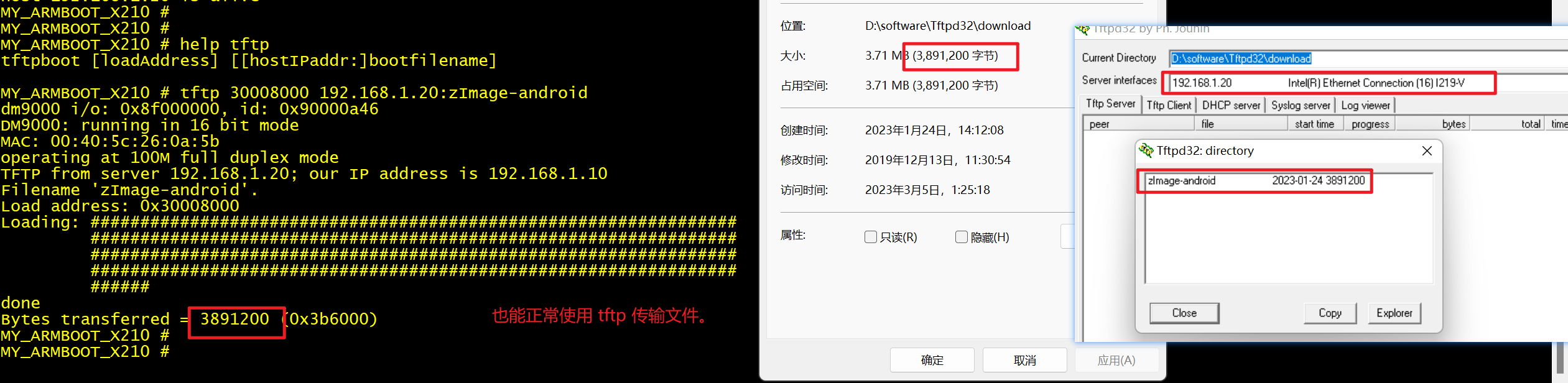
想了解更详细的 DM9000 的信息,可以浏览:链接地址
五、网卡驱动如何工作
1、网卡移植代码实践
(1) 经过实践,网卡驱动移植成功。
(2) 其实还可以做一些实验。譬如说,对网卡驱动初始化部分寄存器的设置,还有网卡 CONFIG_DM9000_BASE 也可以配成 0x88000000 再去试一试。
2、linux 系统中网卡驱动的典型工作方式简介
(1) 在 linux 系统中,网卡算是一个设备,这个设备驱动工作后,会生成一个设备名叫ethn(n 是0、1、2、····)(无线网卡名字一般叫 wlan0、wlan1····)。然后 linux 系统用一些专用命令来操作网卡,譬如 ifconfig 命令。
(2) linux 下的应用程序如何使用网卡驱动来进行网络通信?最通用的方法就是 socket 接口。linux 系统中有一系列的 API 和库函数,提供了一个 socket 编程接口,linux 下的应用程序都是通过 socket 来实现上网的,socket 内部就是间接调用的网卡驱动实现网络通信的。
(3) linux 设计是非常完备的,应用层和驱动层是严格分离的。也就是说,写网络编程应用层的人根本不用管驱动,只要会用 socket 接口即可;写底层驱动的人根本不用管应用层,只要面向 linux 的网络驱动框架模型即可。
3、uboot 中网卡驱动的工作方式简介
(1) 一定要记住:uboot 本身是一个裸机程序,是一个整体,没有分层。所以 uboot 中根本没有驱动和应用的概念。
(2) 按照逻辑来说,ping 这样的命令实现的代码,就是网络应用的应用程序,像dm9000x.c 和 dm9000x.h 这样的代码属于驱动程序。
所以在 uboot 中这些东西是揉在一起的,应用是直接调用驱动实现的。也就是说,ping 命令内部是直接调用了 dm9000 的网卡驱动中的函数来实现自己的。
4、以 ping 命令为例,查找代码验证分析
(1) ping 命令是 uboot 的众多命令之一,ping 命令实现的函数叫 do_ping。
(2) 函数的调用关系:
do_pingNetLoopPingStartPingSendArpRequesteth_send(dm9000x.c中)
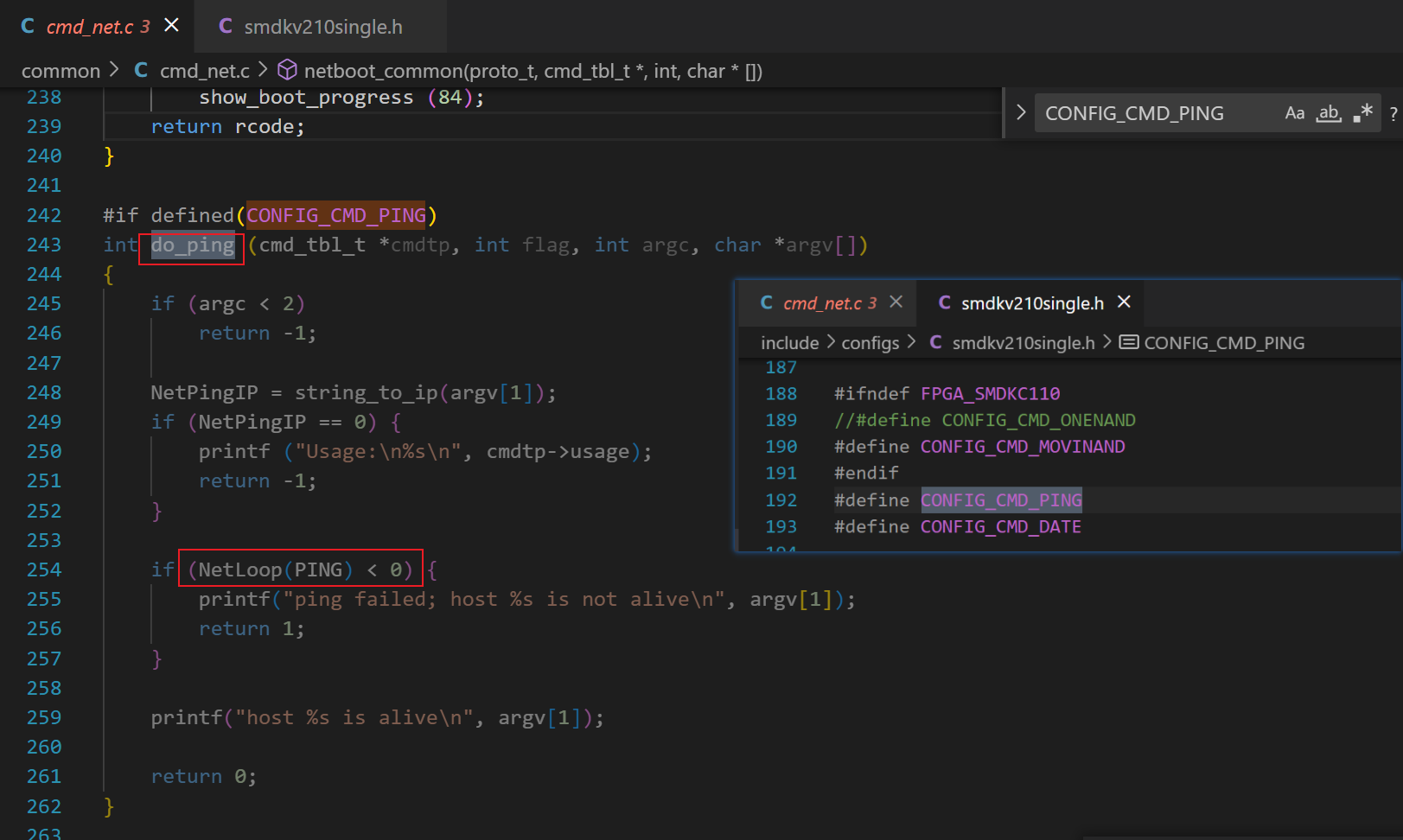
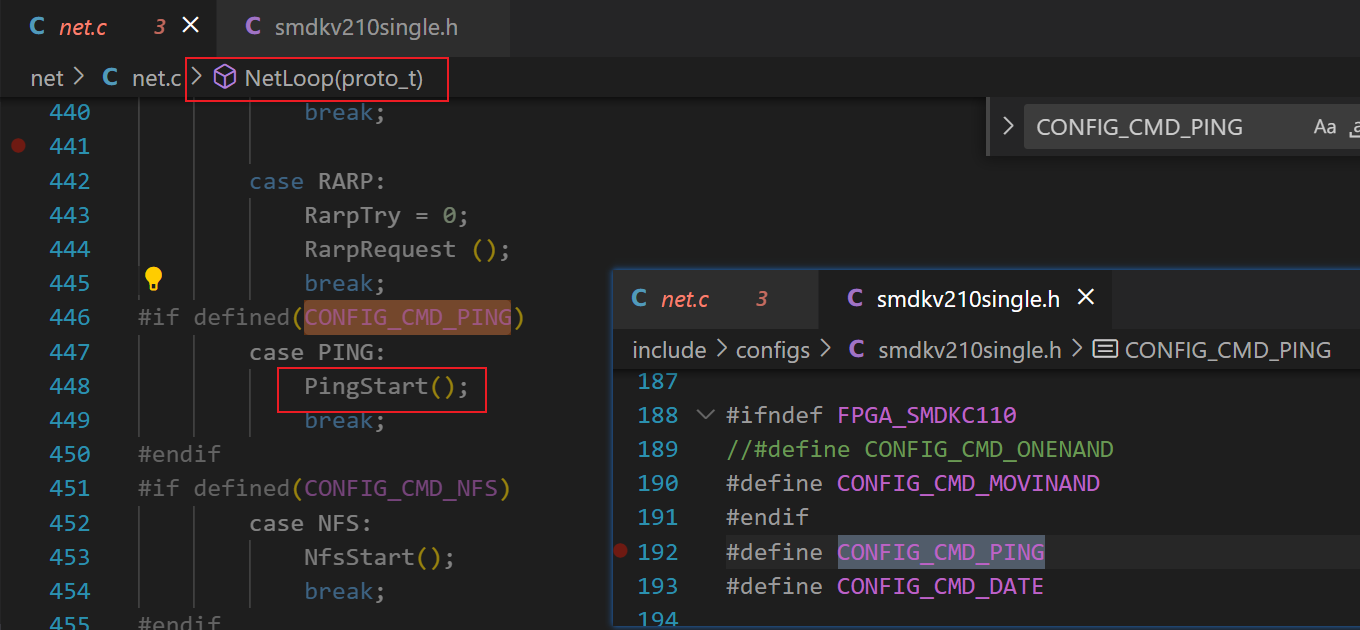
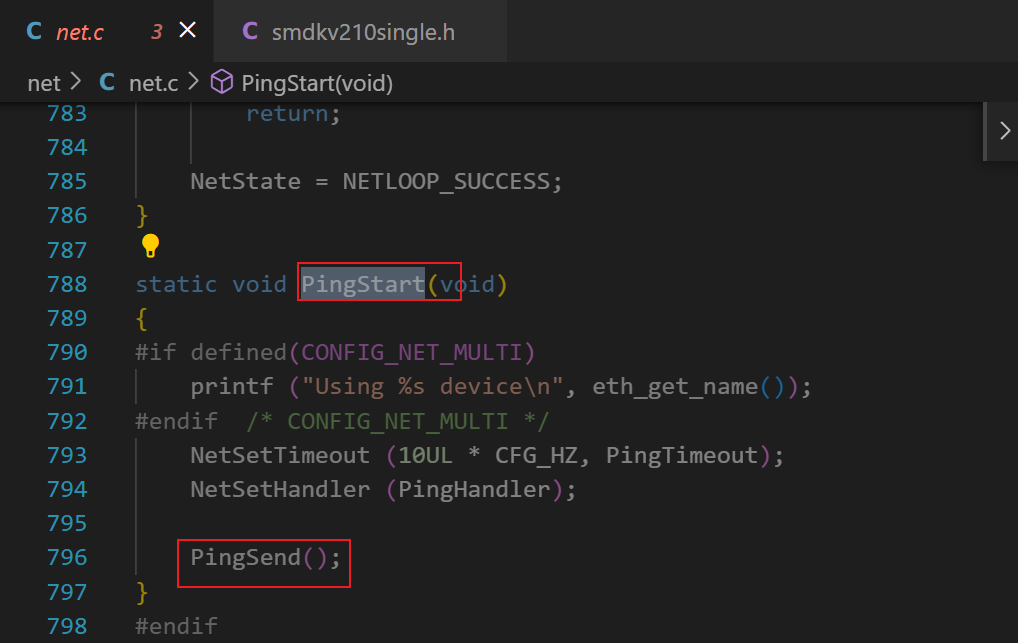
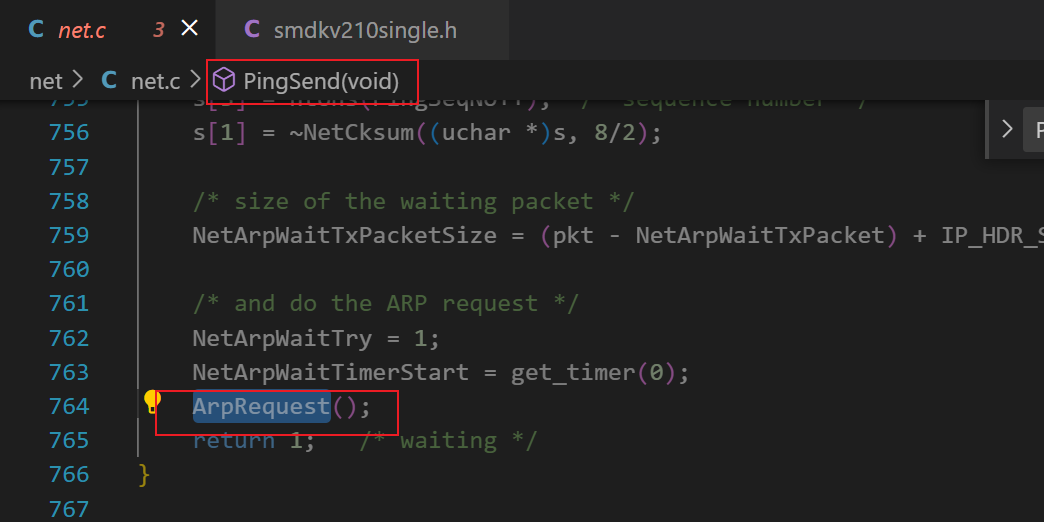
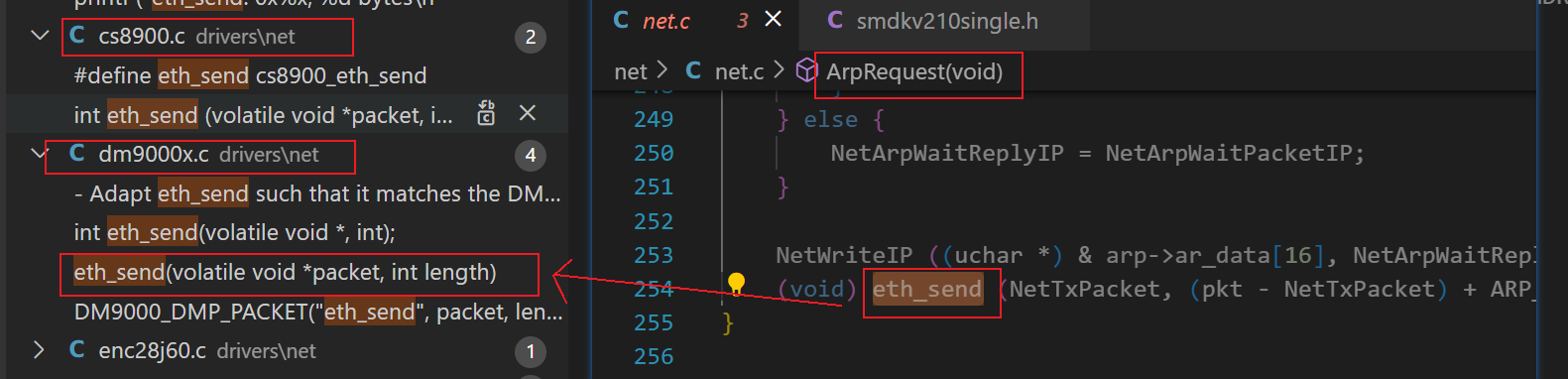
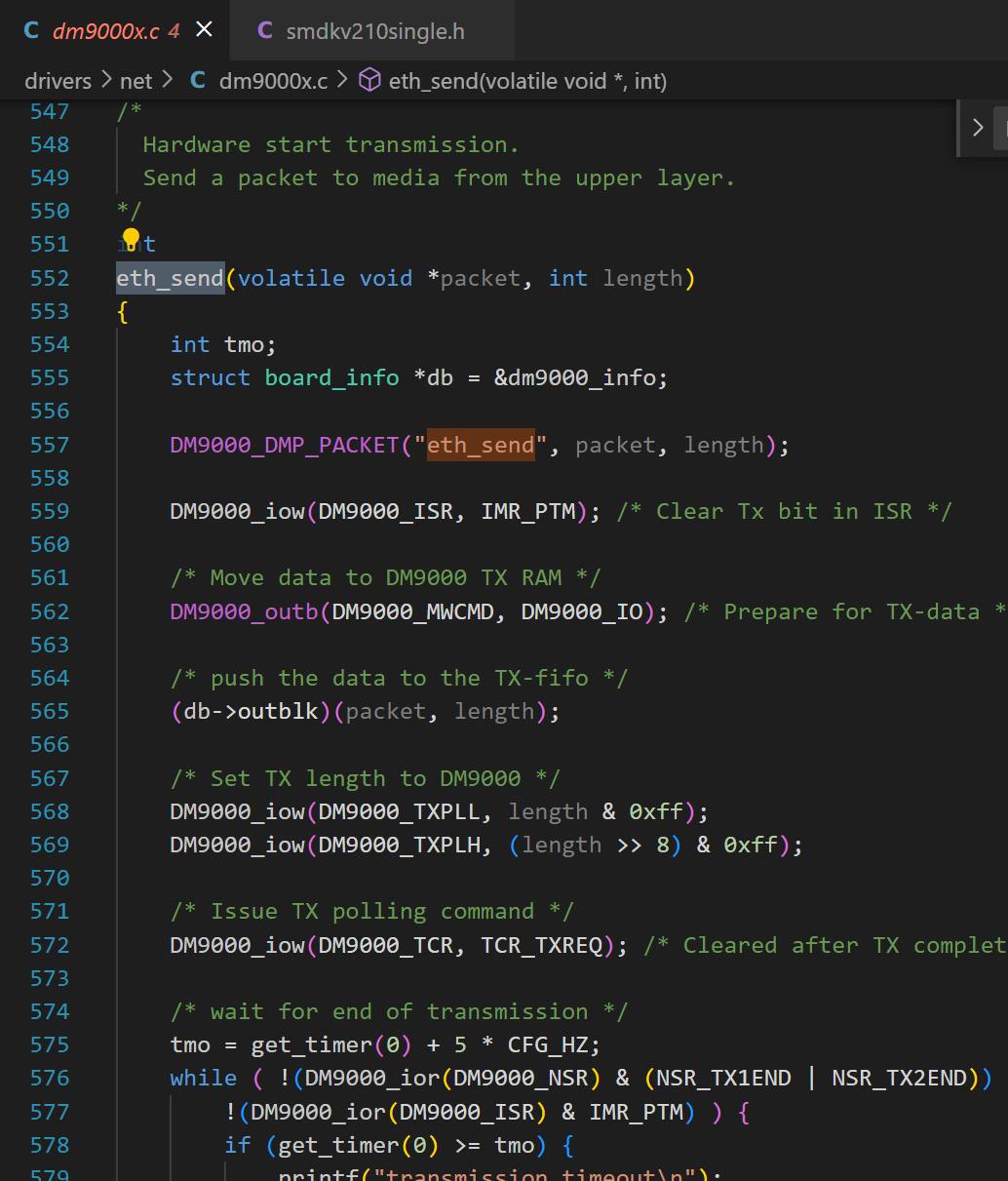
(3) 验证了 《3、uboot 中网卡驱动的工作方式简介》 中说的,uboot 中应用程序(ping)调用驱动程序(dm9000x.c)的方式。这就是一种直接调用的方式。
六、使用自己移植的 uboot 启动内核
1、问题:当前我们移植的 uboot 不能启动内核
(1) 用同样的方法(使用 tftp 0x30008000 zImage-qt; 然后 bootm 0x30008000),分别使用我们自己移植的 uboot, 和使用九鼎移植版本的 uboot, 去启动内核,发现九鼎移植版本的可以启动,但是我们自己移植的不可以启动。到此我们就断定,我们的 uboot 有问题,不能启动内核。
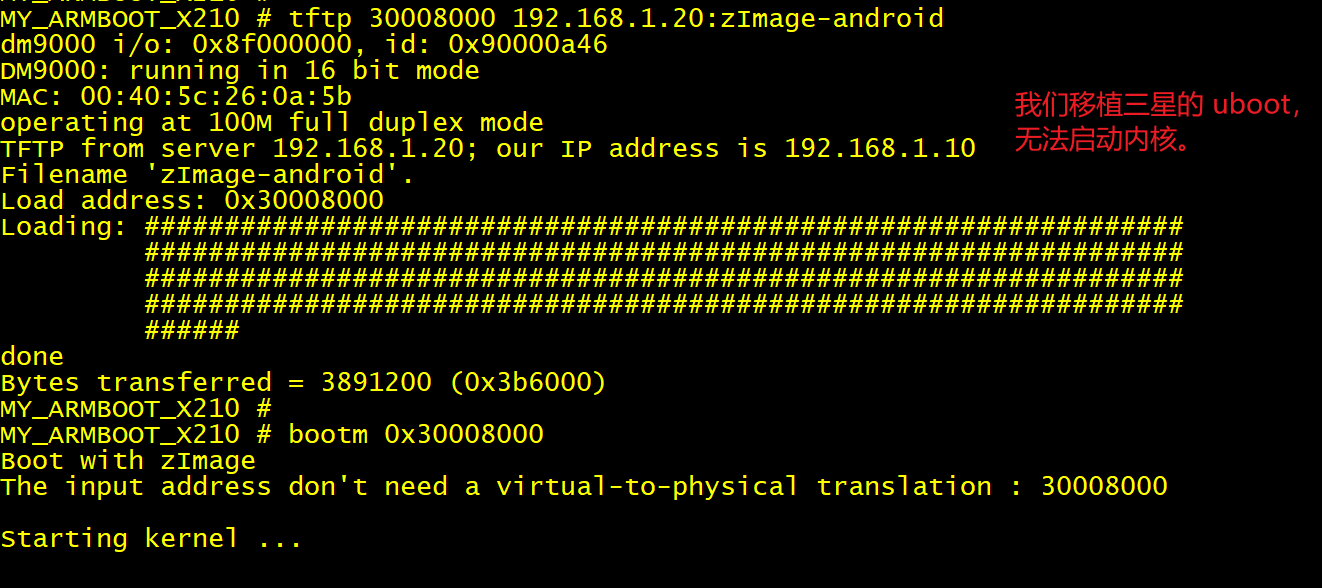
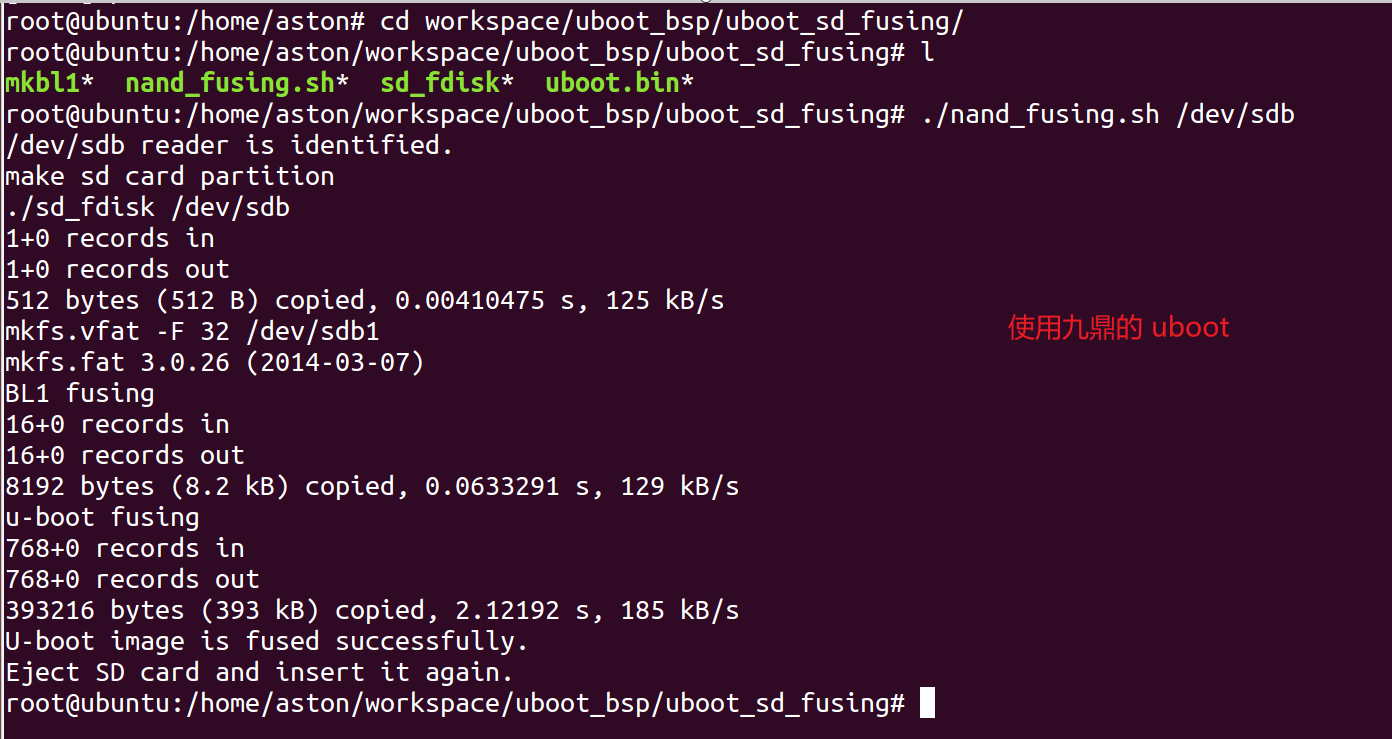
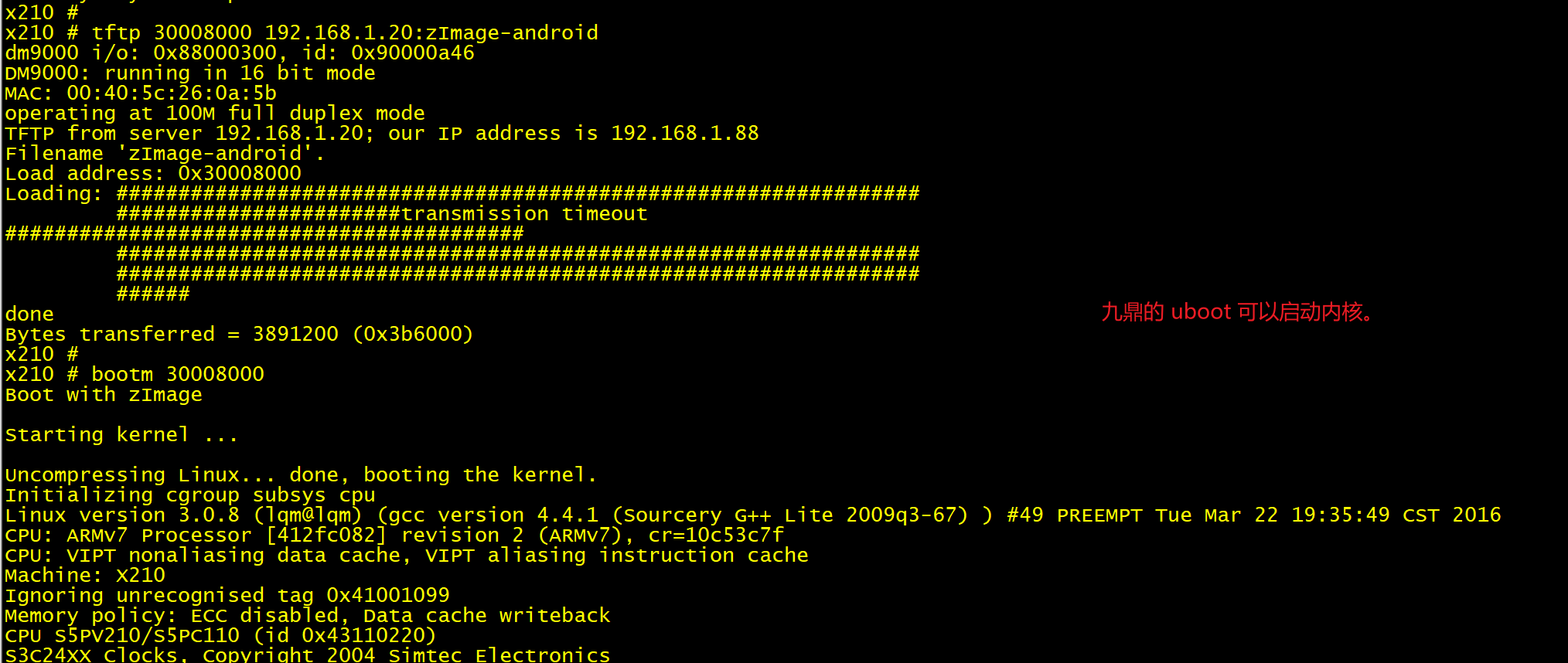
(2) 做基本检查:首先怀疑是机器码不对。经过和九鼎移植版本的 uboot 对比发现,machid 都是 2456,说明机器码没错。

(3) 想到一个问题,我们之前做实验时,将串口改为了串口 0,而内核 zImage-qt 的串口输出在串口 2.怀疑可能的问题是,uboot 使用了串口 0, 而内核使用了串口 2,所以在 uboot 后看不到内核的启动信息。
2、解决第一步:将串口改回串口2
(1) 在 smdkv210single.h 中修改串口编号即可。
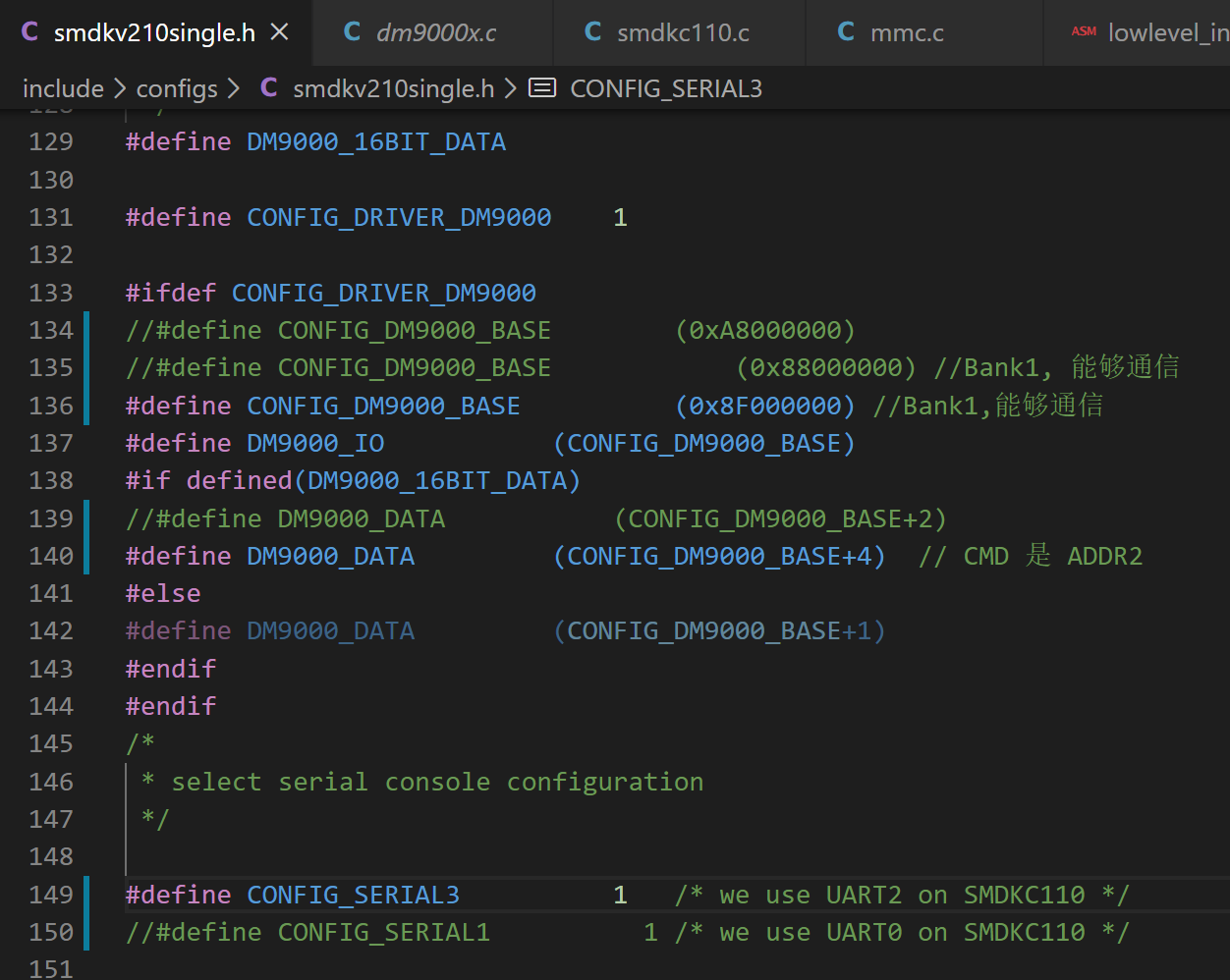
3、根据现象分析,定位问题并试图解决
(1) 如果已经启动了内核,那没什么好说的了。应该是可以直接启动了。
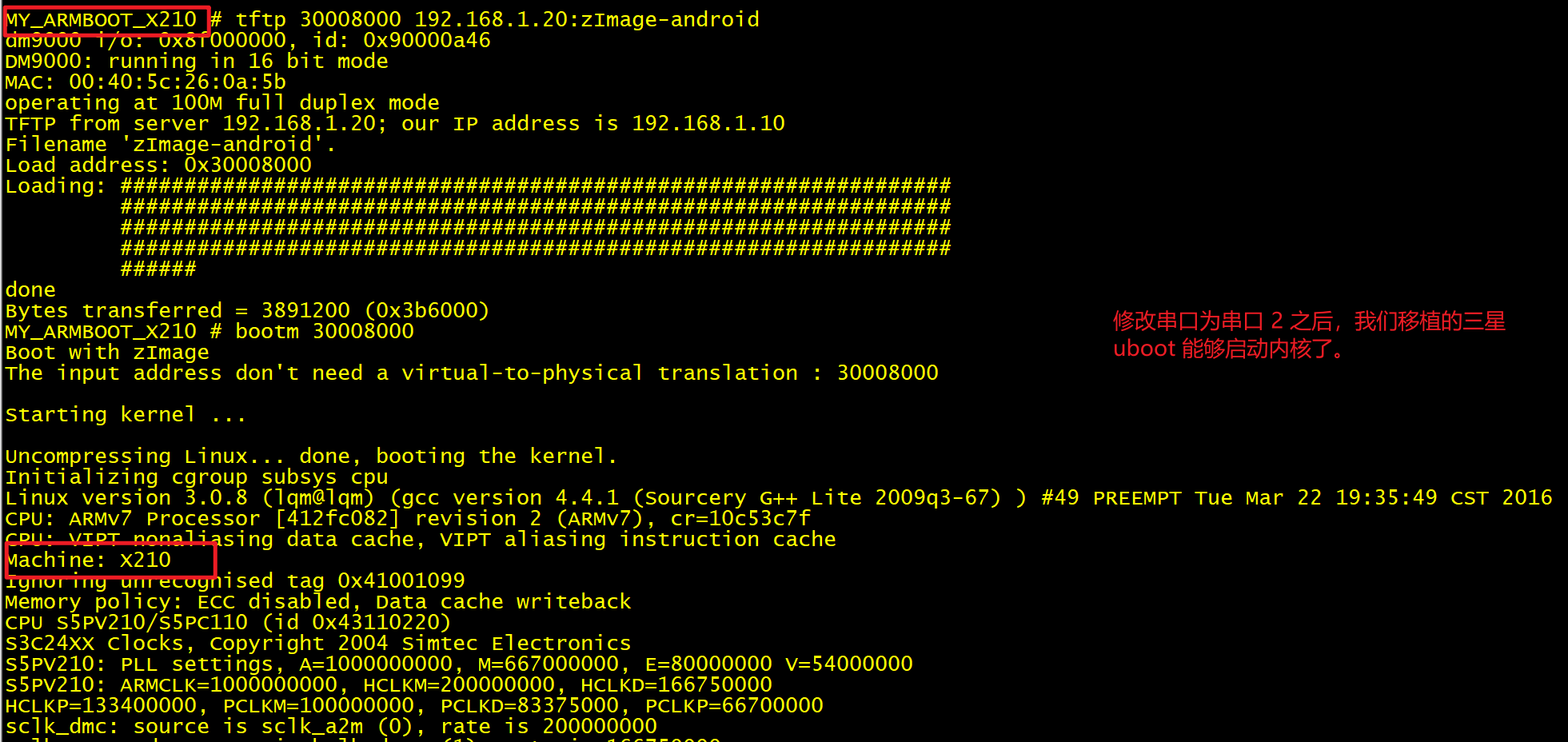
(2) 如何内核没有启动,是 smdkv210single.h 中没有定义 bootm 传参需要的那几个宏造成的。
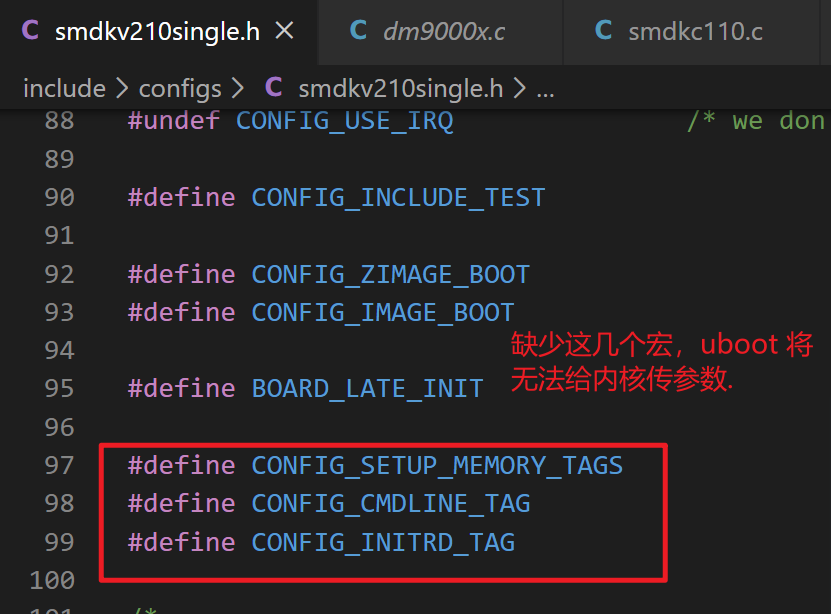
源自朱友鹏老师.
