优化网站排名如何有赞商城官网登录
一、VMware Workstation16安装
选择安装VMware Workstation,登录其官网下载安装包,链接如下:
下载 VMware Workstation Pro
下载后运行安装向导,一直Next即可。
二、Ubuntu镜像下载
ubuntu20.04
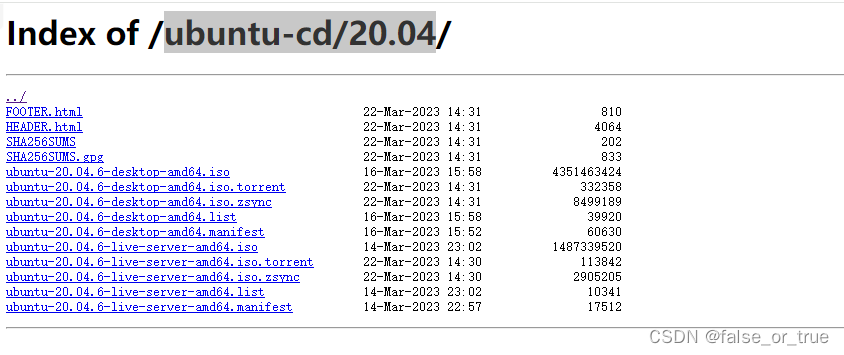
选择需要下载的镜像类型下载即可
三、新建虚拟机
- 打开第一步所下载的VMware Workstation。在主界面中,选择【创建新的虚拟机】。
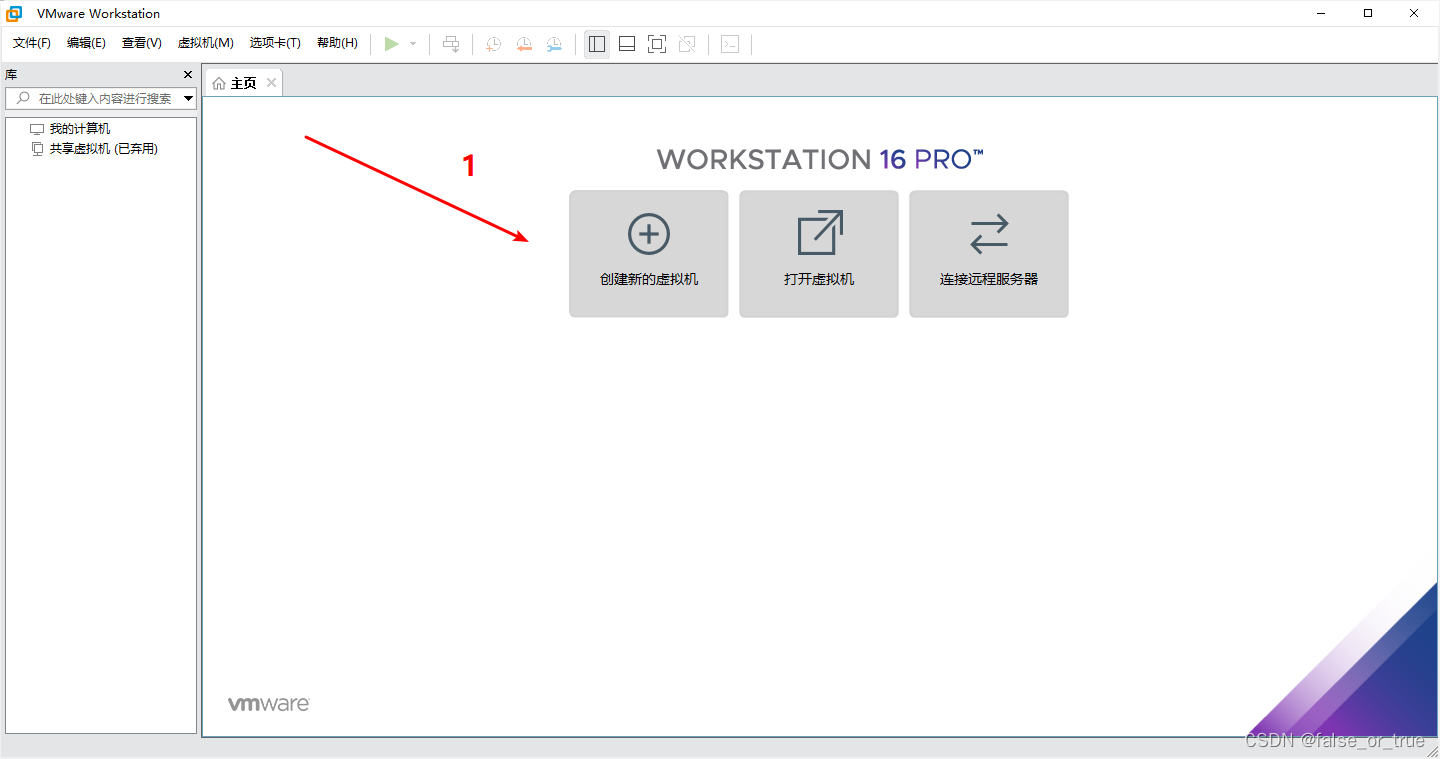
- 如图,会自动弹出【新建虚拟向导】,选择【自定义(高级)】后,点击【下一步】。
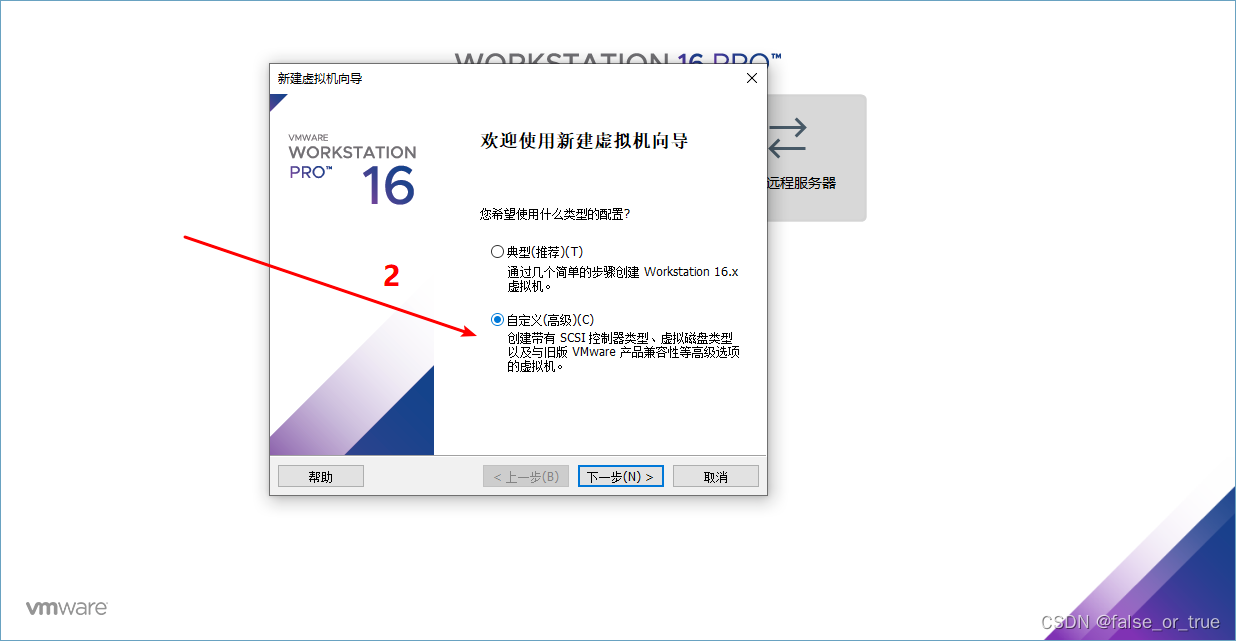
这一步选择默认值即可,点击【下一步】。
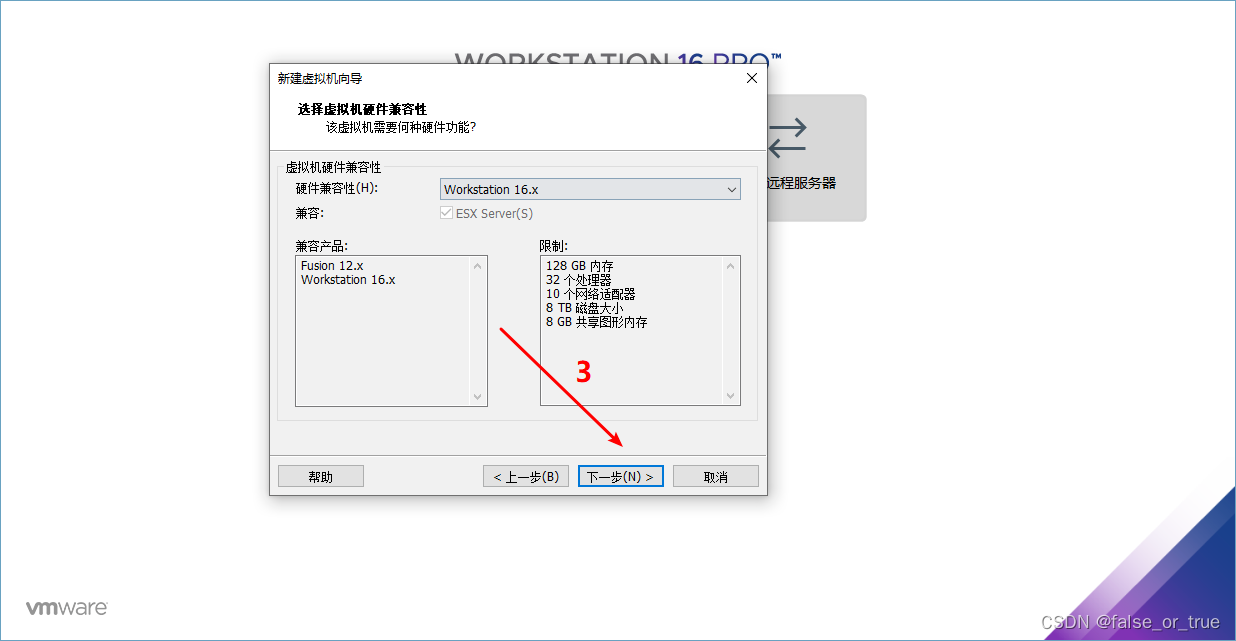
选择【稍后安装操作系统】,点击【下一步】

选择【Linux】,其下方版本将默认更改为【Ubuntu】。
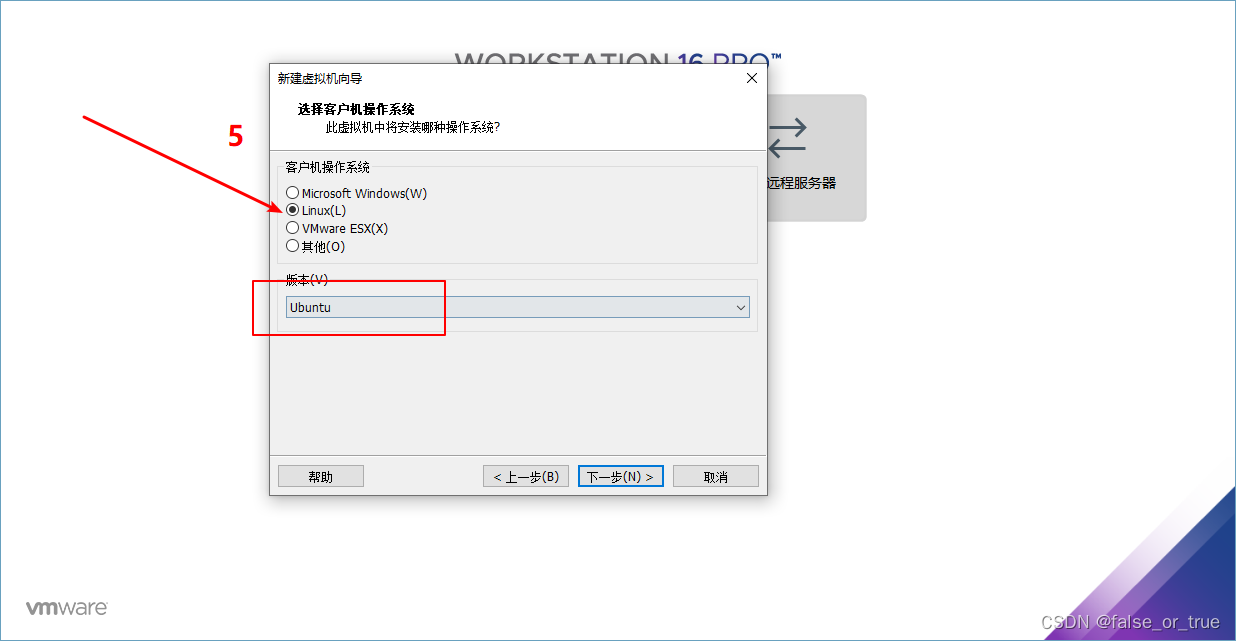
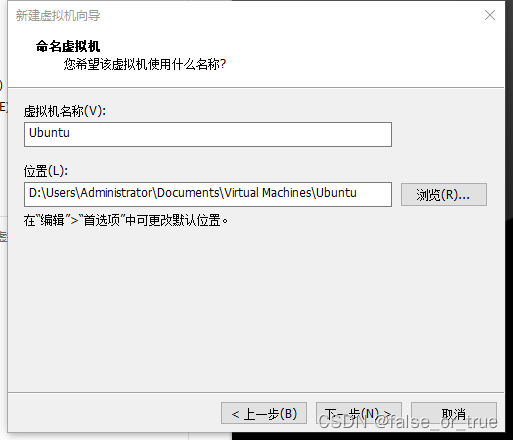
填写【虚拟机名称】及【位置】,点击【下一步】。【虚拟机名称】即虚拟机的名字。【位置】可以选择容量较大的硬盘位置。
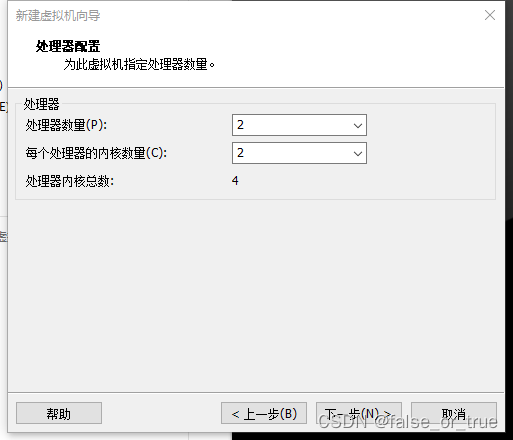
【处理器数量】与【每个处理器的内核数量】选择2后,点击【下一步】。
选择【此虚拟机的内存】,此值应依据电脑本身情况酌情调整。常用值为1G(1024MB)、2G(2048MB)、4G(4096MB)等等。在这里选择2G。
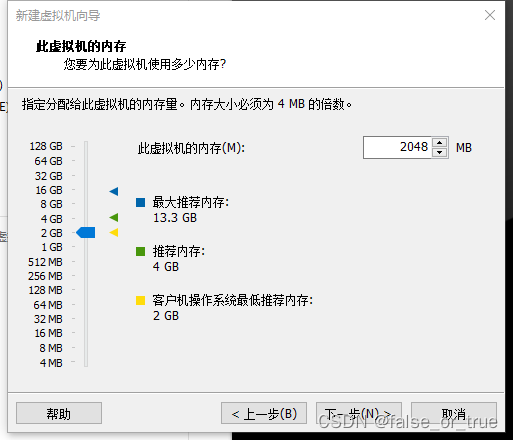
选择【使用网络地址转换】,点击【下一步】。
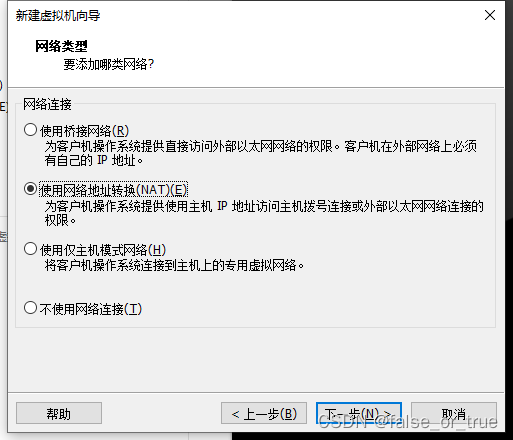
选择推荐的I/O控制器类型即可,点击【下一步】。
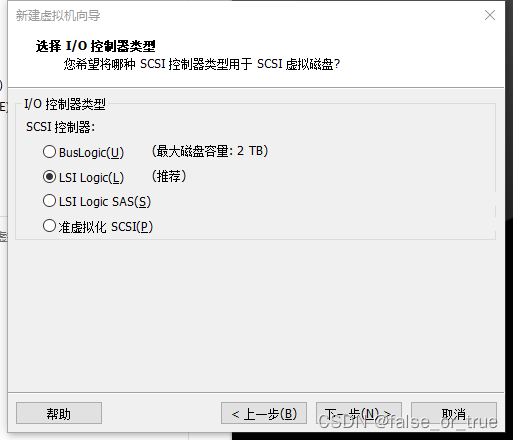
选择推荐的磁盘类型即可,点击【下一步】。
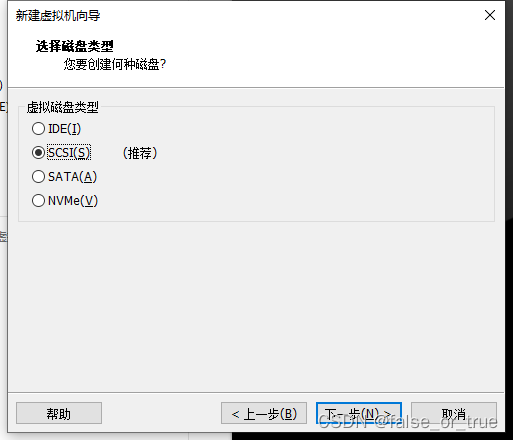
选择【创建新虚拟磁盘】,点击【下一步】。
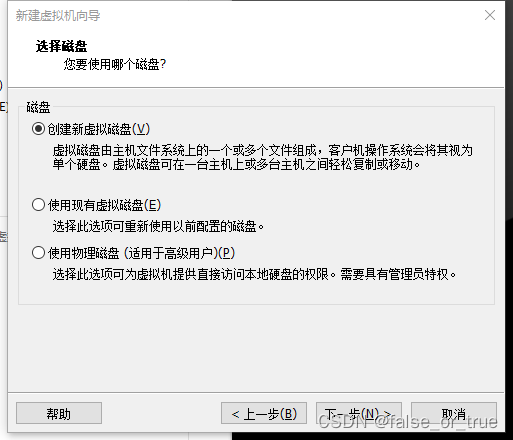
设置【最大磁盘大小】为40,并选择【将虚拟磁盘拆分成多个文件】后,点击【下一步】。最大磁盘大小默认为20GB,磁盘剩余空间较大的话该数值可以往上加。
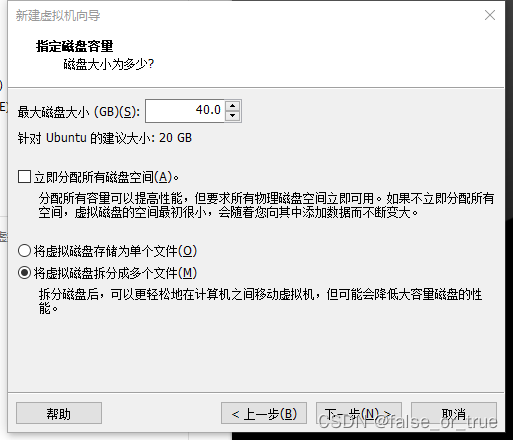
点击【下一步】。

点击【完成】。
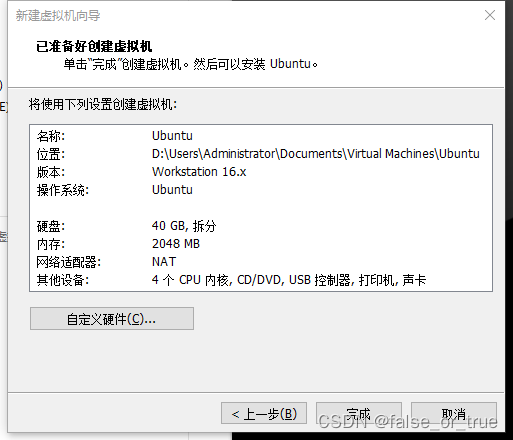
四、挂载镜像
回到VMware界面,单机界面左侧【编辑虚拟机位置】。
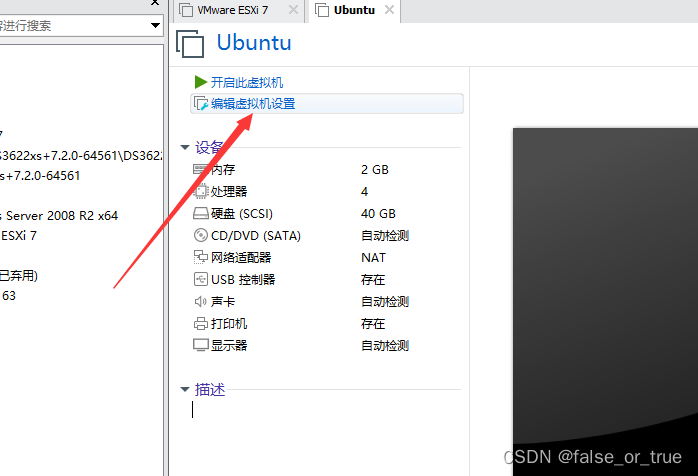
点击左侧的CD/DVD选项卡,右侧点击【使用ISO映像文件】,找到第二步在你清镜像中下载的Ubuntu镜像即可,点击【下一步】。
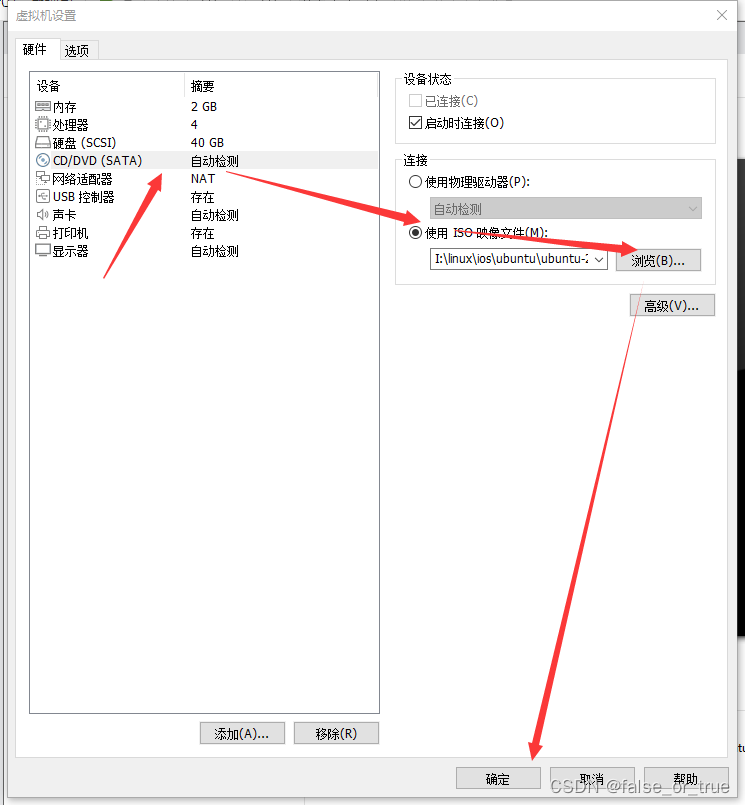
确保启动时连接打钩
五、安装系统
回到VMware界面,点击【开启此虚拟机】。
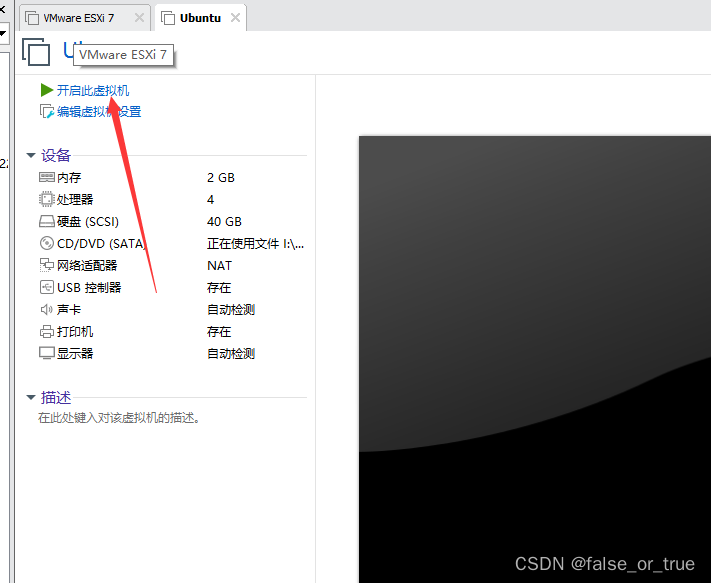
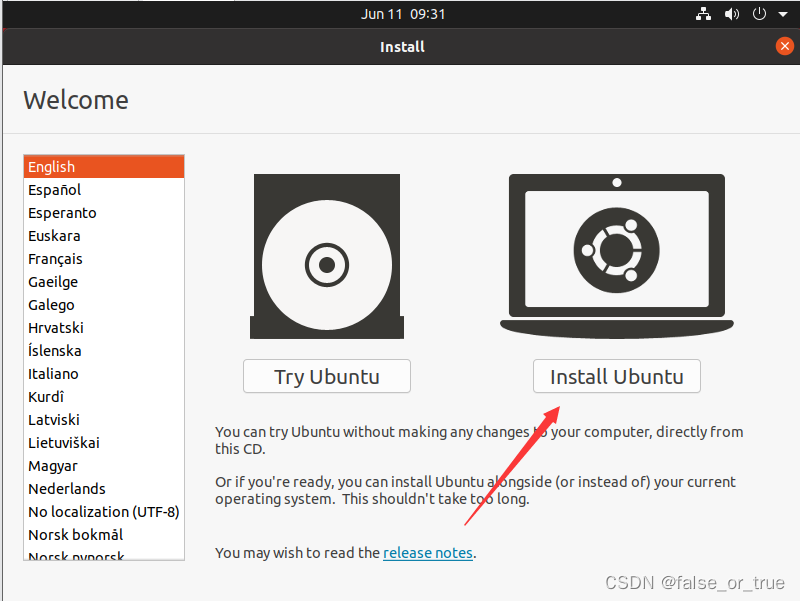
此时可以看到虚拟机画面,点击右侧【Install Ubuntu】。
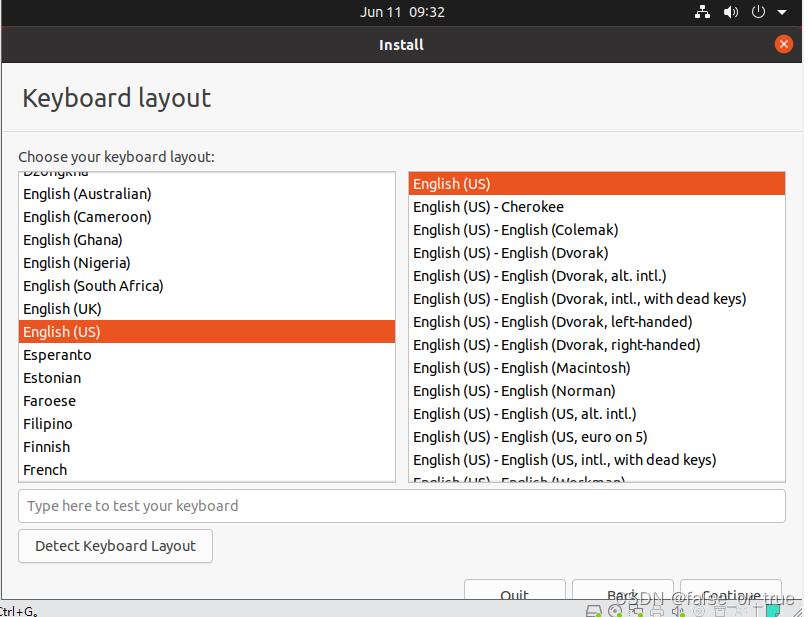
此时我们使用美国键盘布局【English(US)】,点击【Continue】。
点击【Minimal installation】,点击【Continue】。由于Ubuntu虚拟机大多做学习研发使用,所以选择最小化安装。若是有用Ubuntu网上冲浪和打游戏的需求,请选择【Normal installation】。

选择【Erase disk and install Ubuntu】,点击【Install Now】。
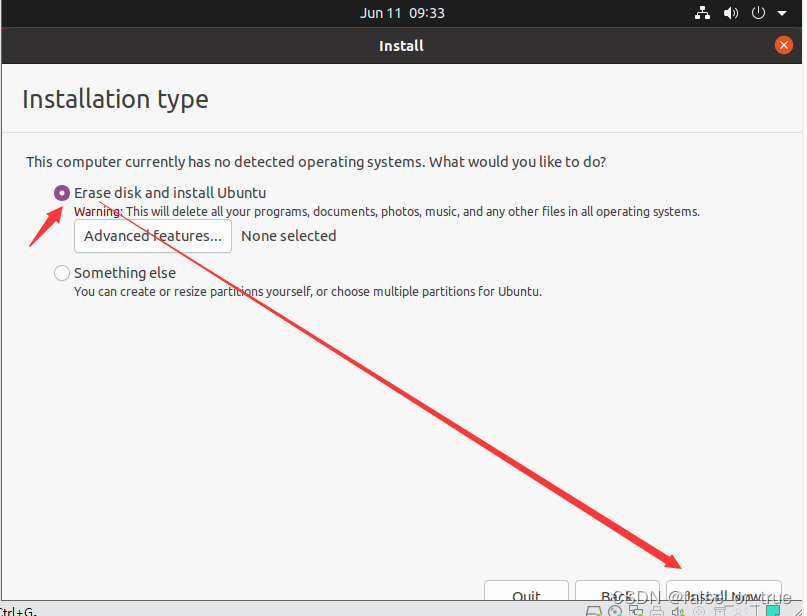
点击【Continue】确认。
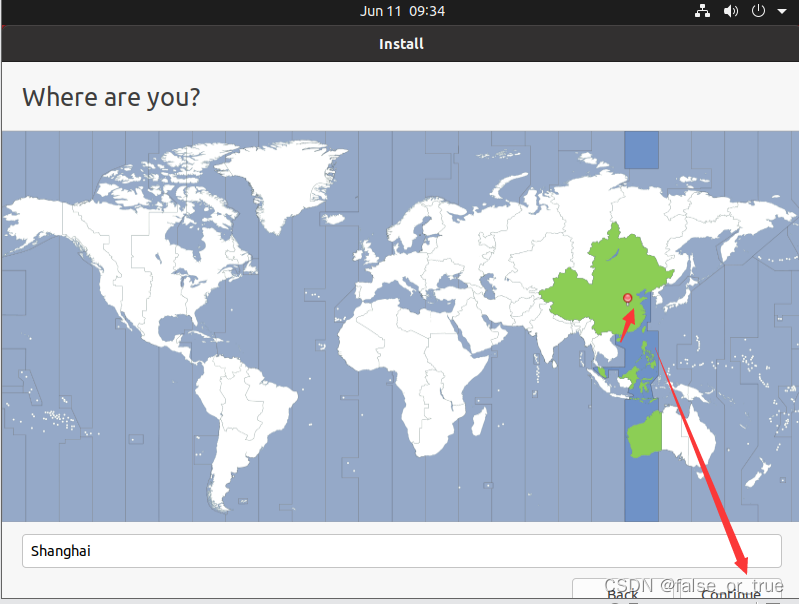
点击地图上【中国】的位置,会默认出现Shanghai,点击【Continue】。
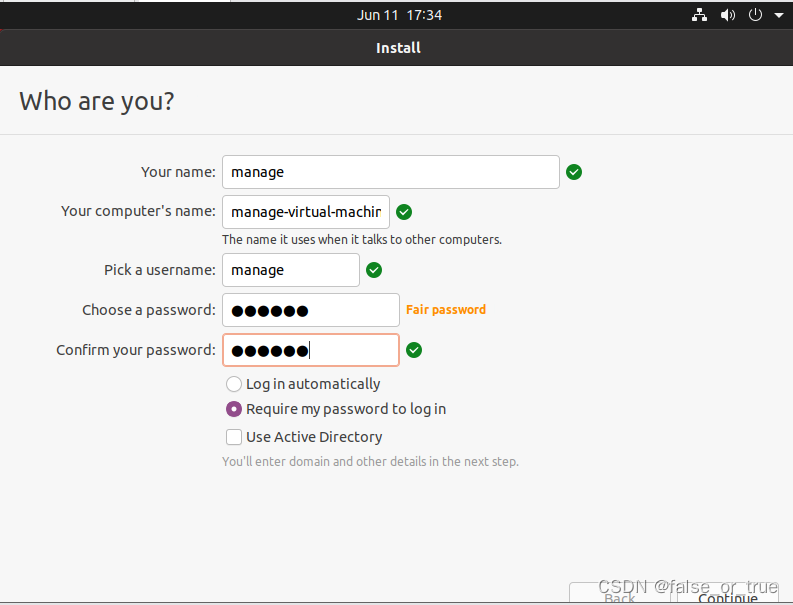
输入【Your name】【Your computer’s name】【Pick a username】【Choose a password】【Confirm your password】后,点击【Continue】。这里建议密码设置的简单一些,因为Ubuntu后续很多操作需要验证密码,设置复杂的密码后期会比较麻烦。
等待安装。
点击【Restart Now】重新启动。
重新启动后,可以看到Ubuntu已经安装完成。
