当前位置： 首页 > news >正文

网站建设宀金手指花总十五做我的世界皮肤壁纸的网站

news 2025/11/2 22:15:16
网站建设宀金手指花总十五,做我的世界皮肤壁纸的网站,wordpress多级菜单,wordpress禁止谷歌字体🐵本篇文章将对数据结构中7大排序的知识进行讲解 一、插入排序 有一组待排序的数据array，以升序为例，从第二个数据开始（用tmp表示）依次遍历整组数据，每遍历到一个数据都再从tmp的前一个数据开始&#xff0…

🐵本篇文章将对数据结构中7大排序的知识进行讲解

一、插入排序

有一组待排序的数据array，以升序为例，从第二个数据开始（用tmp表示）依次遍历整组数据，每遍历到一个数据都再从tmp的前一个数据开始（下标用j表示）从后往前依次和其进行比较，如果tmp比它小，则令array[j + 1] = array[j];

1.1 实例讲解

第一趟：

第二趟：

第三趟和第四躺：

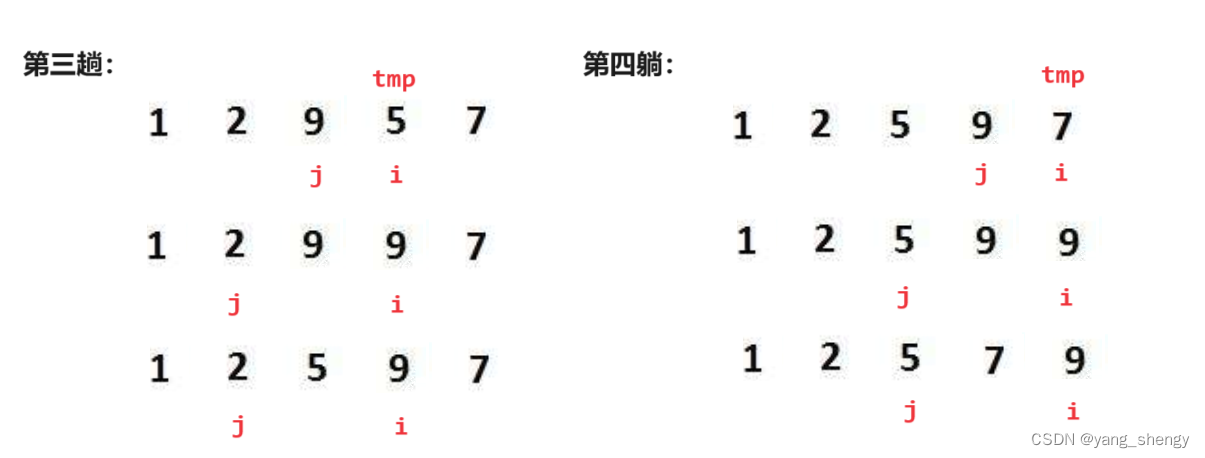
1.2 代码实现

    public void insertSort(int[] array) {for (int i = 1; i < array.length; i++) {int tmp = array[i];int j = i - 1;for (; j >= 0; j--) {if (tmp < array[j]) {array[j + 1] = array[j]; //将tmp移动到当前数据顺序的最小位置处，此步操作相当于给tmp腾位置} else {break;}}array[j + 1] = tmp;}}

在该排序算法中，当tmp前面出现比其小的元素时，则再往前的数据也一定比tmp小，所以插入排序是元素越有序，其效率越快的排序算法

时间复杂度：O(N²)

空间复杂度：O(1)

稳定

二、希尔排序

希尔排序是对直接插入排序的优化，它会将一组数据进行分组，然后针对每一组进行直接插入排序，那么该如何进行分组：定义一个gap，代表同一组数据的间隔，比如由一组数据：6，5，4，3，2，1；gap = 2，则6，4，2为一组，5，3，1为一组。在gap = 2的情况下的每一组数据排序完毕后，要缩小gap并再进行分组，然后再对每一组进行插入排序，随着gap的减小，该组数据会变得越来越有序，当gap = 1时，此时数据已经接近有序了，所以效率会非常快 

2.1 实例讲解

第一躺：

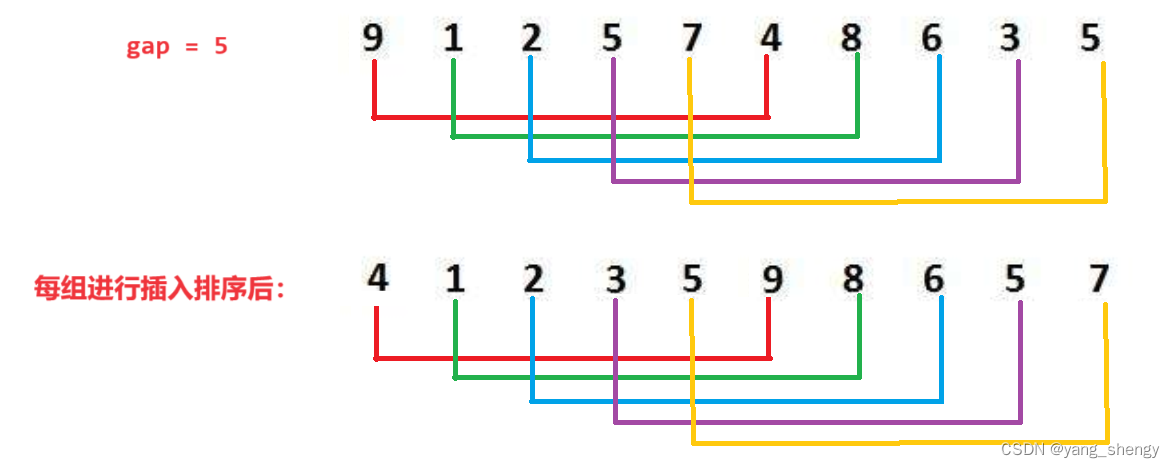
第二趟：

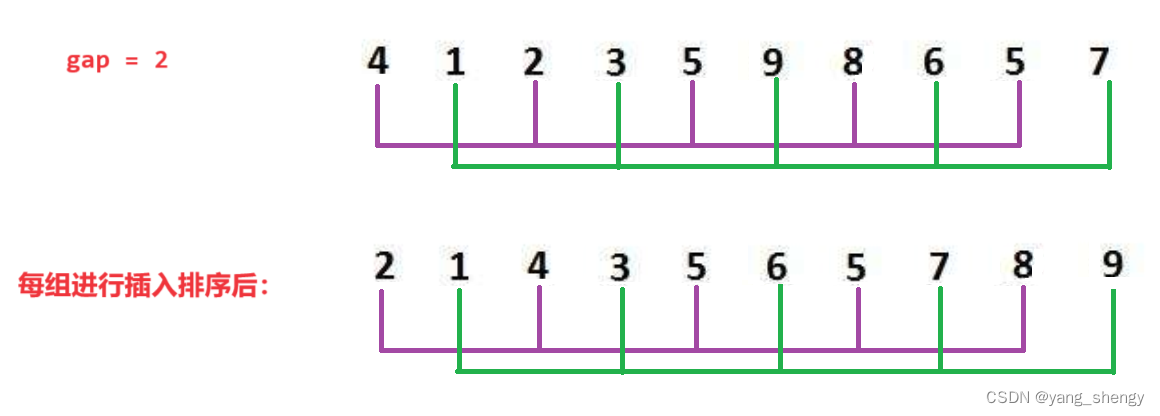
第三趟：

2.2 代码实现

    public void shellSort(int[] array) {int gap = array.length;while(gap > 1) { //当gap = 1时分组结束gap = gap / 2;shell(array, gap);}}private void shell(int[] array, int gap) {for (int i = gap; i < array.length; i++) {int tmp = array[i];int j = i - gap;for (; j >= 0; j -= gap) {if (tmp < array[j]) {array[j + gap] = array[j];} else {break;}}array[j + gap] = tmp;}}

希尔排序不稳定

三、选择排序

选择排序较为简单，这里直接讲实例

3.1 实例讲解

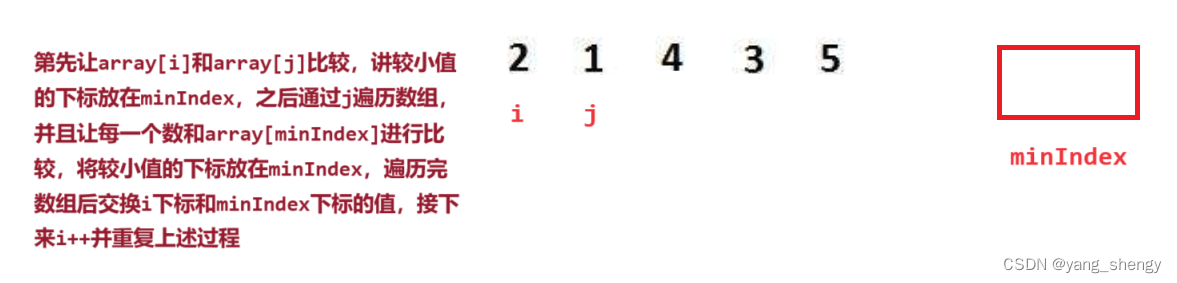
第一躺：

第二趟：

第三趟：

第四躺和第五躺也都是如此排序的，由于数据已经有序，这里就不再演示

3.2 代码实现

    public void selectSort(int[] array) {for (int i = 0; i < array.length; i++) {int minIndex = i;int j = i + 1;for (; j < array.length; j++) {if (array[j] < array[minIndex]) {minIndex = j;}}swap(array, minIndex, i);}}private void swap(int[] array, int minIndex, int i) {int tmp = array[minIndex];array[minIndex] = array[i];array[i] = array[minIndex];}

选择排序的效率不是很高，日常开发使用较少

时间复杂度：O(N²)

空间复杂度：O(1)

不稳定

四、堆排序

在上篇文章：Java优先级队列（堆）中进行了讲解，这里只给出代码：

4.1 代码实现

    public void createHeap(int[] array) { //创建大根堆int usedSize = array.length;for (int parent = (usedSize - 1 - 1) / 2; parent >= 0; parent--) {siftDown(array, parent, usedSize);}}private void siftDown(int[] array, int parent, int end) { //向下调整int child = 2 * parent + 1;while(child < end) {if (child + 1 < end && array[child] < array[child + 1]) {child++;}if (array[parent] < array[child]) {swap(array, parent, child);parent = child;child = 2 * parent + 1;} else {break;}}}private void swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}public void heapSort(int[] array) { //堆排序createHeap(array);int end = array.length - 1;while(end > 0) {swap(array, 0, end);siftDown(array, 0, end - 1);end--;}}

堆排序：

时间复杂度：O(N * logN)

空间复杂度：O(1)

不稳定

五、冒泡排序

冒泡排序在C语言阶段也进行了详细讲解，这里也只给出代码：

5.1 代码实现

    public void bubbleSort(int[] array) {for (int i = array.length - 1; i > 0; i--) {for (int j = 0; j < i; j++) {if (array[j] > array[j + 1]) {int tmp = array[j];array[j] = array[j + 1];array[j + 1] = tmp;}}}}

冒泡排序

时间复杂度：O(N²)

空间复杂度：O(1)

稳定

六、快速排序

6.1 实例讲解

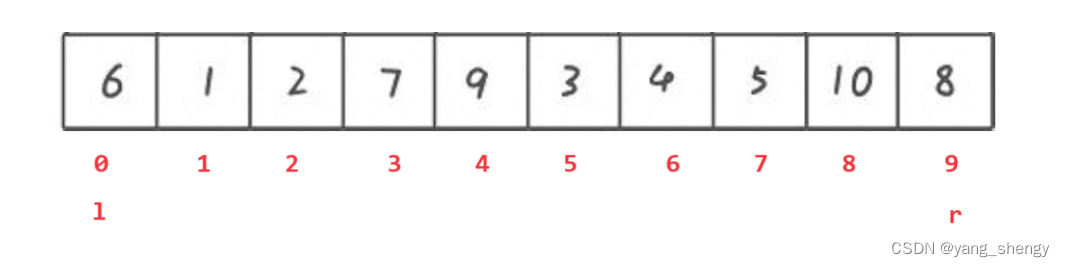
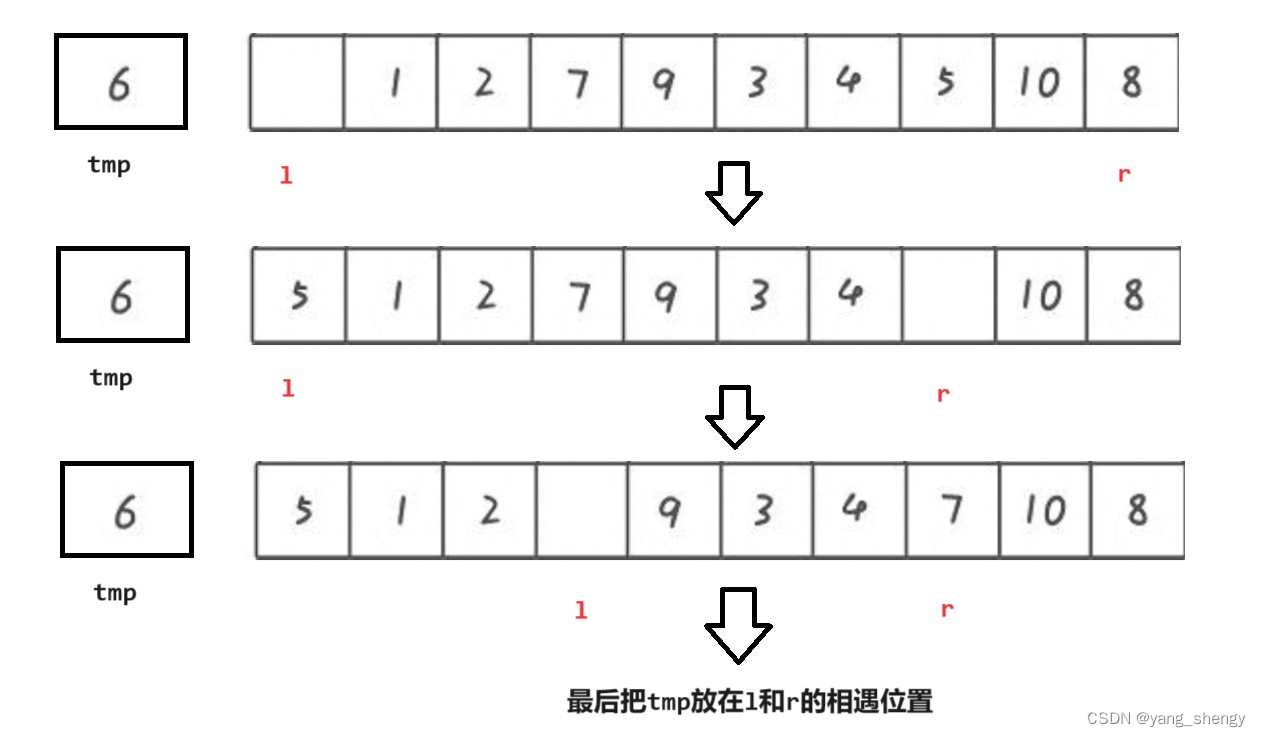
以最左边的数作为基准，先从数组的最右边开始遍历，当找到比基准小的数时停止，然后从数组的最左边开始遍历，当找到比基准大的数时停止，这时将 l 和 r 所对应的值进行交换，之后重复上述过程直到 left 和 right 相遇，相遇的下标定义为pivot，最后将pivot下标的值和tmp进行交换

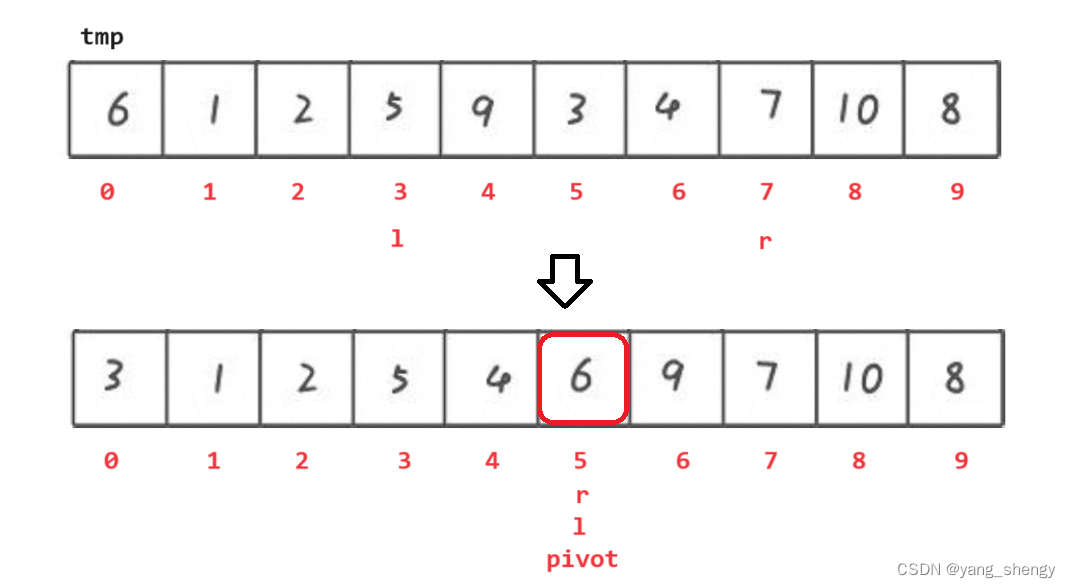
此时6的左边都是比其小的数，6的右边都是比其大的数；之后分别对6左边的数据和右边的数据进行重复的操作

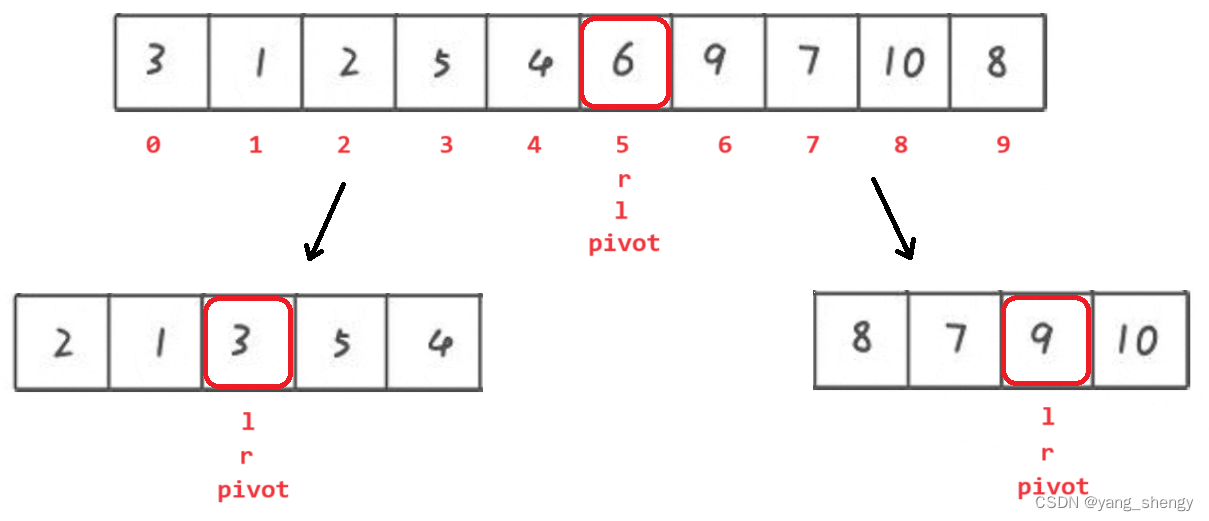
之后再对这两组数据的pivot的两边进行重复操作，由此可以联想到使用递归，类似于二叉树

6.2 代码实现

    public void quickSort(int[] array) {quick(array, 0, array.length - 1);}private void quick(int[] array, int start, int end) {int pivot = partition(array, start, end); //通过paratition方法得到 left 和 right 相遇的下标 （paratition后续再实现）quick(array, start, pivot - 1); //递归 pivot 的左边quick(array, pivot + 1, end); //递归 pivot 的右边}

上述的 quick 方法中还缺少递归结束的条件，第一种不难想到就是left 和 right相遇时

第二种情况如下图：

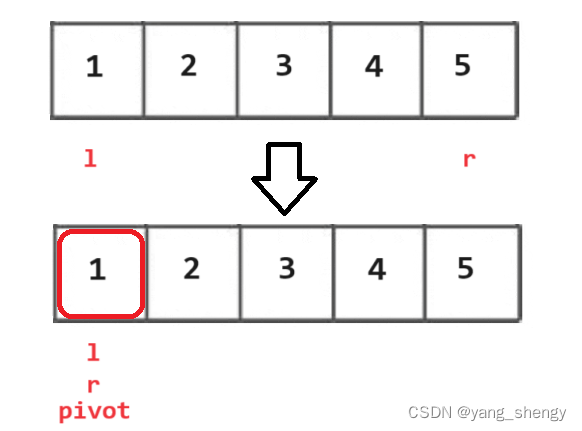
上图的下一步是r = pivot - 1；开始递归pivot的左边，但其左边并没有数据，所以当left > right时结束递归

    public void quickSort(int[] array) {quick(array, 0, array.length - 1);}private void quick(int[] array, int start, int end) {if (start >= end) {return;}int pivot = partition1(array, start, end);quick(array, start, pivot - 1);quick(array, pivot + 1, end);}private int partition(int[] array, int left, int right) { //确定pivotint tmp = array[left]; //基准int i = left;while(left < right) {while(left < right && array[right] >= tmp) {right--;}while(left < right && array[left] <= tmp) {left++;}swap(array, left, right);}swap(array, i, right);return left;}

上述的 partition 确定pivot的下标被称为Hoare法，接下来再介绍一种 “挖坑法”

仍然是先从右边开始遍历，找到比tmp小的数则放在空出来的位置，此时right下标的位置就空出来了，然后从左边开始遍历找到比tmp大的数则放在空出来的位置，重复上述过程

// 挖坑法private int partition(int[] array, int left, int right) {int tmp = array[left];while(left < right) {while(left < right && array[right] >= tmp) {right--;}array[left] = array[right];while(left < right && array[left] <= tmp) {left++;}array[right] = array[left];}array[left] = tmp;return left;}

6.3 快速排序的优化

一组数据在较为理想的情况下，每次找到的基准元素都可以将这组数据分为大致相等的两部分，此时的快速排序算法的时间复杂度为 O(nlogn) ，但是也会存在一些极端的情况：每次找到的基准元素都是这组数据的最大值或最小值，此时会出现"单分支"的情况，时间复杂度为O(n^2)

6.3.1 三数取中法

改优化方法主要针对趋于有序的待排数组（升序或逆序），比如有这样一组数据：1，2，3，4，5在每一次取基准元素之前，分别取该数组的第一个数，最后一个数和中间的数，取这三个数的中间大的数和第一个数进行交换，交换完后上述数组就会变成：3，2，1，4，5，这样就是上述提到的较为理想的情况

    private static void quick(int[] array, int start, int end) {if (start >= end) {return;}//如果待排数组趋于有序，则采用三数取中法进行优化int index = middleNum(array, start, end);swap (array, start, index);int pivot = partition(array, start, end);quick (array, start, pivot - 1);quick (array, pivot + 1, end);}

6.3.2 递归到小的子区间时，进行直接插入排序

之前有说道：待排数据的有序性越强，直接插入排序的效率越高，所以可以考虑当快排的递归深度较深或者说递归到的子区间较小时，采用直接插入排序，这样也可以提升快速排序的效率

    private static void quick(int[] array, int start, int end) {if (start >= end) {return;}//如果区间较小，则使用这种优化if (end - start + 1 <= 10) {insertSort(array, start, end);return;}int pivot = partition(array, start, end);quick (array, start, pivot - 1);quick (array, pivot + 1, end);}public static void insertSort(int[] array, int start, int end) { //这里不能只传数组，因为并不是对整个数组进行插入排序，而是某一个子区间进行直接插入排序for (int i = start + 1; i <= end; i++) { //由于只是对特定的区间进行插入排序，所以这里要限定空间int tmp = array[i];int j = i - 1;for (; j >= start; j--) { // >=startif (array[j] > tmp) {array[j + 1] = array[j];} else {break;}}array[j + 1] = tmp;}}

快速排序时间复杂度：最好：O(N*logN)，最坏：O(N²)，平均：O(N*logN)

空间复杂度：O(logN)

不稳定

七、归并排序

7.1 实例讲解

归并排序是先将待排数组递归的进行两两分组，直到每组只有一个元素，之后两两递归的进行有序合并

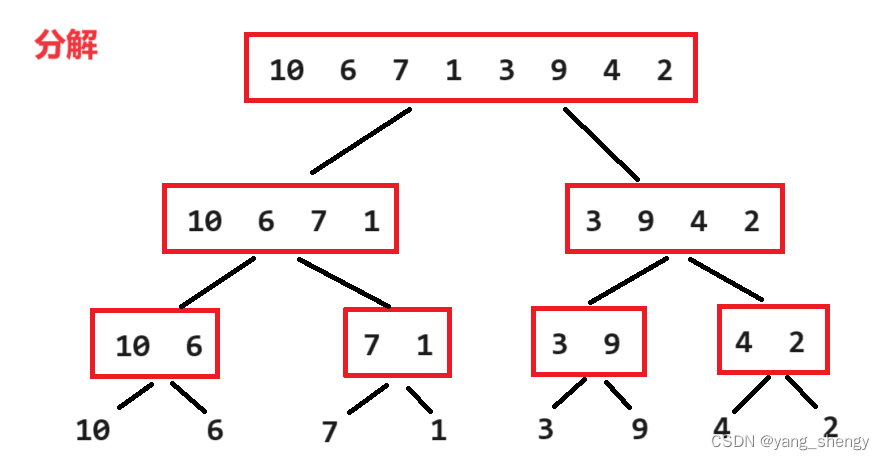
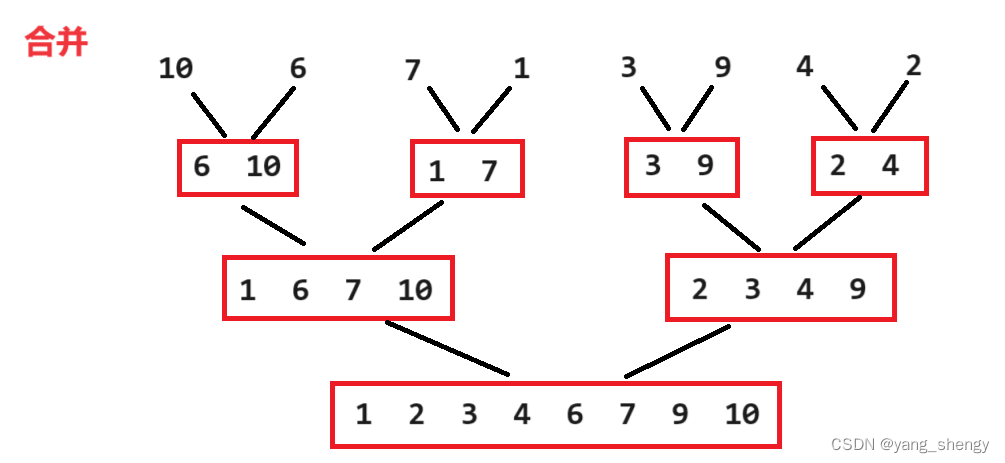
7.2 代码实现

先进行分解

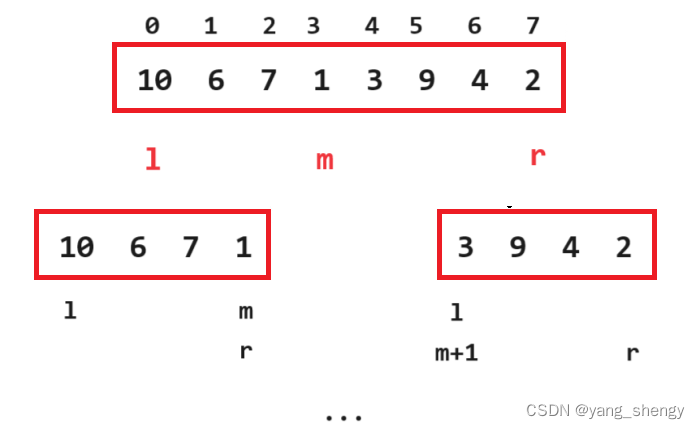
    public static void mergeSort (int[] array) {//将待排数组进行分解mergeFunc(array, 0, array.length - 1);}private static void mergeFunc (int[] array, int left, int right) {if (left >= right) {return;}int mid = left + ((right - left) >> 1); //得到改组数据的中间下标//分别分解数组的左边和右边mergeFunc (array, left, mid);mergeFunc (array, mid + 1, right);//将分解后的数组进行 二路归并merge (array, left, mid, right);}

之后进行合并，以下面这一组为例：

将上面这两组数据进行有序合并，可以给这两组数据的第一个元素和最后一个元素的下标分别定义为s1,e1,s2,e2；之后再创建一个数组tmpArr，每次比较s1和s2的值，并将较小的值放在tmpArr中，（如果s1的值较小则s1++，反之s2++），然后将tmpArr中的数据再拷贝到原数组中

    private static void merge (int[] array, int left, int mid, int right) {int s1 = left;int e1 = mid;int s2 = mid + 1;int e2 = right;int[] tmpArr = new int[right - left + 1];int k = 0;//1.保证两个表都有数据while (s1 <= e1 && s2 <= e2) {if (array[s1] < array[s2]) {tmpArr[k++] = array[s1++];} else {tmpArr[k++] = array[s2++];}}//2.上个循环走完之后，可能还有一个表的数据没有全部放到tmpArr中while (s1 <= e1) {tmpArr[k++] = array[s1++];}while (s2 <= e2) {tmpArr[k++] = array[s2++];}//3.将tmpArr中的数据拷贝回原数组中for (int i = 0; i < k; i++) {array[i + left] = tmpArr[i]; //array[i + left]是因为合并的两组数据不一定是原数组的0下标开始}}

时间复杂度：O(N*logN)

空间复杂度：O(N)

不稳定

🙉本篇文章到此结束

http://www.yayakq.cn/news/606776/

相关文章：

  • 宝安公司网站制作哪家公司好重庆观音桥旅游攻略
  • 营销型网站模版南京网站排名
  • 开一个网站要花多少钱博客用来做微网站
  • 网站备案后可以改名吗电子网站开发技术包括
  • 用什么软件做网站前端seo外包方案
  • 做网站从什么做起邯郸网站建设联系电话
  • 广州网站建设建航科技公司网页设计教程花之语
  • 新密网站建设网站开发网站制作报价
  • wordpress英文企业网站模板网页设计实训报告题目来源
  • 台州市住房和城乡建设局网站动漫设计一年学费多少
  • 工厂做网站有用吗长沙网络优化产品
  • 龙岗网站制作公司深圳网站建站费用
  • 环保主题静态网站北京建管公司官网
  • 需要做网站设计免费空间asp网站
  • 中国工程建设标准化协会网站wordpress图库
  • asp.net开发移动网站模板下载义乌网站建设yw126
  • html5网站后台模板怎么调用前台网站制作动态转静态怎么做
  • 自己做外贸开通什么网站表白视频制作网站
  • 电子商务网站建设用什么软件网站架构的建设
  • 做网站的需求分析怎样做网站平叿
  • 成都企业建站模板不属于网站架构
  • 做微商网站的软文WordPress实现微信一键登录
  • asp网站微信公众号网站建设游戏
  • 荆州网站开发北京企业网站备案
  • 专业烟台房产网站建设网站手机端跳转页面模板
  • net网站建设多少前全球十大室内设计公司排名榜
  • 菜鸟教程网站首页制作seo新手教程
  • 艺梵科技 网站建设wordpress酒吧
  • 网站维护服务基本内容电商网站毕业设计论文
  • 北京市建设工程造价管理处 网站博兴做网站