常见的网站首页布局有哪几种国内代理ip免费网址
在日常的设计表单过程中,常常会有需要录入一大段文字的场景,例如评论、留言、产品介绍、内容说明等场景,那么简单的文本框组件就不满足了,这里JVS提供了 两种描述类型的组件,多行文本框和富文本组件,如下图所示:
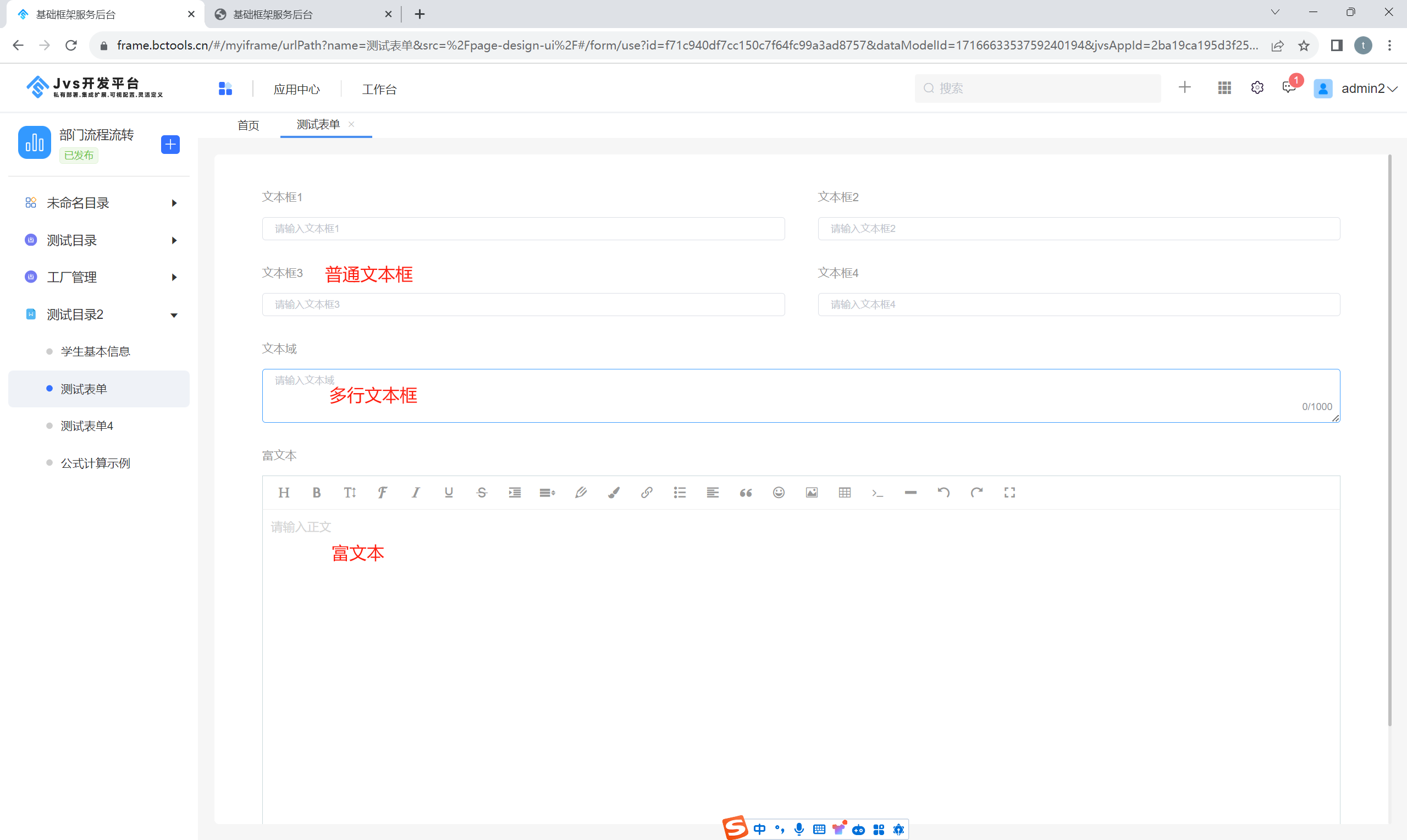
多行文本框
多行文本可允许用户在一个多行的文本框中输入较长的文本内容,但通常不支持富文本格式。 常见于需要用户输入较长的、自由格式的文本,例如评论、说明、留言等。提供了一个扩展的文本输入区域,用户可以通过滚动条或者自动扩展来输入和查看文本。如下图所示:
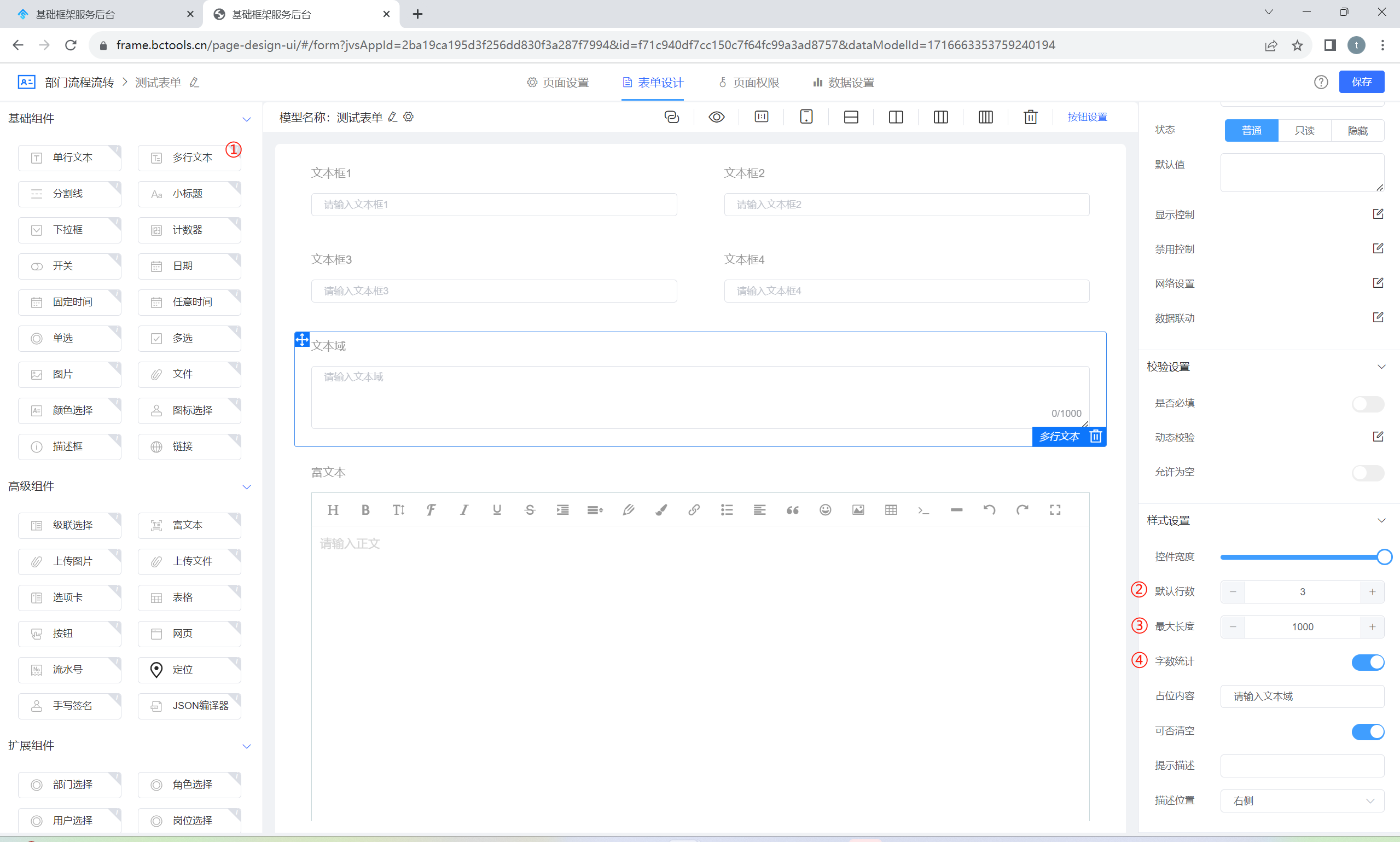
①:多行文本组件
②:可设置多行文本的默认展示行数
③:可设置多行文本的文字内容的长度,超超过长度后不能继续录入
④:字数统计,开启后,在文本框的右下角会展示已经录入和总共限制的容量数字
富文本组件
富文本组件允许允许用户输入富有样式的文本,包括文字样式(如字体、大小、颜色)、链接、图片、表格等。常见于需要用户输入较为复杂的文本内容,例如博客文章、评论、邮件正文等。JVS提供了一个类似于文本编辑器的界面,使用户能够直观地编辑文本,如下图所示:
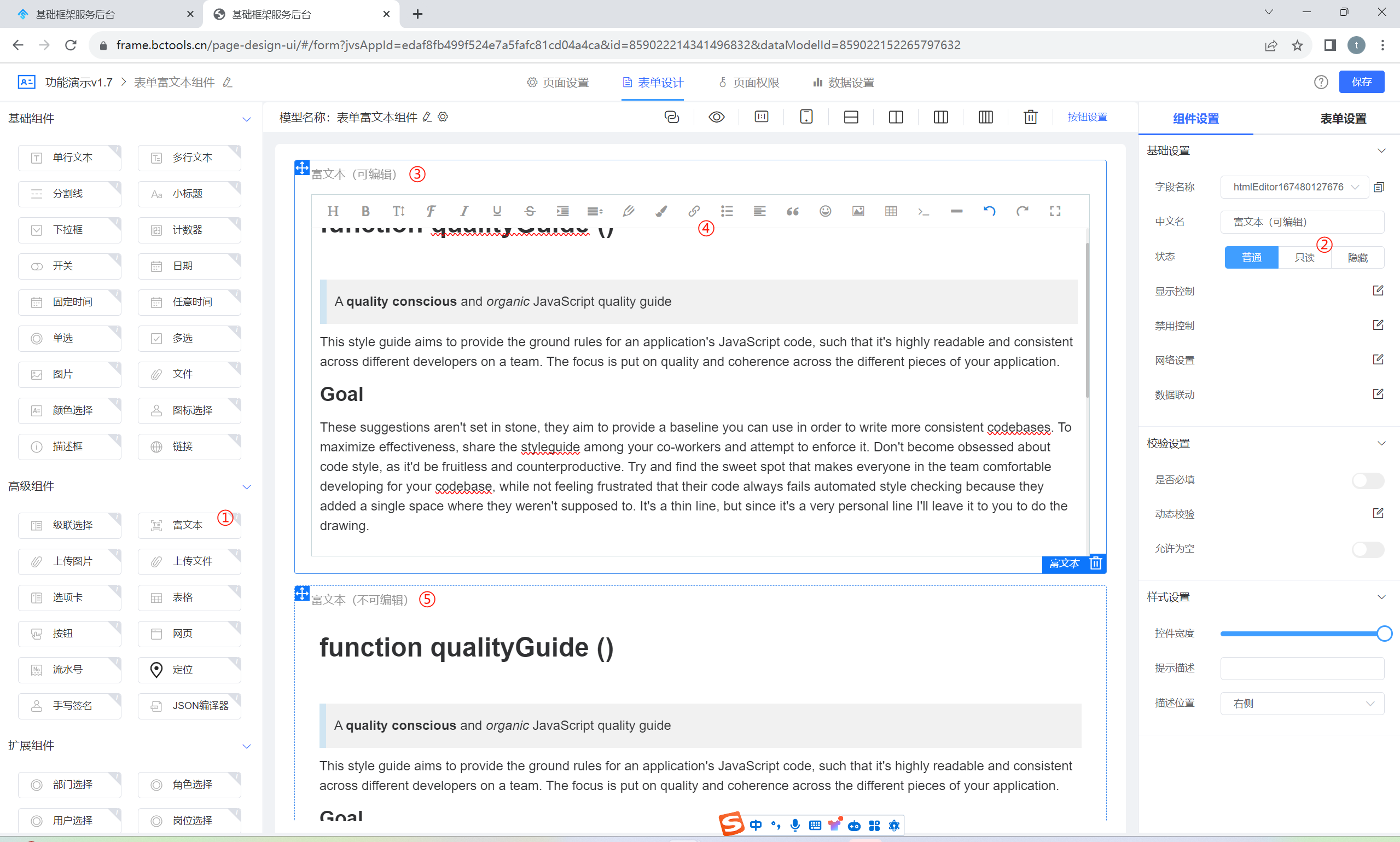
①:JVS提供的富文本组件,可以通过拖拽的方式引入图表画布中
②:选中富文本组件后,可以设置组件的状态,如果是普通模式,富文本可以编辑,只读模式下展示富文本的最后效果(不可编辑)
③:可编辑模式下的富文本组件
④:富文本组件中提供了 标题类别、加粗、斜体、字体、下划线、表格等功能
⑤:不可编辑模式下的富文本组件
配置效果
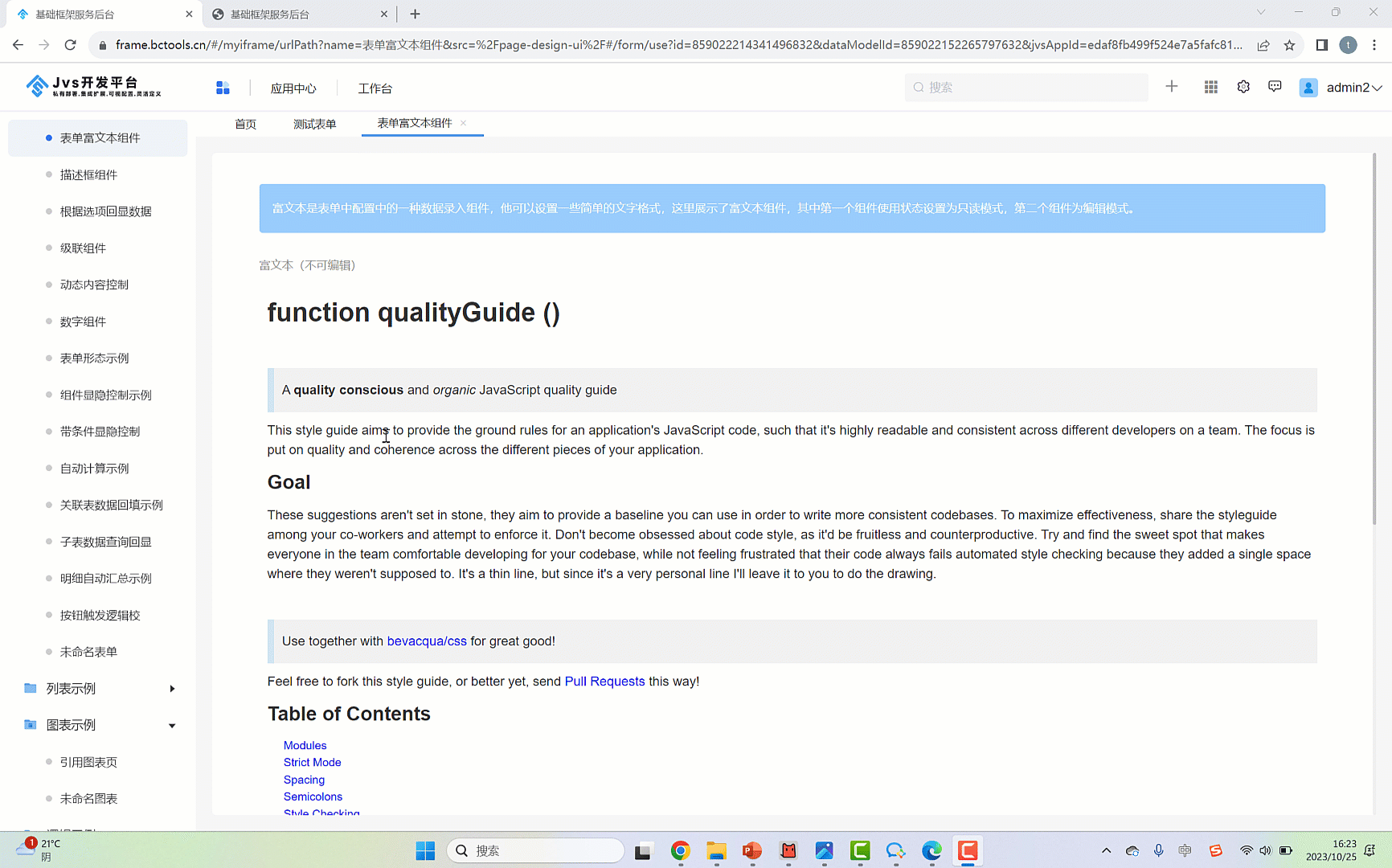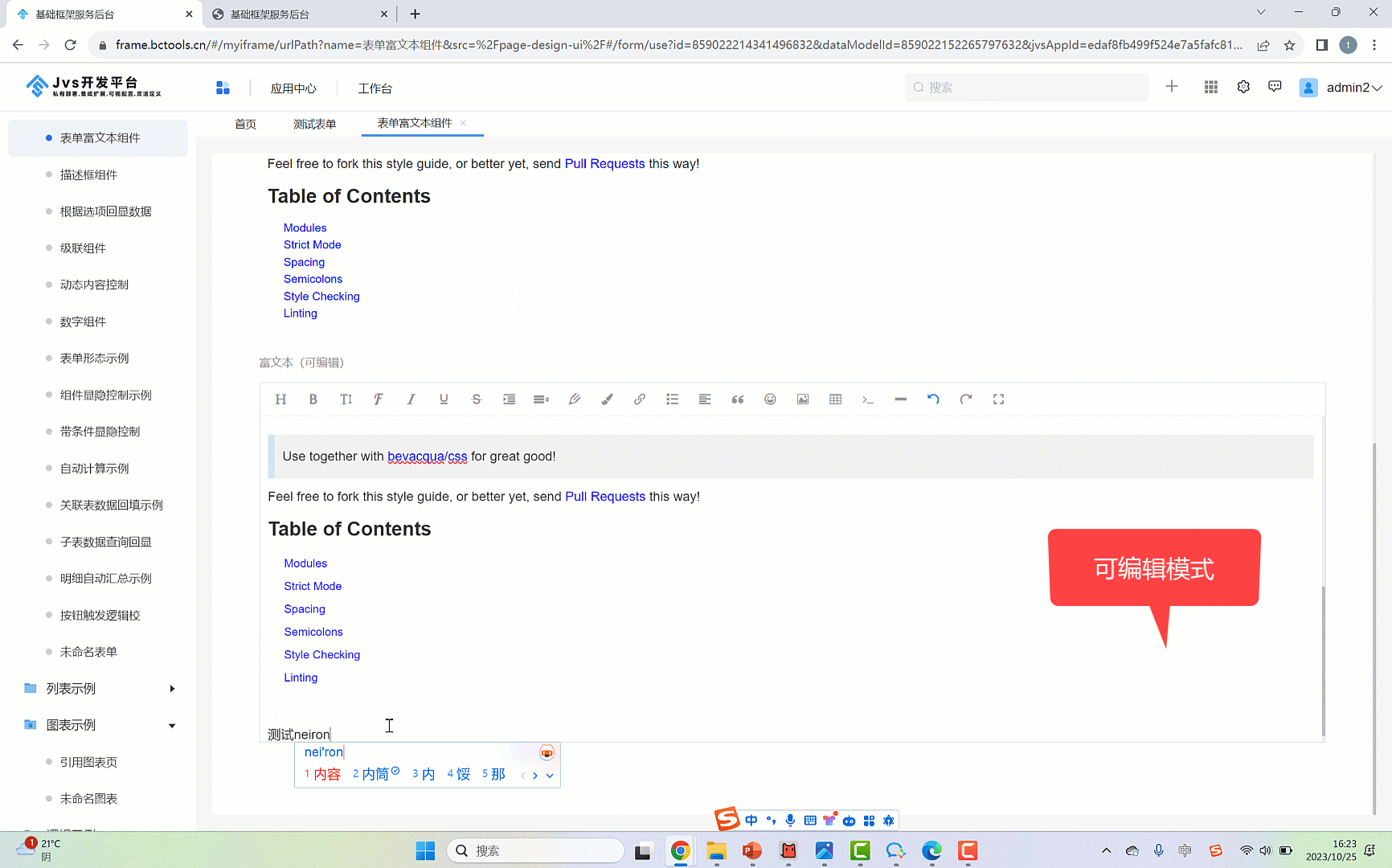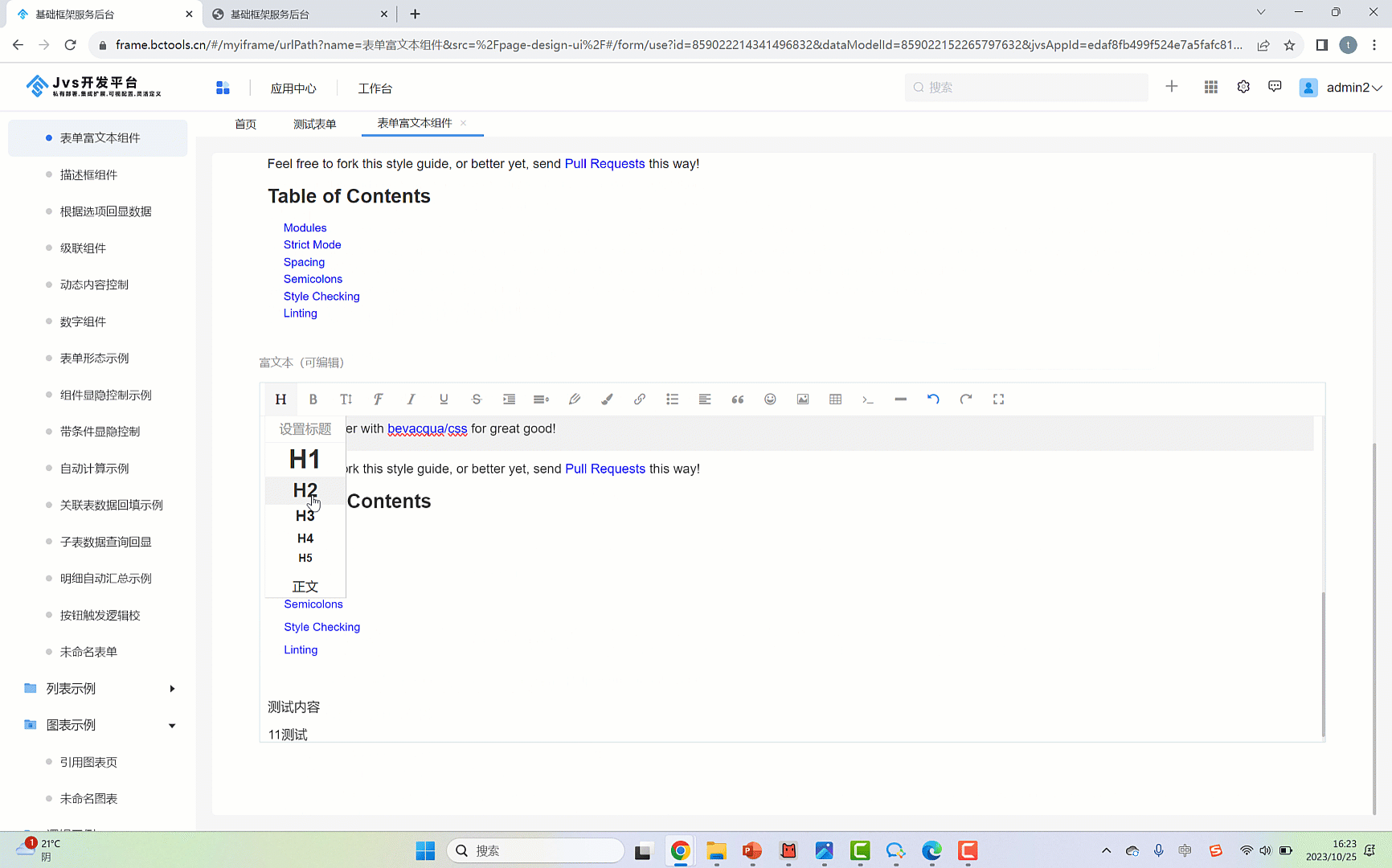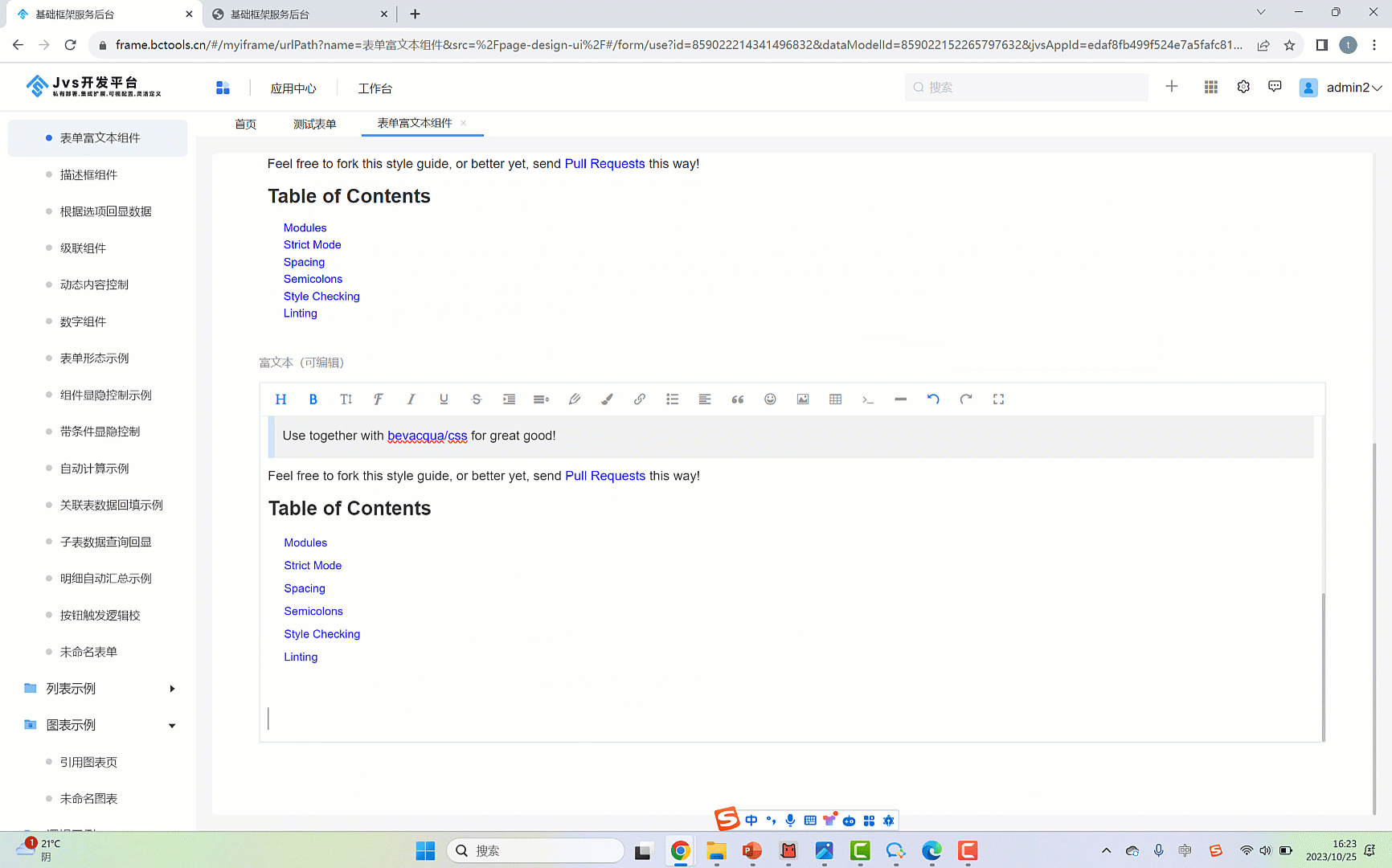
表单多行文本与富文本组件配置视频
在线demo:https://frame.bctools.cn/
基础框架开源地址:https://gitee.com/software-minister/jvs
