安全的网站建房价在2022年大跌
目录
一、创建Web页面浏览器
1.示例源码
2.生成效果
二、局域网聊天程序
1.类
2.服务器端
3.客户端
一、创建Web页面浏览器
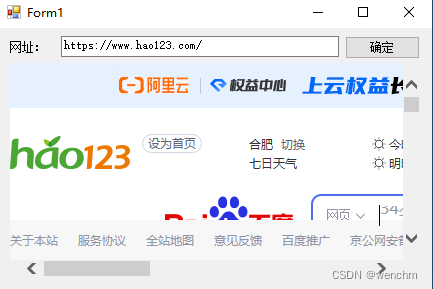
TextBox 控件用来输入要浏览的网页地址,Button控件用来执行浏览网页操作, WebBrowser控件用来显示要浏览的网页。这个控件目前只能在.NET Framework 4.8下使用,.NET8.0不支持了。
在使用WebBrowser 类时会占用大量资源,当使用完后必须调用 Dispose() 方法,以确保及时释放所有资源。
1.示例源码
// WebBrowser
// 这个控件目前只能在.NET Framework 4.8下使用,.NET8.0不支持了
// 在“网址”文本框中输入要浏览的网页地址,
// 按Enter键或单击“转到”按钮,即可浏览指定的网页。
using System;
using System.Windows.Forms;namespace _WebBrowser
{public partial class Form1 : Form{public Form1(){InitializeComponent();}private void WebBrowser1_DocumentCompleted(object sender, WebBrowserDocumentCompletedEventArgs e){}/// <summary>/// 创建一个Uri类型的变量,用来存储要浏览的网页地址/// 在WebBrowser控件中显示指定的网页/// </summary>private void Button1_Click(object sender, EventArgs e){Uri address = new Uri(textBox1.Text);webBrowser1.Url = address;}private void Form1_Load(object sender, EventArgs e){label1.Text = "网址:";button1.Text = "确定";Text = "WebBrowser";}private void TextBox1_KeyPress(object sender, KeyPressEventArgs e){if (e.KeyChar == 13){if (textBox1.Text != ""){Button1_Click(sender, e); //判断是否按下Enter键}}}}
}
// Form1.Designer.cs
namespace _WebBrowser
{partial class Form1{/// <summary>/// 必需的设计器变量。/// </summary>private System.ComponentModel.IContainer components = null;/// <summary>/// 清理所有正在使用的资源。/// </summary>/// <param name="disposing">如果应释放托管资源,为 true;否则为 false。</param>protected override void Dispose(bool disposing){if (disposing && (components != null)){components.Dispose();}base.Dispose(disposing);}#region Windows 窗体设计器生成的代码/// <summary>/// 设计器支持所需的方法 - 不要修改/// 使用代码编辑器修改此方法的内容。/// </summary>private void InitializeComponent(){this.label1 = new System.Windows.Forms.Label();this.textBox1 = new System.Windows.Forms.TextBox();this.button1 = new System.Windows.Forms.Button();this.panel1 = new System.Windows.Forms.Panel();this.webBrowser1 = new System.Windows.Forms.WebBrowser();this.panel1.SuspendLayout();this.SuspendLayout();// // label1// this.label1.AutoSize = true;this.label1.Location = new System.Drawing.Point(10, 13);this.label1.Name = "label1";this.label1.Size = new System.Drawing.Size(41, 12);this.label1.TabIndex = 0;this.label1.Text = "label1";// // textBox1// this.textBox1.Location = new System.Drawing.Point(63, 8);this.textBox1.Name = "textBox1";this.textBox1.Size = new System.Drawing.Size(278, 21);this.textBox1.TabIndex = 1;this.textBox1.KeyPress += new System.Windows.Forms.KeyPressEventHandler(this.TextBox1_KeyPress);// // button1// this.button1.Location = new System.Drawing.Point(347, 8);this.button1.Name = "button1";this.button1.Size = new System.Drawing.Size(75, 23);this.button1.TabIndex = 2;this.button1.Text = "button1";this.button1.UseVisualStyleBackColor = true;this.button1.Click += new System.EventHandler(this.Button1_Click);// // panel1// this.panel1.Controls.Add(this.webBrowser1);this.panel1.Location = new System.Drawing.Point(12, 35);this.panel1.Name = "panel1";this.panel1.Size = new System.Drawing.Size(410, 214);this.panel1.TabIndex = 3;// // webBrowser1// this.webBrowser1.Dock = System.Windows.Forms.DockStyle.Fill;this.webBrowser1.Location = new System.Drawing.Point(0, 0);this.webBrowser1.MinimumSize = new System.Drawing.Size(20, 20);this.webBrowser1.Name = "webBrowser1";this.webBrowser1.Size = new System.Drawing.Size(410, 214);this.webBrowser1.TabIndex = 4;// // Form1// this.AutoScaleDimensions = new System.Drawing.SizeF(6F, 12F);this.AutoScaleMode = System.Windows.Forms.AutoScaleMode.Font;this.ClientSize = new System.Drawing.Size(434, 261);this.Controls.Add(this.panel1);this.Controls.Add(this.button1);this.Controls.Add(this.textBox1);this.Controls.Add(this.label1);this.Name = "Form1";this.StartPosition = System.Windows.Forms.FormStartPosition.CenterScreen;this.Text = "Form1";this.Load += new System.EventHandler(this.Form1_Load);this.panel1.ResumeLayout(false);this.ResumeLayout(false);this.PerformLayout();}#endregionprivate System.Windows.Forms.Label label1;private System.Windows.Forms.TextBox textBox1;private System.Windows.Forms.Button button1;private System.Windows.Forms.Panel panel1;private System.Windows.Forms.WebBrowser webBrowser1;}
}2.生成效果
二、局域网聊天程序
Windows窗体应用,在解决方案下添加一个类和两个Windows窗体应用项目,其中,类文件用来封装接收信息和发送信息的方法,两个Windows窗体应用项目分别用来作为聊天程序的服务器端和客户端。
框架:.NET Framework 4.8,无论什么框架可能会遇到MessageBox.Show 方法不被支持,请按作者提供的方法去解决。
C#中的警告CS0120、CS0176、CS0183、CS0618、CS0649、CS8600、CS8601、CS8602、CS8604、CS8625、CS8618、CS0103及处理-CSDN博客 https://blog.csdn.net/wenchm/article/details/134606735?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22134606735%22%2C%22source%22%3A%22wenchm%22%7D http://C#%E4%B8%AD%E7%9A%84%E8%AD%A6%E5%91%8ACS0120%E3%80%81CS0176%E3%80%81CS0183%E3%80%81CS0618%E3%80%81CS0649%E3%80%81CS8600%E3%80%81CS8601%E3%80%81CS8602%E3%80%81CS8604%E3%80%81CS8625%E3%80%81CS8618%E3%80%81CS0103%E5%8F%8A%E5%A4%84%E7%90%86-CSDN%E5%8D%9A%E5%AE%A2%20%20https://blog.csdn.net/wenchm/article/details/134606735?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22134606735%22%2C%22source%22%3A%22wenchm%22%7D
http://C#%E4%B8%AD%E7%9A%84%E8%AD%A6%E5%91%8ACS0120%E3%80%81CS0176%E3%80%81CS0183%E3%80%81CS0618%E3%80%81CS0649%E3%80%81CS8600%E3%80%81CS8601%E3%80%81CS8602%E3%80%81CS8604%E3%80%81CS8625%E3%80%81CS8618%E3%80%81CS0103%E5%8F%8A%E5%A4%84%E7%90%86-CSDN%E5%8D%9A%E5%AE%A2%20%20https://blog.csdn.net/wenchm/article/details/134606735?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22134606735%22%2C%22source%22%3A%22wenchm%22%7D
.NET 8.0框架下我也重建了该项目,遭遇到的MessageBox.Show()CS0103红色警告。百般折腾,没有解决得了同样的问题。网友感兴趣的话可以试试,如果解决了,把经验分享一下。
1.类
// 聊天室,解决方案下建立的公共类库
using System.Net.Sockets;
using System.Net;
using System.Text;
using System;
using System.Windows;
using System.Windows.Forms;namespace StartListener
{public class Class1{public const int port = 11000;public void StartListener(){UdpClient udpclient = new UdpClient(port); //设置端口号IPEndPoint ipendpoint = new IPEndPoint(IPAddress.Any, port);//将网络端点表示为IP地址和端口号try{while (true){byte[] bytes = udpclient.Receive(ref ipendpoint);string strlP = "信息来自" + ipendpoint.Address.ToString();string strlnfo = Encoding.GetEncoding("gb2312").GetString(bytes, 0, bytes.Length);MessageBox.Show(strlnfo, strlP);}}catch (Exception e){MessageBox.Show(e.ToString());}finally{udpclient.Close();}}public static string Send(string strServer, string strContent){Socket socket = new Socket(AddressFamily.InterNetwork, SocketType.Dgram, ProtocolType.Udp);IPAddress ipaddress = IPAddress.Parse(strServer); //将输入的字符串转换为IP地址 byte[] btContent = Encoding.GetEncoding("gb2312").GetBytes(strContent); //将发送的内容存储到byte数组中IPEndPoint ipendpoint = new IPEndPoint(ipaddress, 11000);socket.SendTo(btContent, ipendpoint);socket.Close();return "发送成功";}}
}
2.服务器端
// 服务器端,要增加对公共类的引用
using StartListener;
using System;
using System.Windows.Forms;namespace ChatServer
{public partial class Form1 : Form{readonly Class1 class1 = new Class1();public Form1(){InitializeComponent();}/// <summary>/// 隐藏当前窗体//调用公共类中的方法接收信息/// </summary>private void Form1_Load(object sender, EventArgs e){Hide();class1.StartListener();}}
}
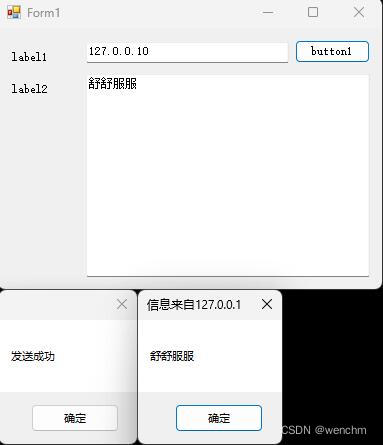
3.客户端
// 客户端端,要增加对公共类的引用
using StartListener;
using System.Diagnostics;
using System;
using System.Windows.Forms;namespace ChatClient
{public partial class Form1 : Form{ Process myProcess;public Form1(){InitializeComponent();}/// <summary>/// 开启服务器/// 要把服务器端生成的.exe文件复制到客户端当前文件夹下/// 并且文件名要修改为实际生成的文件名/// </summary>private void Form1_Load(object sender, EventArgs e){myProcess = Process.Start("ChatServer.exe"); }private void Button1_Click(object sender, EventArgs e){string send = Class1.Send(textBox1.Text, textBox2.Text);MessageBox.Show(send); //发送信息//textBox2.Text = string.Empty;textBox2.Focus();}private void TextBox1_KeyPress(object sender, KeyPressEventArgs e){if (e.KeyChar == 13)textBox2.Focus();}private void TextBox2_KeyPress(object sender, KeyPressEventArgs e){if (e.KeyChar == 13)button1.Focus();}private void Form1_FormClosing(object sender, FormClosingEventArgs e){myProcess.Kill();}}
}
// Form1.Designer.cs
namespace ChatClient
{partial class Form1{/// <summary>/// 必需的设计器变量。/// </summary>private System.ComponentModel.IContainer components = null;/// <summary>/// 清理所有正在使用的资源。/// </summary>/// <param name="disposing">如果应释放托管资源,为 true;否则为 false。</param>protected override void Dispose(bool disposing){if (disposing && (components != null)){components.Dispose();}base.Dispose(disposing);}#region Windows 窗体设计器生成的代码/// <summary>/// 设计器支持所需的方法 - 不要修改/// 使用代码编辑器修改此方法的内容。/// </summary>private void InitializeComponent(){this.button1 = new System.Windows.Forms.Button();this.label1 = new System.Windows.Forms.Label();this.label2 = new System.Windows.Forms.Label();this.textBox1 = new System.Windows.Forms.TextBox();this.textBox2 = new System.Windows.Forms.TextBox();this.SuspendLayout();// // button1// this.button1.Location = new System.Drawing.Point(297, 12);this.button1.Name = "button1";this.button1.Size = new System.Drawing.Size(75, 23);this.button1.TabIndex = 0;this.button1.Text = "button1";this.button1.UseVisualStyleBackColor = true;this.button1.Click += new System.EventHandler(this.Button1_Click);// // label1// this.label1.AutoSize = true;this.label1.Location = new System.Drawing.Point(12, 23);this.label1.Name = "label1";this.label1.Size = new System.Drawing.Size(41, 12);this.label1.TabIndex = 1;this.label1.Text = "label1";// // label2// this.label2.AutoSize = true;this.label2.Location = new System.Drawing.Point(12, 55);this.label2.Name = "label2";this.label2.Size = new System.Drawing.Size(41, 12);this.label2.TabIndex = 2;this.label2.Text = "label2";// // textBox1// this.textBox1.Location = new System.Drawing.Point(88, 14);this.textBox1.Name = "textBox1";this.textBox1.Size = new System.Drawing.Size(203, 21);this.textBox1.TabIndex = 3;this.textBox1.KeyPress += new System.Windows.Forms.KeyPressEventHandler(this.TextBox1_KeyPress);// // textBox2// this.textBox2.Location = new System.Drawing.Point(88, 46);this.textBox2.Multiline = true;this.textBox2.Name = "textBox2";this.textBox2.Size = new System.Drawing.Size(284, 203);this.textBox2.TabIndex = 4;this.textBox2.KeyPress += new System.Windows.Forms.KeyPressEventHandler(this.TextBox2_KeyPress);// // Form1// this.AutoScaleDimensions = new System.Drawing.SizeF(6F, 12F);this.AutoScaleMode = System.Windows.Forms.AutoScaleMode.Font;this.ClientSize = new System.Drawing.Size(384, 261);this.Controls.Add(this.textBox2);this.Controls.Add(this.textBox1);this.Controls.Add(this.label2);this.Controls.Add(this.label1);this.Controls.Add(this.button1);this.Name = "Form1";this.StartPosition = System.Windows.Forms.FormStartPosition.CenterScreen;this.Text = "Form1";this.FormClosing += new System.Windows.Forms.FormClosingEventHandler(this.Form1_FormClosing);this.Load += new System.EventHandler(this.Form1_Load);this.ResumeLayout(false);this.PerformLayout();}#endregionprivate System.Windows.Forms.Button button1;private System.Windows.Forms.Label label1;private System.Windows.Forms.Label label2;private System.Windows.Forms.TextBox textBox1;private System.Windows.Forms.TextBox textBox2;}
}