保险公司网站查询韩国做 mp4下载网站
声场合成是指在房间内的麦克风阵列上,根据来自房间内其他位置的声源信号,合成每个麦克风的音频信号。它是评估语音/音频通信设备性能指标的关键任务,因为它是一种成本效益高的方法,用于数据生成以替代真实的数据收集,后者通常是缓慢的、昂贵的,并且容易出错的过程。
1 现有声场合成方法的局限性
1.1 基于测量的方法
- 准确,但成本高,需要大量人力进行测量。
- 需要对每个源/接收器位置组合和每种不同形状的设备进行重复测量。
- 需要设备硬件,不适合硬件开发阶段。
1.2 基于模拟的方法
- 通过计算声学波方程来估计房间脉冲响应 (RIR)。
- 需要大量的计算资源,尤其是在宽带频谱下。
- 需要对每种不同形状的设备进行重复模拟。
2 新方法
本文提供一种新方法,它结合了经验方法和模拟方法,为声场合成提供了两种方法之间的平衡。它将声场分解为两个独立的成分:房间成分和设备成分。整体声场是两个成分的复合映射。
2.1 理论基础
声学平面波是齐次亥姆霍兹方程的特征函数,是分析波动方程的强大工具。远场点源产生的声场可以用声学平面波很好地近似。
2.1.1 平面波分解
- 平面波分解 (PWD) 是一种将声场近似为不同方向和权重的平面波叠加的方法。
- PWD 可以近似齐次亥姆霍兹方程的局部解,并用于声场重建和声场再现等应用。
2.1.2 平面波分解的稀疏性
- 平面波分解的系数 αl 通常具有稀疏性,即只有少量平面波对声场有显著贡献。
- 稀疏性为使用稀疏恢复技术计算平面波分解提供了理论基础。
2.1.3 平面波分解的应用
- 声场重建:通过测量麦克风阵列上的声场,可以计算平面波分解,并重建声源位置和声源信号。
- 声场再现:通过控制扬声器的声场,可以再现特定的声场,例如音乐会现场的声音。
- 声场合成:将平面波分解应用于声场合成,可以生成麦克风阵列上的声场信号。
2.2 设备声学字典
设备声学字典是一组向量,每个向量表示设备麦克风阵列在受到特定方向和频率的声学平面波照射时的总声场。
2.2.1 获取方法
- 无响室测量:在无响室中,使用单频远场声源照射设备,并测量麦克风阵列上的声场,得到设备声学字典。
- 数值模拟:使用有限元法 (FEM) 或边界元法 (BEM) 等数值方法,在设备表面上求解亥姆霍兹方程,得到设备声学字典。
2.2.2 作用
- 设备声学字典是声场合成框架中连接房间分量和设备分量的桥梁。
- 通过将房间分量的平面波分解结果与设备声学字典相结合,可以合成设备麦克风阵列上的声场信号。
- 设备声学字典可以用于多种设备,无需针对每种设备重新计算。
2.2.3 数值模拟的细节
- 使用 FEM 或 BEM 等数值方法,在设备表面上求解亥姆霍兹方程,得到总声场。
- 设备表面被建模为声硬边界。
- 为了模拟开放边界,使用完美匹配层 (PML) 技术消除内部域的反射和折射。
- 使用标准偏微分方程求解软件包进行模拟,并通过与无响室测量结果进行比较验证模拟的准确性。
2.2.4 设备声学字典的应用
- 声场合成:将房间分量的平面波分解结果与设备声学字典相结合,合成设备麦克风阵列上的声场信号。
- 麦克风阵列处理:使用设备声学字典设计波束形成器,提高波束形成性能。
- 声源定位和分离:利用设备声学字典进行声源定位和分离。
- 去混响:使用设备声学字典进行去混响处理。
2.3 技术框架
2.3.1 框架组成
- 房间分量:将房间内某点的声场表示为声学平面波的叠加,通过使用大麦克风阵列进行测量和稀疏恢复技术计算得到平面波分解结果。
- 设备分量:计算设备表面对于声学平面波的响应,得到设备声学字典。
- 合成分量:将房间分量的平面波分解结果与设备分量的设备声学字典相结合,合成设备麦克风阵列上的声场信号。
2.3.2 框架步骤
2.3.2.1 房间分量计算
- 使用大麦克风阵列(例如 EigenMike)进行测量,获取房间内某点的声场信号。
- 使用稀疏恢复技术对测量信号进行平面波分解,得到平面波的方向和权重。
- 重复以上步骤,为每个房间和每个位置生成房间分量的平面波分解结果,形成房间数据库。
2.3.2.2 设备分量计算
使用无响室测量或数值模拟,计算设备表面对于声学平面波的响应,得到设备声学字典。
2.3.2.3 声场合成
- 选择房间数据库中与目标位置对应的房间分量平面波分解结果。
- 将设备声学字典与房间分量的平面波分解结果相结合,合成设备麦克风阵列上的声场信号。
2.3.3 框架优势
- 分离房间声学和设备声学:将房间声学和设备声学分离,简化了声场合成的复杂性,并实现了组件的复用。
- 减少测量/模拟开销:房间分量只需要进行一次测量,设备分量只需要进行一次计算,减少了测量/模拟的开销。
- 提高计算效率:设备分量的计算可以在无响室中进行,并高度并行化,提高了计算效率。
- 提高准确性:设备声学字典能够捕捉设备表面对于声学平面波的散射效应,提高了声场合成的准确性。
2.3.4 框架应用
- 数据生成:生成合成数据,用于评估设备性能指标(例如误识率、词错误率)和训练深度学习声学模型。
- 麦克风阵列处理:使用设备声学字典设计波束形成器,提高波束形成性能。
- 声源定位和分离:利用设备声学字典进行声源定位和分离。
- 去混响:使用设备声学字典进行去混响处理。
3 实验验证
本文通过三组实验来验证提出的声场合成框架的有效性
3.1 平面波分解验证
- 使用 EigenMike 麦克风阵列记录两个不同的源信号,并使用稀疏恢复技术进行平面波分解。
- 验证不同数量的平面波对声场重建误差的影响。
结果表明,少量平面波(例如 20-30 个)就能够以小于 -20 dB 的误差重建声场,证明了平面波分解的有效性。
3.2 房间脉冲响应(RIR)验证
- 在三个不同的房间内进行实验,每个房间包含 24 个不同的位置。
- 将 EigenMike 麦克风阵列与四种不同形状和麦克风阵列大小的设备进行共位。
- 使用提出的框架计算每个位置的 RIR,并与实测 RIR 进行比较。
结果表明,合成 RIR 与实测 RIR 在所有频率上都高度相似,重建信号噪声比(SNR)为 19-23 dB,证明了 RIR 计算的准确性。
3.3 高级指标评估
- 使用合成 RIR 和实测 RIR 对关键词误识率(FRR)进行评估。
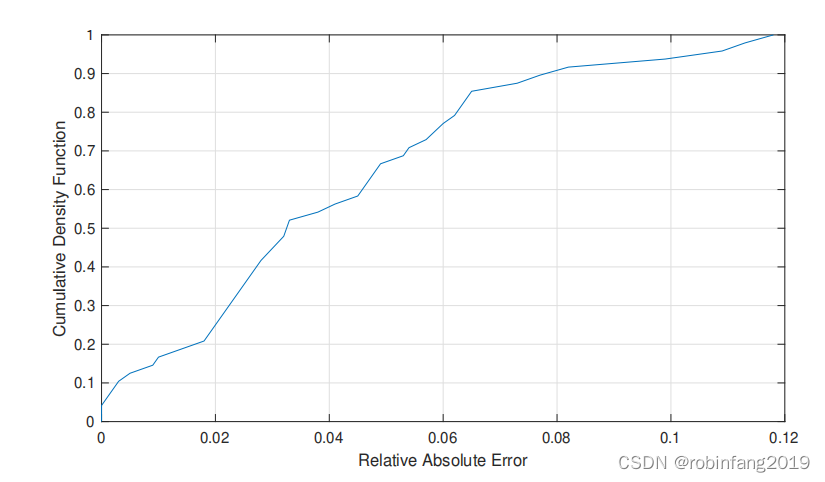
- 计算实测 FRR 和合成 FRR 之间的相对误差。
结果表明,实测 FRR 和合成 FRR 之间的相对误差小于 10%,证明了框架在评估高级指标方面的有效性。