玉树州wap网站建设公司南京产品网站建设收费
问题描述:
在登录页面加载完成后通过axios请求后端验证码接口(这时后端会生成一个session用于保存验证码数值),当输入完用户名、密码、验证码后请求登录接口,报错验证码输入错误,打印后端保存验证码的session值,返回null
解决方法:
前端对axios进行配置,允许跨域携带cookie
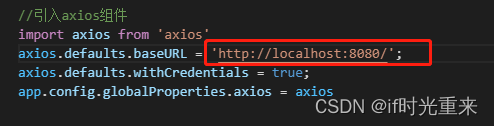
import axios from 'axios'
axios.defaults.withCredentials=true;
后端跨域配置(以下仅供参考,具体请自行百度):
@Configuration
public class CorsConfig {@Beanpublic CorsFilter corsFilter() {final UrlBasedCorsConfigurationSource source = new UrlBasedCorsConfigurationSource();final CorsConfiguration corsConfiguration = new CorsConfiguration();corsConfiguration.addAllowedHeader("*");corsConfiguration.addAllowedOrigin("*");corsConfiguration.addAllowedMethod("*");//关键配置corsConfiguration.setAllowCredentials(true);source.registerCorsConfiguration("/**", corsConfiguration);return new CorsFilter(source);}
}
springboot
package com.server.server_demo;
import org.springframework.context.annotation.Configuration;
import org.springframework.web.servlet.config.annotation.CorsRegistry;
import org.springframework.web.servlet.config.annotation.WebMvcConfigurer;
@Configuration
public class MyWebMvcConfig implements WebMvcConfigurer {@Overridepublic void addCorsMappings(CorsRegistry registry) {registry.addMapping("/**") // 所有接口.allowCredentials(true) // 是否发送 Cookie.allowedOriginPatterns("*") // 支持域.allowedMethods("*") .allowedHeaders("*").exposedHeaders("*");}
}
php
header("Access-Control-Allow-Origin: *"); // 允许所有地址跨域
thinkphp6
// 在/app/middleware.php中加入以下代码
\think\middleware\AllowCrossDomain::class
以上如果已配置完成还报错,可以试着参考以下方式
前端axios请求地址如果为’http://localhost:8080/',在浏览器地址中访问也换成localhost