如果用局域网做网站网页设计是什么岗位
文章目录
- 【`获取资源`请见文章第5节:资源获取】
- 1. 原始POA算法
- 2. 改进后的IPOA算法
- 2.1 Sine映射种群初始化
- 2.2 融合改进的正余弦策略
- 2.3 Levy飞行策略
- 3. 部分代码展示
- 4. 仿真结果展示
- 5. 资源获取
【获取资源请见文章第5节:资源获取】
1. 原始POA算法
此算法详细介绍请参考POA算法介绍
2. 改进后的IPOA算法
2.1 Sine映射种群初始化
混沌映射可以使种群在搜索空间中的分布更加均匀,因此被广泛使用。其中,Sine映射是一种不错的映射方式,其数学表达式为:
x n + 1 = a 4 s i n ( π ∗ x n ) (1) x_{n+1}=\frac{a}{4}sin(\pi*x_{n})\tag1 xn+1=4asin(π∗xn)(1)
2.2 融合改进的正余弦策略
正余弦优化算法利用正余弦函数的周期性波动构造迭代方程,实现全局搜索和局部开发两个阶段的功能。具体的迭代方程分为以下两类正弦迭代或迭代余弦方程:
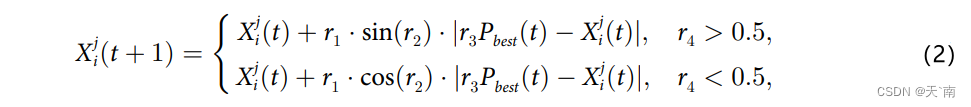
其中, t t t为当前迭代次数, X i j ( t ) X_{i}^{j}(t) Xij(t)表示第 t t t次迭代时第 i i i个个体的第 j j j维变量, r 1 r_{1} r1和 r 3 r_{3} r3表示[0,1]之间的随机数, r 2 r_{2} r2表示[0,2π]之间的随机数, P b e s t ( t ) P_{best}(t) Pbest(t)表示第 t t t次迭代的最优解。
为了进一步提高POA算法的全局开发能力,在引入了正余弦策略的基础上,还加入了鲸鱼优化算法的螺旋更新策略。
2.3 Levy飞行策略
在原始POA算法的探索阶段,容易陷入局部最优,为了提高跳出局部最优的能力,可以使用莱维飞行策略进行位置更新使得这部分鹈鹕个体去到更广的搜索空间:

3. 部分代码展示
%%
clc
clear
close all%%
Fun_name='F1'; % number of test functions: 'F1' to 'F23'
SearchAgents=30; % number of Pelicans (population members)
Max_iterations=500; % maximum number of iteration
[lb,ub,dim,fobj]=Get_Functions_details(Fun_name); % Object function information
[Best_score_POA,Best_pos_POA,POA_curve]=POA(SearchAgents,Max_iterations,lb,ub,dim,fobj);
[Best_score_SSA,Best_pos_SSA,SSA_curve]=SSA(SearchAgents,Max_iterations,lb,ub,dim,fobj);
[Best_score_WOA,Best_pos_WOA,WOA_curve]=WOA(SearchAgents,Max_iterations,lb,ub,dim,fobj);
[Best_score_GWO,Best_pos_GWO,GWO_curve]=GWO(SearchAgents,Max_iterations,lb,ub,dim,fobj);
[Best_score_IPOA,Best_pos_IPOA,IPOA_curve]=IPOA(SearchAgents,Max_iterations,lb,ub,dim,fobj);%%
figure('Position',[454 445 694 297]);
subplot(1,2,1);
func_plot(Fun_name);
title('Parameter space')
xlabel('x_1');
ylabel('x_2');
zlabel([Fun_name,'( x_1 , x_2 )'])subplot(1,2,2);
t = 1:Max_iterations;
semilogy(t, POA_curve, 'b-', t, SSA_curve, 'k-', t, WOA_curve, 'g-', t, GWO_curve, 'm-', t, IPOA_curve, 'r-','linewidth', 1.5);title(Fun_name)
xlabel('Iteration');
ylabel('Best fitness function');
axis tight
legend('POA','SSA','WOA','GWO','IPOA')display(['The best solution obtained by POA for ' [num2str(Fun_name)],' is : ', num2str(Best_pos_POA)]);
display(['The best optimal value of the objective funciton found by POA for ' [num2str(Fun_name)],' is : ', num2str(Best_score_POA)]);
display(['The best solution obtained by SSA for ' [num2str(Fun_name)],' is : ', num2str(Best_pos_SSA)]);
display(['The best optimal value of the objective funciton found by SSA for ' [num2str(Fun_name)],' is : ', num2str(Best_score_SSA)]);
display(['The best solution obtained by WOA for ' [num2str(Fun_name)],' is : ', num2str(Best_pos_WOA)]);
display(['The best optimal value of the objective funciton found by WOA for ' [num2str(Fun_name)],' is : ', num2str(Best_score_WOA)]);
display(['The best solution obtained by GWO for ' [num2str(Fun_name)],' is : ', num2str(Best_pos_GWO)]);
display(['The best optimal value of the objective funciton found by GWO for ' [num2str(Fun_name)],' is : ', num2str(Best_score_GWO)]);
display(['The best solution obtained by IPOA for ' [num2str(Fun_name)],' is : ', num2str(Best_pos_IPOA)]);
display(['The best optimal value of the objective funciton found by IPOA for ' [num2str(Fun_name)],' is : ', num2str(Best_score_IPOA)]);
4. 仿真结果展示








5. 资源获取
可以获取完整代码资源。
