做网站的属于什么专业?深圳市住建局官网入口
Spring知识快速复习
- 启动器
- 自动装配
- @Configuration
- @Import导入组件
- @Conditional条件装配
- @ImportResource导入Spring配置文件
- @ConfigurationProperties配置绑定
- Lombok简化开发
- dev-tools
- yaml
- 请求和响应处理
- 静态资源规则与定制化
- 请求处理-Rest映射
- 请求处理-常用参数注解使用
- 请求处理-Servlet API参数
- 请求处理-Model、Map
- 请求处理-自定义Converter
- 响应处理-ReturnValueHandler
- 响应处理-内容协商
- 响应处理-基于请求参数的内容协商
- 响应处理-自定义MessageConverter
- Web开发
- 视图解析--视图解析器与视图
- 拦截器-登录检查与静态资源放行
- 拦截器-拦截器的执行时机和原理
- 文件上传-单文件与多文件上传的使用
- 文件上传-文件上传参数解析器
- 错误处理-SpringBoot默认错误处理机制
- 原生组件注入-原生注解与Spring方式注入
- 定制化springmvc
- 原理分析套路
- 数据访问
- JDBC
- Druid
- MyBatis
- MyBatisPlus
- 添加分页插件
- Redis
- JUnit5
- 常用测试注解
- 断言机制
- 前置条件
- 嵌套测试
- 参数化测试
- 迁移指南
- 指标监控
- Actuator
- 常使用的端点及开启与禁用
- 常使用的端点
- Health Endpoint
- Metrics Endpoint
- 开启与禁用Endpoints
- 暴露Endpoints
- 定制Endpoint
- 定制 Health 信息
- 定制info信息
- 定制Metrics信息
- 定制Endpoint
- 自定义starter
- starter启动原理
- 自定义starter
- SpringBoot完整启动过程
启动器
spring-boot-starter-* : 官方提供的
*-spring-boot-starter : 第三方提供的
自动装配
@Configuration
告诉SpringBoot这是一个配置类
1、配置类里面使用@Bean标注在方法上给容器注册组件,默认也是单实例的
2、配置类本身也是组件
使用代理,容器实例唯一,不使用代理,多次调用多个实例
3、proxyBeanMethods:代理bean的方法
- Full(proxyBeanMethods = true)(保证每个@Bean方法被调用多少次返回的组件都是单实例的)(默认)
- Lite(proxyBeanMethods = false)(每个@Bean方法被调用多少次返回的组件都是新创建的)
最佳实战
- 配置 类组件之间无依赖关系用Lite模式加速容器启动过程,减少判断,设置为false
- 配置 类组件之间有依赖关系,方法会被调用得到之前单实例组件,用Full模式(默认),设置为true
@Import导入组件
@Bean、@Component、@Controller、@Service、@Repository,它们是Spring的基本标签,在Spring Boot中并未改变它们原来的功能。
@Import({User.class, DBHelper.class})给容器中自动创建出这两个类型的组件、默认组件的名字就是全类名
@Conditional条件装配
@ConditionalOnMissingBean 如果容器中没有配置这个对象,就会配置该对象
条件装配:满足Conditional指定的条件,则进行组件注入
@ImportResource导入Spring配置文件
想继续复用bean.xml,使用@ImportResource
@ConfigurationProperties配置绑定
使用Java读取到properties文件中的内容,并且把它封装到JavaBean中,以供随时使用
- Spring Boot一种配置配置绑定:
@ConfigurationProperties + @Component
- Spring Boot另一种配置配置绑定(第三方包无法添加@Component注解):
@EnableConfigurationProperties + @ConfigurationProperties
对于单个值,使用@Value
使用@Value注解
@Value(“${属性值:默认值}”)
Lombok简化开发
Lombok用标签方式代替构造器、getter/setter、toString()等鸡肋代码。
@NoArgsConstructor //无参构造器
@AllArgsConstructor //全参构造器
@Data //生成已有属性的getter和setter方法
@ToString //生成tostring方法
@EqualsAndHashCode //重写equals和hashcode
dev-tools
在IDEA中,项目或者页面修改以后:Ctrl+F9。
yaml
用来做以数据为中心的配置文件
@ConfigurationProperties配置后 properties最高,yml其次,yaml最低
请求和响应处理
静态资源规则与定制化
只要静态资源放在类路径下: called /static (or /public or /resources or /META-INF/resources
改变默认的静态资源路径
web:resources:static-locations: [classpath:/haha/]
静态资源访问前缀
spring:mvc:static-path-pattern: /res/**
当前项目 + static-path-pattern + 静态资源名 = 静态资源文件夹下找
请求处理-Rest映射
@xxxMapping;
- @GetMapping
- @PostMapping
- @PutMapping
- @DeleteMapping
用法
- 开启页面表单的Rest功能
- 页面 form的属性method=post,隐藏域 _method=put、delete等(如果直接get或post,无需隐藏域)
- 编写请求映射
spring:mvc:hiddenmethod:filter:enabled: true #开启页面表单的Rest功能
Rest原理(表单提交要使用REST的时候)
- 表单提交会带上
\_method=PUT - 请求过来被
HiddenHttpMethodFilter拦截- 请求是否正常,并且是POST
- 获取到
\_method的值。 - 兼容以下请求;PUT.DELETE.PATCH
- 原生request(post),包装模式requesWrapper重写了getMethod方法,返回的是传入的值。
- 过滤器链放行的时候用wrapper。以后的方法调用getMethod是调用requesWrapper的。
- 获取到
- 请求是否正常,并且是POST
请求处理-常用参数注解使用
@PathVariable路径变量 。@PathVariable Map<String,String> pv 就会将所有路径变量数据放入pv中@RequestHeader获取请求头@RequestParam获取请求参数(指问号后的参数,url?a=1&b=2)@CookieValue获取Cookie值@RequestAttribute获取request域属性@RequestBody获取请求体[POST]@MatrixVariable矩阵变量@ModelAttribute
矩阵变量-@MatrixVariable
语法: 请求路径:/cars/sell;low=34;brand=byd,audi,yd
原理:
HandlerMapping中找到能处理请求的Handler(Controller.method())。- 为当前Handler 找一个适配器
HandlerAdapter,用的最多的是RequestMappingHandlerAdapter。 - 适配器执行目标方法并确定方法参数的每一个值。
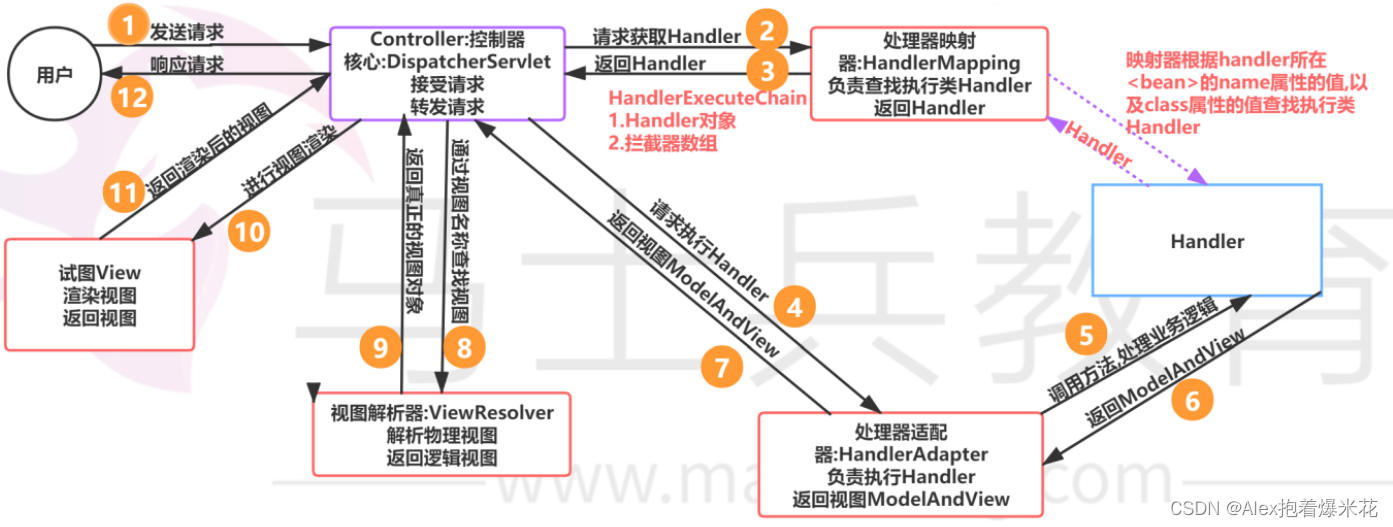
将确定每个方法参数的值的过程封装到HandlerAdapter里面,相当于大的反射工具
请求处理-Servlet API参数
- WebRequest
- ServletRequest
- MultipartRequest
- HttpSession
- javax.servlet.http.PushBuilder
- Principal
- InputStream
- Reader
- HttpMethod
- Locale
- TimeZone
- ZoneId
请求处理-Model、Map
复杂参数:
- Map
- Model(map、model里面的数据会被放在request的请求域 request.setAttribute)
- Errors/BindingResult
- RedirectAttributes( 重定向携带数据)
- ServletResponse(response)
- SessionStatus
- UriComponentsBuilder
- ServletUriComponentsBuilder
model和map放到请求域中是在渲染之前进行的
请求处理-自定义Converter
未来我们可以给WebDataBinder里面放自己的Converter;
下面演示将字符串“啊猫,3”转换成Pet对象。
//1、WebMvcConfigurer定制化SpringMVC的功能@Beanpublic WebMvcConfigurer webMvcConfigurer(){return new WebMvcConfigurer() {@Overridepublic void addFormatters(FormatterRegistry registry) {registry.addConverter(new Converter<String, Pet>() {@Overridepublic Pet convert(String source) {// 啊猫,3if(!StringUtils.isEmpty(source)){Pet pet = new Pet();String[] split = source.split(",");pet.setName(split[0]);pet.setAge(Integer.parseInt(split[1]));return pet;}return null;}});}};}
响应处理-ReturnValueHandler
@ResponseBody 注解,即RequestResponseBodyMethodProcessor,它实现HandlerMethodReturnValueHandler接口
返回值处理器ReturnValueHandler原理:
- 返回值处理器判断是否支持这种类型返回值
supportsReturnType - 返回值处理器调用
handleReturnValue进行处理 RequestResponseBodyMethodProcessor可以处理返回值标了@ResponseBody注解的。- 利用
MessageConverters进行处理 将数据写为json- 内容协商(浏览器默认会以请求头的方式告诉服务器他能接受什么样的内容类型)
- 服务器最终根据自己自身的能力,决定服务器能生产出什么样内容类型的数据,
- SpringMVC会挨个遍历所有容器底层的
HttpMessageConverter,看谁能处理?- 得到
MappingJackson2HttpMessageConverter可以将对象写为json - 利用
MappingJackson2HttpMessageConverter将对象转为json再写出去。
- 得到
- 利用
HttpMessageConverter: 看是否支持将 此 Class类型的对象,转为MediaType类型的数据。
例子:Person对象转为JSON,或者 JSON转为Person,这将用到MappingJackson2HttpMessageConverter
响应处理-内容协商
根据客户端接收能力不同,返回不同媒体类型的数据。Http协议中规定的,Accept字段告诉服务器本客户端可以接收的数据类型。
内容协商原理:
- 判断当前响应头中是否已经有确定的媒体类型
MediaType。 - 获取客户端(PostMan、浏览器)支持接收的内容类型。(获取客户端Accept请求头字段application/xml)getAcceptableMediaTypes 中
contentNegotiationManager内容协商管理器 默认使用基于请求头的策略HeaderContentNegotiationStrategy确定客户端可以接收的内容类型
- 遍历循环所有当前系统的
MessageConverter,看谁支持操作这个对象(Person) - 找到支持操作Person的converter,把converter支持的媒体类型统计出来。
- 客户端需要application/xml,服务端有10种MediaType。
- 进行内容协商的最佳匹配媒体类型
- 用 支持 将对象转为 最佳匹配媒体类型 的converter。调用它进行转化 。
响应处理-基于请求参数的内容协商
上面内容协商的第二步
获取客户端(PostMan、浏览器)支持接收的内容类型。(获取客户端Accept请求头字段application/xml)getAcceptableMediaTypes 中
contentNegotiationManager内容协商管理器 默认使用基于请求头的策略HeaderContentNegotiationStrategy确定客户端可以接收的内容类型
spring:mvc:contentnegotiation:favor-parameter: true #开启请求参数内容协商模式
开启基于请求参数的内容协商功能。内容协商管理器,就会多了一个ParameterContentNegotiationStrategy(由Spring容器注入)然后,浏览器地址输入带format参数的URL:
http://localhost:8080/test/person?format=json
或
http://localhost:8080/test/person?format=xml
这样,后端会根据参数format的值,返回对应json或xml格式的数据。
响应处理-自定义MessageConverter
实现多协议数据兼容。json、xml、x-guigu(这个是自创的)
-
@ResponseBody响应数据出去 调用RequestResponseBodyMethodProcessor处理 -
Processor 处理方法返回值。通过
MessageConverter处理 -
所有
MessageConverter合起来可以支持各种媒体类型数据的操作(读、写) -
内容协商找到最终的
messageConverter
SpringMVC的什么功能,一个入口给容器中添加一个 WebMvcConfigurer
@Configuration(proxyBeanMethods = false)
public class WebConfig {@Beanpublic WebMvcConfigurer webMvcConfigurer(){return new WebMvcConfigurer() {@Overridepublic void extendMessageConverters(List<HttpMessageConverter<?>> converters) {converters.add(new GuiguMessageConverter());}}}
}
Web开发
视图解析–视图解析器与视图
视图解析原理流程:
-
目标方法处理的过程中(阅读
DispatcherServlet源码),所有数据都会被放在ModelAndViewContainer里面,其中包括数据和视图地址。 -
方法的参数是一个自定义类型对象(从请求参数中确定的),把他重新放在
ModelAndViewContainer。 -
任何目标方法执行完成以后都会返回
ModelAndView(数据和视图地址)。 -
processDispatchResult()处理派发结果(页面改如何响应)-
render(mv, request, response);进行页面渲染逻辑- 根据方法的
String返回值得到View对象【定义了页面的渲染逻辑】
- 所有的视图解析器尝试是否能根据当前返回值得到
View对象 - 得到了
redirect:/main.html --> Thymeleaf new RedirectView()。 ContentNegotiationViewResolver里面包含了下面所有的视图解析器,内部还是利用下面所有视图解析器得到视图对象。view.render(mv.getModelInternal(), request, response);视图对象调用自定义的render进行页面渲染工作。
RedirectView如何渲染【重定向到一个页面】- 获取目标url地址
response.sendRedirect(encodedURL);
- 根据方法的
-
视图解析:
- 返回值以 forward: 开始: new InternalResourceView(forwardUrl); --> 转发request.getRequestDispatcher(path).forward(request, response);
- 返回值以 redirect: 开始: new RedirectView() --> render就是重定向
- 返回值是普通字符串:new ThymeleafView()—>
拦截器-登录检查与静态资源放行
Filter、Interceptor的区别?
- Filter是Servlet定义的原生组件,它的好处是脱离Spring应用也能使用。
- Interceptor是Spring定义的接口,可以使用Spring的自动装配等功能。
-
编写一个拦截器实现
HandlerInterceptor接口 -
拦截器注册到容器中(实现
WebMvcConfigurer的addInterceptors()) -
指定拦截规则(注意,如果是拦截所有,静态资源也会被拦截】
@Slf4j
public class LoginInterceptor implements HandlerInterceptor {/*** 目标方法执行之前*/@Overridepublic boolean preHandle(HttpServletRequest request, HttpServletResponse response, Object handler) throws Exception {String requestURI = request.getRequestURI();log.info("preHandle拦截的请求路径是{}",requestURI);//登录检查逻辑HttpSession session = request.getSession();Object loginUser = session.getAttribute("loginUser");if(loginUser != null){//放行return true;}//拦截住。未登录。跳转到登录页request.setAttribute("msg","请先登录");
// re.sendRedirect("/");request.getRequestDispatcher("/").forward(request,response);return false;}/*** 目标方法执行完成以后*/@Overridepublic void postHandle(HttpServletRequest request, HttpServletResponse response, Object handler, ModelAndView modelAndView) throws Exception {log.info("postHandle执行{}",modelAndView);}/*** 页面渲染以后*/@Overridepublic void afterCompletion(HttpServletRequest request, HttpServletResponse response, Object handler, Exception ex) throws Exception {log.info("afterCompletion执行异常{}",ex);}
}
拦截器注册到容器中 && 指定拦截规则:
@Configuration
public class AdminWebConfig implements WebMvcConfigurer{@Overridepublic void addInterceptors(InterceptorRegistry registry) {registry.addInterceptor(new LoginInterceptor())//拦截器注册到容器中.addPathPatterns("/**") //所有请求都被拦截包括静态资源.excludePathPatterns("/","/login","/css/**","/fonts/**","/images/**","/js/**","/aa/**"); //放行的请求
}
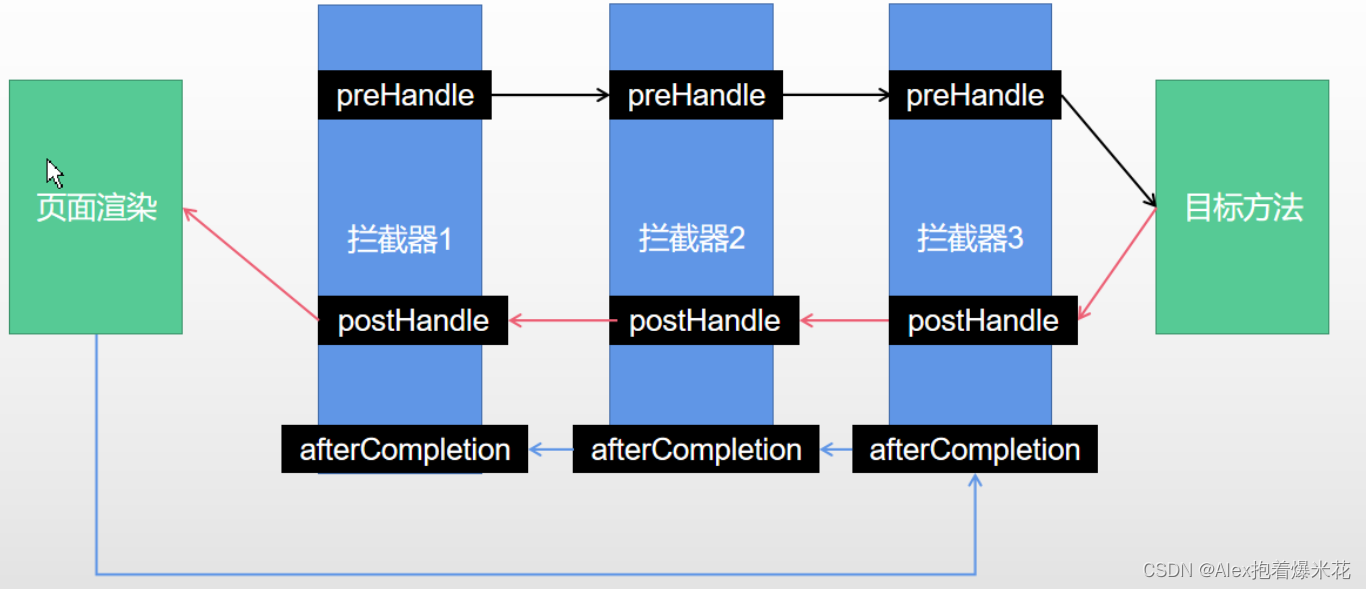
拦截器-拦截器的执行时机和原理
- 根据当前请求,找到
HandlerExecutionChain(可以处理请求的handler以及handler的所有 拦截器) - 先来顺序执行 所有拦截器的
preHandle()方法。- 如果当前拦截器
preHandle()返回为true。则执行下一个拦截器的preHandle() - 如果当前拦截器返回为
false。直接倒序执行所有已经执行了的拦截器的afterCompletion();。
- 如果当前拦截器
- 如果任何一个拦截器返回
false,直接跳出不执行目标方法。 - 所有拦截器都返回
true,才执行目标方法。 - 倒序执行所有拦截器的
postHandle()方法。 - 前面的步骤有任何异常都会直接倒序触发
afterCompletion()。 - 页面成功渲染完成以后,也会倒序触发
afterCompletion()。
文件上传-单文件与多文件上传的使用
@RequestPart注解 + MultipartFile 类型
文件大小相关配置项
spring.servlet.multipart.max-file-size=10MB
spring.servlet.multipart.max-request-size=100MB
@Slf4j
@Controller
public class FormTestController {@GetMapping("/form_layouts")public String form_layouts(){return "form/form_layouts";}@PostMapping("/upload")public String upload(@RequestParam("email") String email,@RequestParam("username") String username,@RequestPart("headerImg") MultipartFile headerImg,@RequestPart("photos") MultipartFile[] photos) throws IOException {log.info("上传的信息:email={},username={},headerImg={},photos={}",email,username,headerImg.getSize(),photos.length);if(!headerImg.isEmpty()){//保存到文件服务器,OSS服务器String originalFilename = headerImg.getOriginalFilename();headerImg.transferTo(new File("H:\\cache\\"+originalFilename));}if(photos.length > 0){for (MultipartFile photo : photos) {if(!photo.isEmpty()){String originalFilename = photo.getOriginalFilename();photo.transferTo(new File("H:\\cache\\"+originalFilename));}}}return "main";}
}
文件上传-文件上传参数解析器
文件上传相关的自动配置类MultipartAutoConfiguration有创建文件上传参数解析器StandardServletMultipartResolver。
文件上传自动配置类—MultipartAutoConfiguration—MultipartProperties;自动配置好了 StandardServletMultipartResolver 【文件上传解析器】
原理步骤
- 请求进来使用文件上传解析器判断(isMultipart)并封装(resolveMultipart,返回MultipartHttpServletRequest)文件上传请求
- 参数解析器来解析请求中的文件内容封装成MultipartFile
- 将request中文件信息封装为一个Map;MultiValueMap<String, MultipartFile>。 FileCopyUtils,实现文件流的拷贝
错误处理-SpringBoot默认错误处理机制
默认规则:
-
默认情况下,Spring Boot提供
/error处理所有错误的映射 -
机器客户端,它将生成JSON响应,其中包含错误,HTTP状态和异常消息的详细信息。对于浏览器客户端,响应一个“ whitelabel”错误视图,以HTML格式呈现相同的数据
定制错误处理逻辑
-
自定义错误页
error/404.html error/5xx.html;有精确的错误状态码页面就匹配精确,没有就找 4xx.html;如果都没有就触发白页 -
@ControllerAdvice+@ExceptionHandler处理全局异常;底层是
ExceptionHandlerExceptionResolver支持的@Slf4j @ControllerAdvice public class GlobalExceptionHandler {@ExceptionHandler({ArithmeticException.class,NullPointerException.class}) //处理异常public String handleArithException(Exception e){log.error("异常是:{}",e);return "login"; //视图地址} } -
@ResponseStatus+自定义异常 ;底层是
ResponseStatusExceptionResolver,把responseStatus注解的信息底层调用response.sendError(statusCode, resolvedReason),tomcat发送的/error@ResponseStatus(value= HttpStatus.FORBIDDEN,reason = "用户数量太多") public class UserTooManyException extends RuntimeException {public UserTooManyException(){}public UserTooManyException(String message){super(message);} }@Controller public class TableController {@GetMapping("/dynamic_table")public String dynamic_table(@RequestParam(value="pn",defaultValue = "1") Integer pn,Model model){//表格内容的遍历List<User> users = Arrays.asList(new User("zhangsan", "123456"),new User("lisi", "123444"),new User("haha", "aaaaa"),new User("hehe ", "aaddd"));model.addAttribute("users",users);if(users.size()>3){throw new UserTooManyException();//抛出自定义异常}return "table/dynamic_table";}} -
Spring底层的异常,如 参数类型转换异常;
DefaultHandlerExceptionResolver处理框架底层的异常
response.sendError(HttpServletResponse.SC_BAD_REQUEST, ex.getMessage()); -
自定义实现
HandlerExceptionResolver处理异常;可以作为默认的全局异常处理规则@Order(value= Ordered.HIGHEST_PRECEDENCE) //优先级,数字越小优先级越高 @Component public class CustomerHandlerExceptionResolver implements HandlerExceptionResolver {@Overridepublic ModelAndView resolveException(HttpServletRequest request,HttpServletResponse response,Object handler, Exception ex) {try {response.sendError(511,"我喜欢的错误");} catch (IOException e) {e.printStackTrace();}return new ModelAndView();} }
异常处理自动配置原理
ErrorMvcAutoConfiguration自动配置异常处理规则- 容器中的组件:类型:
DefaultErrorAttributes-> id:errorAttributes public class DefaultErrorAttributes implements ErrorAttributes, HandlerExceptionResolverDefaultErrorAttributes:定义错误页面中可以包含数据(异常明细,堆栈信息等)。
- 容器中的组件:类型:
BasicErrorController--> id:basicErrorController(json+白页 适配响应) - 处理默认
/error路径的请求,页面响应new ModelAndView("error", model);- 容器中有组件
View->id是error;(响应默认错误页) - 容器中放组件
BeanNameViewResolver(视图解析器);按照返回的视图名作为组件的id去容器中找View对象。
- 容器中有组件
- 容器中的组件:类型:
DefaultErrorViewResolver-> id:conventionErrorViewResolver - 如果发生异常错误,会以HTTP的状态码 作为视图页地址(viewName),找到真正的页面(主要作用)。
- error/404、5xx.html
- 如果想要返回页面,就会找error视图(
StaticView默认是一个白页)。
总结:如果想要返回页面;就会找error视图【StaticView】。(默认是一个白页)
要么响应一个modelandvie(页面),要么响应一个responseentity(json)
原生组件注入-原生注解与Spring方式注入
使用原生的注解
1、添加@WebServlet(urlPatterns = “/my”)注解 ; @WebFilter(urlPatterns={“/css/“,”/images/”}) ;@WebListener
2、在主启动类添加注解@ServletComponentScan指定原生Servlet组件都放在那里
@WebServlet(urlPatterns = "/my")
public class MyServlet extends HttpServlet {@Overrideprotected void doGet(HttpServletRequest req, HttpServletResponse resp) throws ServletException, IOException {resp.getWriter().write("66666");}
}
@Slf4j
@WebFilter(urlPatterns={"/css/*","/images/*"}) //my
public class MyFilter implements Filter {@Overridepublic void init(FilterConfig filterConfig) throws ServletException {log.info("MyFilter初始化完成");}@Overridepublic void doFilter(ServletRequest request, ServletResponse response, FilterChain chain) throws IOException, ServletException {log.info("MyFilter工作");chain.doFilter(request,response);}@Overridepublic void destroy() {log.info("MyFilter销毁");}
}
@Slf4j
@WebListener
public class MyServletContextListener implements ServletContextListener {@Overridepublic void contextInitialized(ServletContextEvent sce) {log.info("MySwervletContextListener监听到项目初始化完成");}@Overridepublic void contextDestroyed(ServletContextEvent sce) {log.info("MySwervletContextListener监听到项目销毁");}
}
最后还要在主启动类添加注解@ServletComponentScan
@ServletComponentScan(basePackages = "com.lun")//
@SpringBootApplication(exclude = RedisAutoConfiguration.class)
public class Boot05WebAdminApplication {public static void main(String[] args) {SpringApplication.run(Boot05WebAdminApplication.class, args);}
}
定制化springmvc
@EnableWebMvc+WebMvcConfigurer—@Bean可以全面接管SpringMVC,所有规则全部自己重新配置; 实现定制和扩展功能(高级功能,初学者退避三舍)。- 原理:
WebMvcAutoConfiguration默认的SpringMVC的自动配置功能类,如静态资源、欢迎页等。- 一旦使用
@EnableWebMvc,会@Import(DelegatingWebMvcConfiguration.class)。 DelegatingWebMvcConfiguration的作用,只保证SpringMVC最基本的使用- 把所有系统中的
WebMvcConfigurer拿过来,所有功能的定制都是这些WebMvcConfigurer合起来一起生效。 - 自动配置了一些非常底层的组件,如
RequestMappingHandlerMapping,这些组件依赖的组件都是从容器中获取如。 public class DelegatingWebMvcConfiguration extends WebMvcConfigurationSupport。
- 把所有系统中的
WebMvcAutoConfiguration里面的配置要能生效必须@ConditionalOnMissingBean(WebMvcConfigurationSupport.class)。- @EnableWebMvc 导致了WebMvcAutoConfiguration 没有生效。
- 原理:
原理分析套路
场景starter - xxxxAutoConfiguration - 导入xxx组件 - 绑定xxxProperties - 绑定配置文件项。
数据访问
JDBC
spring:datasource:url: jdbc:mysql://localhost:3306/db_accountusername: rootpassword: 123456driver-class-name: com.mysql.jdbc.Driver
Druid
数据库连接池,它能够提供强大的监控和扩展功能。
spring:datasource:url: jdbc:mysql://localhost:3306/db_accountusername: rootpassword: 123456driver-class-name: com.mysql.jdbc.Driverdruid:aop-patterns: com.atguigu.admin.* #监控SpringBeanfilters: stat,wall # 底层开启功能,stat(sql监控),wall(防火墙)stat-view-servlet: # 配置监控页功能enabled: truelogin-username: adminlogin-password: adminresetEnable: falseweb-stat-filter: # 监控webenabled: trueurlPattern: /*exclusions: '*.js,*.gif,*.jpg,*.png,*.css,*.ico,/druid/*'filter:stat: # 对上面filters里面的stat的详细配置slow-sql-millis: 1000logSlowSql: trueenabled: truewall:enabled: trueconfig:drop-table-allow: false
MyBatis
spring:datasource:username: rootpassword: 1234url: jdbc:mysql://localhost:3306/mydriver-class-name: com.mysql.jdbc.Driver# 配置mybatis规则
mybatis:config-location: classpath:mybatis/mybatis-config.xml #全局配置文件位置mapper-locations: classpath:mybatis/*.xml #sql映射文件位置
mybatis-config.xml:
<?xml version="1.0" encoding="UTF-8" ?>
<!DOCTYPE configurationPUBLIC "-//mybatis.org//DTD Config 3.0//EN""http://mybatis.org/dtd/mybatis-3-config.dtd">
<configuration><!-- 由于Spring Boot自动配置缘故,此处不必配置,只用来做做样。-->
</configuration>
注解与配置混合搭配,干活不累:
@Mapper
public interface UserMapper {public User getUser(Integer id);@Select("select * from user where id=#{id}")public User getUser2(Integer id);public void saveUser(User user);@Insert("insert into user(`name`) values(#{name})")@Options(useGeneratedKeys = true, keyProperty = "id")public void saveUser2(User user);}<?xml version="1.0" encoding="UTF-8" ?>
<!DOCTYPE mapperPUBLIC "-//mybatis.org//DTD Mapper 3.0//EN""http://mybatis.org/dtd/mybatis-3-mapper.dtd">
<mapper namespace="com.lun.boot.mapper.UserMapper"><select id="getUser" resultType="com.lun.boot.bean.User">select * from user where id=#{id}</select><insert id="saveUser" useGeneratedKeys="true" keyProperty="id">insert into user(`name`) values(#{name})</insert></mapper>
简单DAO方法就写在注解上。复杂的就写在配置文件里。
使用@MapperScan("com.lun.boot.mapper") 简化,Mapper接口就可以不用标注@Mapper注解。
小结
- 导入mybatis-starter。
- 编写Mapper接口,需
@Mapper注解。 - 编写SQL映射文件并绑定Mapper接口。
- 在
application.yaml中指定Mapper配置文件的所处位置mapper-location,以及指定全局配置文件的信息 (建议:配置在mybatis.configuration)。 - 在启动程序Application上添加@MapperScan(“com.atguigu.admin.mapper”) 简化,其他的接口就可以不用标注@Mapper注解
MyBatisPlus
import com.baomidou.mybatisplus.core.mapper.BaseMapper;
import com.lun.hellomybatisplus.model.User;public interface UserMapper extends BaseMapper<User> {}
/*** Service 的CRUD也不用写了*/
public interface UserService extends IService<User> {//此处故意为空
}
@Service
public class UserServiceImpl extends ServiceImpl<UserMapper,User> implements UserService {//此处故意为空
}
添加分页插件
@Configuration
public class MyBatisConfig {/*** MybatisPlusInterceptor* @return*/@Beanpublic MybatisPlusInterceptor paginationInterceptor() {MybatisPlusInterceptor mybatisPlusInterceptor = new MybatisPlusInterceptor();// 设置请求的页面大于最大页后操作, true调回到首页,false 继续请求 默认false// paginationInterceptor.setOverflow(false);// 设置最大单页限制数量,默认 500 条,-1 不受限制// paginationInterceptor.setLimit(500);// 开启 count 的 join 优化,只针对部分 left join//这是分页拦截器PaginationInnerInterceptor paginationInnerInterceptor = new PaginationInnerInterceptor();paginationInnerInterceptor.setOverflow(true);paginationInnerInterceptor.setMaxLimit(500L);mybatisPlusInterceptor.addInnerInterceptor(paginationInnerInterceptor);return mybatisPlusInterceptor;}
}
Redis
spring:redis:
# url: redis://lfy:Lfy123456@r-bp1nc7reqesxisgxpipd.redis.rds.aliyuncs.com:6379host: r-bp1nc7reqesxisgxpipd.redis.rds.aliyuncs.comport: 6379password: lfy:Lfy123456client-type: jedisjedis:pool:max-active: 10
# lettuce:# 另一个用来连接redis的java框架
# pool:
# max-active: 10
# min-idle: 5
URL统计拦截器:
@Component
public class RedisUrlCountInterceptor implements HandlerInterceptor {@AutowiredStringRedisTemplate redisTemplate;@Overridepublic boolean preHandle(HttpServletRequest request, HttpServletResponse response, Object handler) throws Exception {String uri = request.getRequestURI();//默认每次访问当前uri就会计数+1redisTemplate.opsForValue().increment(uri);return true;}
}
注册URL统计拦截器:
@Configuration
public class AdminWebConfig implements WebMvcConfigurer{@AutowiredRedisUrlCountInterceptor redisUrlCountInterceptor;@Overridepublic void addInterceptors(InterceptorRegistry registry) {registry.addInterceptor(redisUrlCountInterceptor).addPathPatterns("/**").excludePathPatterns("/","/login","/css/**","/fonts/**","/images/**","/js/**","/aa/**");}
}
Filter、Interceptor的区别?
- Filter是Servlet定义的原生组件,它的好处是脱离Spring应用也能使用。
- Interceptor是Spring定义的接口,可以使用Spring的自动装配等功能。
JUnit5
常用测试注解
- @Test:表示方法是测试方法。但是与JUnit4的@Test不同,他的职责非常单一不能声明任何属性,拓展的测试将会由Jupiter提供额外测试
- @ParameterizedTest:表示方法是参数化测试。
- @RepeatedTest:表示方法可重复执行。
- @DisplayName:为测试类或者测试方法设置展示名称。
- @BeforeEach:表示在每个单元测试之前执行。
- @AfterEach:表示在每个单元测试之后执行。
- @BeforeAll:表示在所有单元测试之前执行。
- @AfterAll:表示在所有单元测试之后执行。
- @Tag:表示单元测试类别,类似于JUnit4中的@Categories。
- @Disabled:表示测试类或测试方法不执行,类似于JUnit4中的@Ignore。
- @Timeout:表示测试方法运行如果超过了指定时间将会返回错误。
- @ExtendWith:为测试类或测试方法提供扩展类引用。
import org.junit.jupiter.api.*;@DisplayName("junit5功能测试类")
public class Junit5Test {@DisplayName("测试displayname注解")@Testvoid testDisplayName() {System.out.println(1);System.out.println(jdbcTemplate);}@ParameterizedTest@ValueSource(strings = { "racecar", "radar", "able was I ere I saw elba" })void palindromes(String candidate) {assertTrue(StringUtils.isPalindrome(candidate));}@Disabled@DisplayName("测试方法2")@Testvoid test2() {System.out.println(2);}@RepeatedTest(5)@Testvoid test3() {System.out.println(5);}/*** 规定方法超时时间。超出时间测试出异常** @throws InterruptedException*/@Timeout(value = 500, unit = TimeUnit.MILLISECONDS)@Testvoid testTimeout() throws InterruptedException {Thread.sleep(600);}@BeforeEachvoid testBeforeEach() {System.out.println("测试就要开始了...");}@AfterEachvoid testAfterEach() {System.out.println("测试结束了...");}@BeforeAllstatic void testBeforeAll() {System.out.println("所有测试就要开始了...");}@AfterAllstatic void testAfterAll() {System.out.println("所有测试以及结束了...");}}
断言机制
- 简单断言
| 方法 | 说明 |
|---|---|
| assertEquals | 判断两个对象或两个原始类型是否相等 |
| assertNotEquals | 判断两个对象或两个原始类型是否不相等 |
| assertSame | 判断两个对象引用是否指向同一个对象 |
| assertNotSame | 判断两个对象引用是否指向不同的对象 |
| assertTrue | 判断给定的布尔值是否为 true |
| assertFalse | 判断给定的布尔值是否为 false |
| assertNull | 判断给定的对象引用是否为 null |
| assertNotNull | 判断给定的对象引用是否不为 null |
@Test
@DisplayName("simple assertion")
public void simple() {assertEquals(3, 1 + 2, "simple math");assertNotEquals(3, 1 + 1);assertNotSame(new Object(), new Object());Object obj = new Object();assertSame(obj, obj);assertFalse(1 > 2);assertTrue(1 < 2);assertNull(null);assertNotNull(new Object());
}
- 数组断言
通过 assertArrayEquals 方法来判断两个对象或原始类型的数组是否相等。
@Test
@DisplayName("array assertion")
public void array() {assertArrayEquals(new int[]{1, 2}, new int[] {1, 2});
}
- 组合断言
assertAll()方法接受多个 org.junit.jupiter.api.Executable 函数式接口的实例作为要验证的断言,可以通过 lambda 表达式很容易的提供这些断言。
@Test
@DisplayName("assert all")
public void all() {assertAll("Math",() -> assertEquals(2, 1 + 1),() -> assertTrue(1 > 0));
}
- 异常断言
在JUnit4时期,想要测试方法的异常情况时,需要用@Rule注解的ExpectedException变量还是比较麻烦的。而JUnit5提供了一种新的断言方式Assertions.assertThrows(),配合函数式编程就可以进行使用。
断定业务逻辑一定出现异常
@Test
@DisplayName("异常测试")
public void exceptionTest() {ArithmeticException exception = Assertions.assertThrows(//扔出断言异常ArithmeticException.class, () -> System.out.println(1 % 0));
}
- 超时断言
JUnit5还提供了Assertions.assertTimeout()为测试方法设置了超时时间。
@Test
@DisplayName("超时测试")
public void timeoutTest() {//如果测试方法时间超过1s将会异常Assertions.assertTimeout(Duration.ofMillis(1000), () -> Thread.sleep(500));
}
- 快速失败
通过 fail 方法直接使得测试失败。
@Test
@DisplayName("fail")
public void shouldFail() {fail("This should fail");
}
前置条件
assumeTrue 和 assumFalse 确保给定的条件为 true 或 false,不满足条件会使得测试执行终止。
assumingThat 的参数是表示条件的布尔值和对应的 Executable 接口的实现对象。只有条件满足时,Executable 对象才会被执行;当条件不满足时,测试执行并不会终止。
@DisplayName("前置条件")
public class AssumptionsTest {private final String environment = "DEV";@Test@DisplayName("simple")public void simpleAssume() {assumeTrue(Objects.equals(this.environment, "DEV"));assumeFalse(() -> Objects.equals(this.environment, "PROD"));}@Test@DisplayName("assume then do")public void assumeThenDo() {assumingThat(Objects.equals(this.environment, "DEV"),() -> System.out.println("In DEV"));}
}
嵌套测试
@Nested 注解实现嵌套测试,从而可以更好的把相关的测试方法组织在一起。在内部类中可以使用@BeforeEach 和@AfterEach注解,而且嵌套的层次没有限制。
@DisplayName("A stack")
class TestingAStackDemo {Stack<Object> stack;@Test@DisplayName("is instantiated with new Stack()")void isInstantiatedWithNew() {new Stack<>();}@Nested@DisplayName("when new")class WhenNew {@BeforeEachvoid createNewStack() {stack = new Stack<>();}@Test@DisplayName("is empty")void isEmpty() {assertTrue(stack.isEmpty());}@Test@DisplayName("throws EmptyStackException when popped")void throwsExceptionWhenPopped() {assertThrows(EmptyStackException.class, stack::pop);}@Test@DisplayName("throws EmptyStackException when peeked")void throwsExceptionWhenPeeked() {assertThrows(EmptyStackException.class, stack::peek);}@Nested@DisplayName("after pushing an element")class AfterPushing {String anElement = "an element";@BeforeEachvoid pushAnElement() {stack.push(anElement);}@Test@DisplayName("it is no longer empty")void isNotEmpty() {assertFalse(stack.isEmpty());}@Test@DisplayName("returns the element when popped and is empty")void returnElementWhenPopped() {assertEquals(anElement, stack.pop());assertTrue(stack.isEmpty());}@Test@DisplayName("returns the element when peeked but remains not empty")void returnElementWhenPeeked() {assertEquals(anElement, stack.peek());assertFalse(stack.isEmpty());}}}
}
参数化测试
- @ValueSource: 为参数化测试指定入参来源,支持八大基础类以及String类型,Class类型
- @NullSource: 表示为参数化测试提供一个null的入参
- @EnumSource: 表示为参数化测试提供一个枚举入参
- @CsvFileSource:表示读取指定CSV文件内容作为参数化测试入参
- @MethodSource:表示读取指定方法的返回值作为参数化测试入参(注意方法返回需要是一个流)
@ParameterizedTest
@ValueSource(strings = {"one", "two", "three"})
@DisplayName("参数化测试1")
public void parameterizedTest1(String string) {System.out.println(string);Assertions.assertTrue(StringUtils.isNotBlank(string));
}@ParameterizedTest
@MethodSource("method") //指定方法名
@DisplayName("方法来源参数")
public void testWithExplicitLocalMethodSource(String name) {System.out.println(name);Assertions.assertNotNull(name);
}static Stream<String> method() {return Stream.of("apple", "banana");
}
迁移指南
官方文档 - Migrating from JUnit 4
在进行迁移的时候需要注意如下的变化:
- 注解在
org.junit.jupiter.api包中,断言在org.junit.jupiter.api.Assertions类中,前置条件在org.junit.jupiter.api.Assumptions类中。 - 把
@Before和@After替换成@BeforeEach和@AfterEach。 - 把
@BeforeClass和@AfterClass替换成@BeforeAll和@AfterAll。 - 把
@Ignore替换成@Disabled。 - 把
@Category替换成@Tag。 - 把
@RunWith、@Rule和@ClassRule替换成@ExtendWith。
指标监控
未来每一个微服务在云上部署以后,我们都需要对其进行监控、追踪、审计、控制等。SpringBoot就抽取了Actuator场景,使得我们每个微服务快速引用即可获得生产级别的应用监控、审计等功能。
Actuator
- 添加依赖:
<dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-actuator</artifactId>
</dependency>
- 访问
http://localhost:8080/actuator/**。 - 暴露所有监控信息为HTTP。
management:endpoints:enabled-by-default: true #暴露所有端点信息web:exposure:include: '*' #以web方式暴露
- 测试例子
- http://localhost:8080/actuator/beans
- http://localhost:8080/actuator/configprops
- http://localhost:8080/actuator/metrics
- http://localhost:8080/actuator/metrics/jvm.gc.pause
- http://localhost:8080/actuator/metrics/endpointName/detailPath
常使用的端点及开启与禁用
常使用的端点
| ID | 描述 |
|---|---|
auditevents | 暴露当前应用程序的审核事件信息。需要一个AuditEventRepository组件。 |
beans | 显示应用程序中所有Spring Bean的完整列表。 |
caches | 暴露可用的缓存。 |
conditions | 显示自动配置的所有条件信息,包括匹配或不匹配的原因。 |
configprops | 显示所有@ConfigurationProperties。 |
env | 暴露Spring的属性ConfigurableEnvironment |
flyway | 显示已应用的所有Flyway数据库迁移。 需要一个或多个Flyway组件。 |
health | 显示应用程序运行状况信息。 |
httptrace | 显示HTTP跟踪信息(默认情况下,最近100个HTTP请求-响应)。需要一个HttpTraceRepository组件。 |
info | 显示应用程序信息。 |
integrationgraph | 显示Spring integrationgraph 。需要依赖spring-integration-core。 |
loggers | 显示和修改应用程序中日志的配置。 |
liquibase | 显示已应用的所有Liquibase数据库迁移。需要一个或多个Liquibase组件。 |
metrics | 显示当前应用程序的“指标”信息。 |
mappings | 显示所有@RequestMapping路径列表。 |
scheduledtasks | 显示应用程序中的计划任务。 |
sessions | 允许从Spring Session支持的会话存储中检索和删除用户会话。需要使用Spring Session的基于Servlet的Web应用程序。 |
shutdown | 使应用程序正常关闭。默认禁用。 |
startup | 显示由ApplicationStartup收集的启动步骤数据。需要使用SpringApplication进行配置BufferingApplicationStartup。 |
threaddump | 执行线程转储。 |
如果您的应用程序是Web应用程序(Spring MVC,Spring WebFlux或Jersey),则可以使用以下附加端点:
| ID | 描述 |
|---|---|
heapdump | 返回hprof堆转储文件。 |
jolokia | 通过HTTP暴露JMX bean(需要引入Jolokia,不适用于WebFlux)。需要引入依赖jolokia-core。 |
logfile | 返回日志文件的内容(如果已设置logging.file.name或logging.file.path属性)。支持使用HTTPRange标头来检索部分日志文件的内容。 |
prometheus | 以Prometheus服务器可以抓取的格式公开指标。需要依赖micrometer-registry-prometheus。 |
其中最常用的Endpoint:
- Health:监控状况
- Metrics:运行时指标
- Loggers:日志记录
Health Endpoint
健康检查端点,我们一般用于在云平台,平台会定时的检查应用的健康状况,我们就需要Health Endpoint可以为平台返回当前应用的一系列组件健康状况的集合。
重要的几点:
- health endpoint返回的结果,应该是一系列健康检查后的一个汇总报告。
- 很多的健康检查默认已经自动配置好了,比如:数据库、redis等。
- 可以很容易的添加自定义的健康检查机制。
Metrics Endpoint
提供详细的、层级的、空间指标信息,这些信息可以被pull(主动推送)或者push(被动获取)方式得到:
- 通过Metrics对接多种监控系统。
- 简化核心Metrics开发。
- 添加自定义Metrics或者扩展已有Metrics。
开启与禁用Endpoints
- 默认所有的Endpoint除过shutdown都是开启的。
- 需要开启或者禁用某个Endpoint。配置模式为
management.endpoint.<endpointName>.enabled = true
management:endpoint:beans:enabled: true
- 或者禁用所有的Endpoint然后手动开启指定的Endpoint。
management:endpoints:enabled-by-default: false# 关闭总开关,开启分体开关endpoint:beans:enabled: truehealth:enabled: true
暴露Endpoints
支持的暴露方式
- HTTP:默认只暴露health和info。
- JMX:默认暴露所有Endpoint。
- 除过health和info,剩下的Endpoint都应该进行保护访问。如果引入Spring Security,则会默认配置安全访问规则。
| ID | JMX | Web |
|---|---|---|
auditevents | Yes | No |
beans | Yes | No |
caches | Yes | No |
conditions | Yes | No |
configprops | Yes | No |
env | Yes | No |
flyway | Yes | No |
health | Yes | Yes |
heapdump | N/A | No |
httptrace | Yes | No |
info | Yes | Yes |
integrationgraph | Yes | No |
jolokia | N/A | No |
logfile | N/A | No |
loggers | Yes | No |
liquibase | Yes | No |
metrics | Yes | No |
mappings | Yes | No |
prometheus | N/A | No |
scheduledtasks | Yes | No |
sessions | Yes | No |
shutdown | Yes | No |
startup | Yes | No |
threaddump | Yes | No |
若要更改公开的Endpoint,请配置以下的包含和排除属性:
| Property | Default |
|---|---|
management.endpoints.jmx.exposure.exclude | |
management.endpoints.jmx.exposure.include | * |
management.endpoints.web.exposure.exclude | |
management.endpoints.web.exposure.include | info, health |
官方文档 - Exposing Endpoints
定制Endpoint
定制 Health 信息
# management是所有actuator的配置
# management.endpoint.端点名.** 对某个端点的具体配置
management:endpoints:enabled-by-default: trueweb:exposure:include: '*'endpoint:health:show-details: always #总是显示详细信息。可显示每个模块的状态信息
通过实现HealthIndicator 接口,或继承MyComHealthIndicator 类。
import org.springframework.boot.actuate.health.Health;
import org.springframework.boot.actuate.health.HealthIndicator;
import org.springframework.stereotype.Component;@Component
public class MyHealthIndicator implements HealthIndicator {@Overridepublic Health health() {int errorCode = check(); // perform some specific health checkif (errorCode != 0) {return Health.down().withDetail("Error Code", errorCode).build();}return Health.up().build();}}/*
构建Health
Health build = Health.down().withDetail("msg", "error service").withDetail("code", "500").withException(new RuntimeException()).build();
*/
@Component
public class MyComHealthIndicator extends AbstractHealthIndicator {/*** 真实的检查方法* @param builder* @throws Exception*/@Overrideprotected void doHealthCheck(Health.Builder builder) throws Exception {//mongodb。 获取连接进行测试Map<String,Object> map = new HashMap<>();// 检查完成if(1 == 2){
// builder.up(); //健康builder.status(Status.UP);map.put("count",1);map.put("ms",100);}else {
// builder.down();builder.status(Status.OUT_OF_SERVICE);map.put("err","连接超时");map.put("ms",3000);}builder.withDetail("code",100).withDetails(map);}
}
定制info信息
常用两种方式:
- 编写配置文件
info:appName: boot-adminversion: 2.0.1mavenProjectName: @project.artifactId@ #使用@@可以获取maven的pom文件值mavenProjectVersion: @project.version@
- 编写InfoContributor
import java.util.Collections;import org.springframework.boot.actuate.info.Info;
import org.springframework.boot.actuate.info.InfoContributor;
import org.springframework.stereotype.Component;@Component
public class ExampleInfoContributor implements InfoContributor {@Overridepublic void contribute(Info.Builder builder) {builder.withDetail("example",Collections.singletonMap("key", "value"));}}
http://localhost:8080/actuator/info 会输出以上方式返回的所有info信息
定制Metrics信息
Spring Boot支持的metrics
增加定制Metrics:
class MyService{Counter counter;public MyService(MeterRegistry meterRegistry){counter = meterRegistry.counter("myservice.method.running.counter");}public void hello() {counter.increment();}
}
//也可以使用下面的方式
@Bean
MeterBinder queueSize(Queue queue) {return (registry) -> Gauge.builder("queueSize", queue::size).register(registry);
}
定制Endpoint
@Component
@Endpoint(id = "container")
public class DockerEndpoint {@ReadOperationpublic Map getDockerInfo(){//端点的读操作,默认访问地址 /actuator/container ,下面是输出的内容return Collections.singletonMap("info","docker started...");}@WriteOperationprivate void restartDocker(){System.out.println("docker restarted....");}}
场景:
- 开发ReadinessEndpoint来管理程序是否就绪。
- 开发LivenessEndpoint来管理程序是否存活。
自定义starter
starter启动原理
starter只是说要引入哪些依赖
- starter的pom.xml引入autoconfigure依赖
-
autoconfigure包中配置使用
META-INF/spring.factories中EnableAutoConfiguration的值,使得项目启动加载指定的自动配置类 -
编写自动配置类
xxxAutoConfiguration->xxxxProperties -
@Configuration@Conditional@EnableConfigurationProperties@Bean- …
-
引入starter —
xxxAutoConfiguration— 容器中放入组件 ----绑定xxxProperties---- 配置项
自定义starter
-
目标:创建
HelloService的自定义starter。 -
创建两个工程,分别命名为
hello-spring-boot-starter(普通Maven工程),hello-spring-boot-starter-autoconfigure(需用用到Spring Initializr创建的Maven工程)。 -
hello-spring-boot-starter无需编写什么代码,只需让该工程引入hello-spring-boot-starter-autoconfigure依赖:
<?xml version="1.0" encoding="UTF-8"?>
<project xmlns="http://maven.apache.org/POM/4.0.0"xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation="http://maven.apache.org/POM/4.0.0 http://maven.apache.org/xsd/maven-4.0.0.xsd"><modelVersion>4.0.0</modelVersion><groupId>com.lun</groupId><artifactId>hello-spring-boot-starter</artifactId><version>1.0.0-SNAPSHOT</version><dependencies><dependency><groupId>com.lun</groupId><artifactId>hello-spring-boot-starter-autoconfigure</artifactId><version>1.0.0-SNAPSHOT</version></dependency></dependencies></project>
hello-spring-boot-starter-autoconfigure的pom.xml如下:
<?xml version="1.0" encoding="UTF-8"?>
<project xmlns="http://maven.apache.org/POM/4.0.0" xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation="http://maven.apache.org/POM/4.0.0 https://maven.apache.org/xsd/maven-4.0.0.xsd"><modelVersion>4.0.0</modelVersion><parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version>2.4.2</version><relativePath/> <!-- lookup parent from repository --></parent><groupId>com.lun</groupId><artifactId>hello-spring-boot-starter-autoconfigure</artifactId><version>1.0.0-SNAPSHOT</version><name>hello-spring-boot-starter-autoconfigure</name><description>Demo project for Spring Boot</description><properties><java.version>1.8</java.version></properties><dependencies><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter</artifactId></dependency></dependencies>
</project>
- 创建4个文件:
com/lun/hello/auto/HelloServiceAutoConfigurationcom/lun/hello/bean/HelloPropertiescom/lun/hello/service/HelloServicesrc/main/resources/META-INF/spring.factories
import com.lun.hello.bean.HelloProperties;
import com.lun.hello.service.HelloService;
import org.springframework.boot.autoconfigure.condition.ConditionalOnMissingBean;
import org.springframework.boot.context.properties.EnableConfigurationProperties;
import org.springframework.context.annotation.Bean;
import org.springframework.context.annotation.Configuration;@Configuration
@ConditionalOnMissingBean(HelloService.class)
@EnableConfigurationProperties(HelloProperties.class)//默认HelloProperties放在容器中
public class HelloServiceAutoConfiguration {@Beanpublic HelloService helloService(){return new HelloService();}}
import org.springframework.boot.context.properties.ConfigurationProperties;@ConfigurationProperties("hello")
public class HelloProperties {private String prefix;private String suffix;public String getPrefix() {return prefix;}public void setPrefix(String prefix) {this.prefix = prefix;}public String getSuffix() {return suffix;}public void setSuffix(String suffix) {this.suffix = suffix;}
}import com.lun.hello.bean.HelloProperties;
import org.springframework.beans.factory.annotation.Autowired;/*** 默认不要放在容器中*/
public class HelloService {@Autowiredprivate HelloProperties helloProperties;public String sayHello(String userName){return helloProperties.getPrefix() + ": " + userName + " > " + helloProperties.getSuffix();}
}
# Auto Configure
org.springframework.boot.autoconfigure.EnableAutoConfiguration=\
com.lun.hello.auto.HelloServiceAutoConfiguration
-
用maven插件,将两工程install到本地。
-
接下来,测试使用自定义starter,用Spring Initializr创建名为
hello-spring-boot-starter-test工程,引入hello-spring-boot-starter依赖,其pom.xml如下:
<?xml version="1.0" encoding="UTF-8"?>
<project xmlns="http://maven.apache.org/POM/4.0.0" xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation="http://maven.apache.org/POM/4.0.0 https://maven.apache.org/xsd/maven-4.0.0.xsd"><modelVersion>4.0.0</modelVersion><parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version>2.4.2</version><relativePath/> <!-- lookup parent from repository --></parent><groupId>com.lun</groupId><artifactId>hello-spring-boot-starter-test</artifactId><version>1.0.0-SNAPSHOT</version><name>hello-spring-boot-starter-test</name><description>Demo project for Spring Boot</description><properties><java.version>1.8</java.version></properties><dependencies><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter</artifactId></dependency><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-test</artifactId><scope>test</scope></dependency><!-- 引入`hello-spring-boot-starter`依赖 --><dependency><groupId>com.lun</groupId><artifactId>hello-spring-boot-starter</artifactId><version>1.0.0-SNAPSHOT</version></dependency></dependencies><build><plugins><plugin><groupId>org.springframework.boot</groupId><artifactId>spring-boot-maven-plugin</artifactId></plugin></plugins></build></project>- 添加配置文件
application.properties:
hello.prefix=hello
hello.suffix=666
- 添加单元测试类:
import com.lun.hello.service.HelloService;//来自自定义starter
import org.junit.jupiter.api.Assertions;
import org.junit.jupiter.api.Test;
import org.springframework.beans.factory.annotation.Autowired;
import org.springframework.boot.test.context.SpringBootTest;@SpringBootTest
class HelloSpringBootStarterTestApplicationTests {@Autowiredprivate HelloService helloService;@Testvoid contextLoads() {// System.out.println(helloService.sayHello("lun"));Assertions.assertEquals("hello: lun > 666", helloService.sayHello("lun"));}}
SpringBoot完整启动过程
-
加载配置文件
Spring Boot 应用程序启动时,会自动加载 application.properties 或 application.yml 配置文件中的属性。这些属性可以通过 @Value 注解或 @ConfigurationProperties 注解注入到代码中。 -
创建 Spring 容器
Spring Boot 会自动创建 Spring 容器,并加载所有的组件,包括控制器、服务、仓库等。Spring 容器会根据依赖注入(DI)和面向切面编程(AOP)等原理,完成组件之间的依赖关系和处理逻辑。 -
扫描组件
Spring Boot 会扫描项目中的所有组件,包括控制器、服务、仓库等,并将其加载到 Spring 容器中。 -
启动 Tomcat
Spring Boot 应用程序中默认集成了 Tomcat 服务器。启动 Spring Boot 应用程序时,会自动启动内嵌的 Tomcat 服务器,提供 HTTP 服务。 -
处理请求
Tomcat 接收到请求后,会将其转发给 Spring Boot 应用程序。Spring Boot 应用程序会根据请求的 URL,匹配到对应的控制器,并调用相应的方法处理请求。 -
返回响应
处理完请求后,Spring Boot 应用程序会将处理结果封装成相应的 HTTP 响应,返回给客户端。
总的来说,Spring Boot 应用程序的启动过程是一个自动化的过程,可以快速地搭建出一个 Web 应用程序,并提供相应的 HTTP 服务。
