域名做非法网站手机如何登入网站服务器
前言
如果在Ubuntu上使用qt开发可移植到周立功开发板的应用程序,需要在Ubuntu上交叉编译用于移植的Qt库,具体做法如下:
1、下载源码
源码qt-everywhere-opensource-src-5.9.6.tar.xz拷贝到ubuntu自建的software文件下
2、解压
点击提取到此处
3、安装配置
运行脚本文件进行安装配置。
3.1 创建脚本
进入qt-everywhere-opensource-src-5.9.6目录,创建脚本,脚本名称自己定义build.h,编写内容。可以参考周立功原系统中提供的脚本文件(虚拟机打开的镜像work文件下)
内容如下:
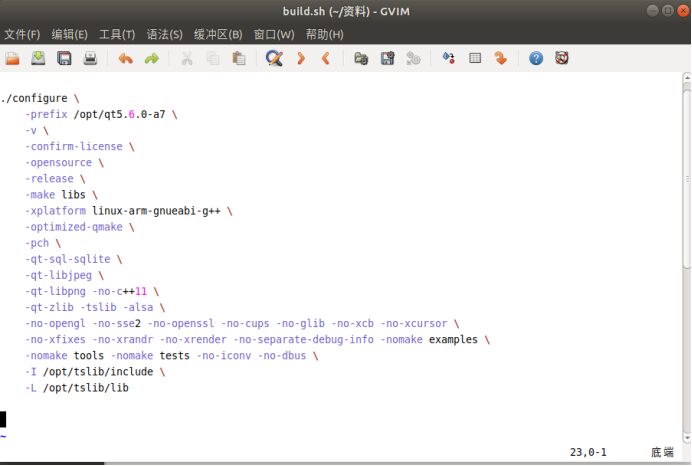
将该文件复制到qt-everywhere-opensource-src-5.9.6目录下。
双击打开,按i键进入到插入模式,然后对其修改保存,修改后内容如下:
此处仅对安装路径进行修改。-I和-L(链接库)作用是引用触摸屏的头文件和库文件。
