中国摄影师个人网站设计临清网站开发
起因:Node进程吃满CPU


分析
我发现每次使用vscode的remote插件登陆到server后,就会出现node进程,不太清楚干什么用的,但是绝对和它有关。
查找原因
首先找到了这篇文章,解决了rg进程的问题:
https://blog.csdn.net/sigmarising/article/details/107615035
其评论区有个朋友给出了解决方案:修补libc6共享库
这里他发的wget链接挂了,不过,这也给我们提供了libc6关键字
继续搜索:“vscode node libc6 cpu占满”
可以看到有github的讨论:
https://github.com/microsoft/vscode-remote-release/issues/2921
进入,看到了解决方法:
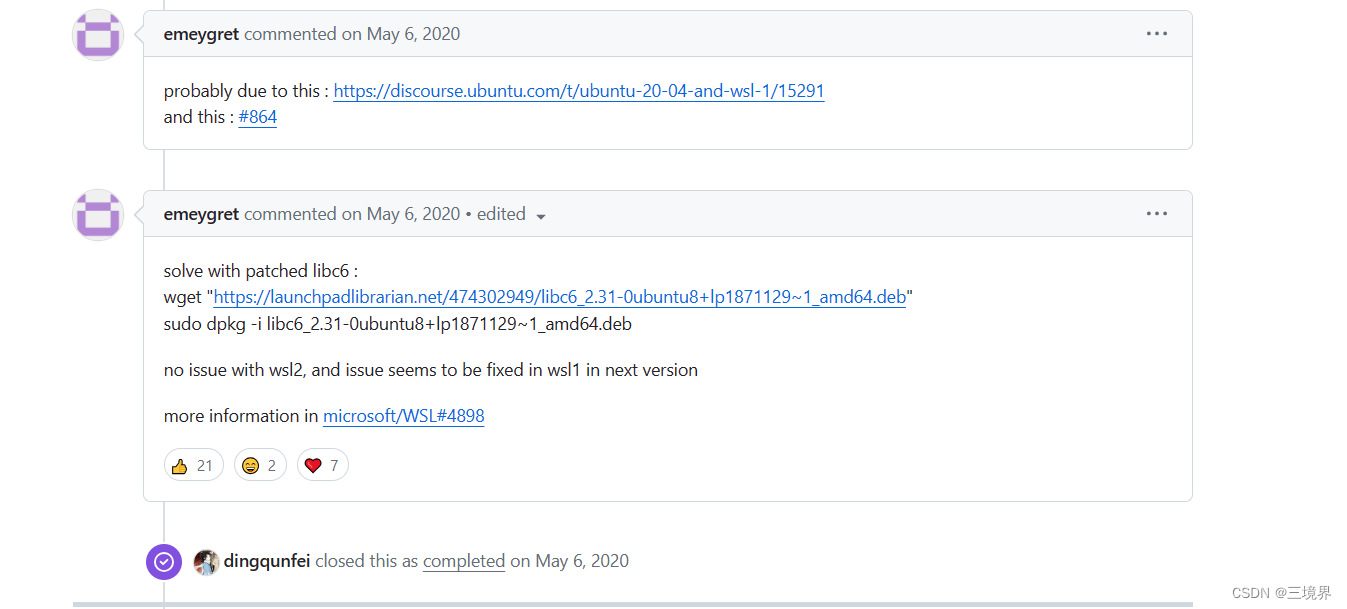
简而言之就是下载一个libc6,然后dpkg安装!但是这里的链接还是不能用,无奈,返回浏览器首页,搜索libc6 amd64 ubuntu:
https://pkgs.org/search/?q=libc6
进到这个链接,找到ubuntu9的deb,下载,dpkg安装。
中间有个小插曲,出现了一个warning:提示/lib/libdwarf.so.0 is not a symbolic link
解决:备份/lib/libdwarf.so.0,然后删除/lib/libdwarf.so.0,再执行dpkg安装即可。
安装后top一下,node还是存在,且占满CPU100%。受不了了,打算开始用source insight
转而一想,最初那个CSDN的链接,评论区有个大佬说过可以把vscode-server删了试试:

我直接用windows终端 ssh到 服务器,把~/.vscode-server/下的内容删光。再开启vsc看看,还是吃满。有可能是有node进程依然存活,删除时被占用,无法杀死。再试试他说的kill,果然成功!
node不再吃满CPU!

