做夹具需要知道的几个网站网站开发的意义和目的
操作系统核心知识点整理--内存篇
- 按段对内存进行管理
- 内存分区
- 内存分页
- 为什么需要多级页表
- TLB解决了多级页表什么样的缺陷?
- TLB缓存命中率高的原理是什么?
- 段页结合: 为什么需要虚拟内存?
- 虚拟地址到物理地址的转换过程
- 段页式管理下程序如何载入内存?
- 页面置换
- 总结
- 推荐阅读
本文主要面向应用层软件开发人员整理一篇必须了解的操作系统核心知识图谱,每小节参考文章链接都已经在小节末尾给出,如果大家有疑问,可以评论区留言,或者直接去阅读原文。
按段对内存进行管理
为什么程序要按段载入内存?
- 如果我们直接将程序代码全部放到内存中,这不利于内存的利用和程序的运行,因为,通常程序被编译后都会分为多个段,各个段都有其各自的特点,如: 代码段只读,栈段和堆可以动态扩展。
- 因此,通常会将程序分段载入内存中来,如果不进行分段载入,如果程序栈空间不足,需要扩展,就需要复制整个程序代码到新分配好的更大的内存空间才可以。
内存分段管理是怎么个玩法 ?
- 每个进程需要关联一个段表,用于记录当前进程对应程序的各个段信息,如: 段的基址,段的限长,段的特权级等
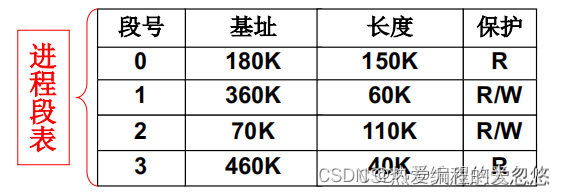
- 程序分段载入内存,这个过程中需要不断为每个段在内存中寻找空闲分区
- 同时在对应进程的段表中添加一条表项,记录当前段的存放位置等信息
内存分区
如果我们采用内存分区的方式来对物理内存进行管理,那么此时我们有两种选择:
- 固定分区
- 可变分区
显然,我们程序的各个段的大小都是不固定的,因此固定分区可以排除。
如果采用可变分区进行管理,我们需要使用空闲分区表或者空闲分区链表的方式来记录当前内存中各个空闲分区块。
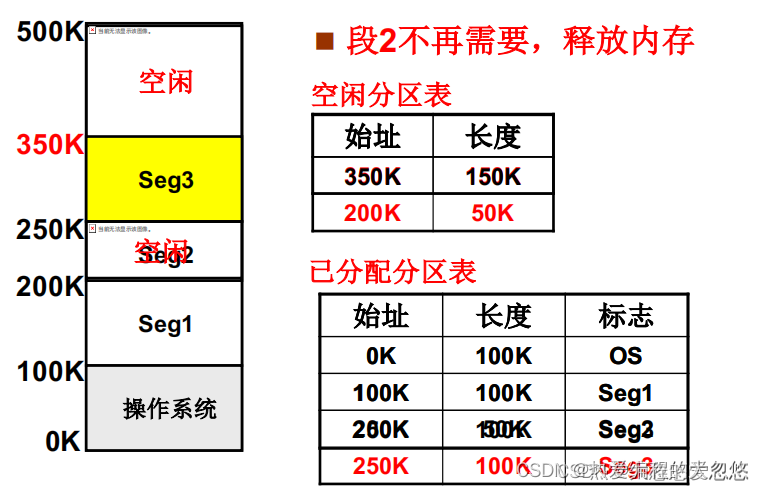
当接受到一个段内存申请请求时,我们可以采用: 首次适配,最佳适配,最差适配,首次循环适配等算法来进行内存的分配。
但是无论采用何种分配算法,都容易导致内存碎片的产生,随着分配次数的增加,内存碎片越来越多,当某个内存申请请求发起后,发现只有内部内存碎片才能完成内存分配时,这时候就需要进行内存紧缩。
内存紧缩需要花费的时间开销很大,这个过程中cpu无法访问内存,给用户的感觉就是操作系统死机了。
内存分页
想要解决内存分区导致的内存碎片问题,最简单的方法就是采用内存分页,针对每个段的内存请求,系统一页一页的分配给这个短,加入这个段需要3页半的大小的内存,那我就分配给他四整页的内存。

当我们将段数据打散存放到多个页中时,由于四个物理页的顺序未必是连续的,所以我们需要将分配给段0的页进行编号,这里的编号我们称为虚页号,那么下一个问题就来了,如何根据虚页号定位物理页号呢?
- 页表: 存放虚页号到物理页号的映射关系
如果对物理内存采用分页管理,那么此时我们程序发出的逻辑地址就由虚页号+页内偏移组成了,通过查询页表将虚页号转换为对应的物理页号,最终计算出物理地址:
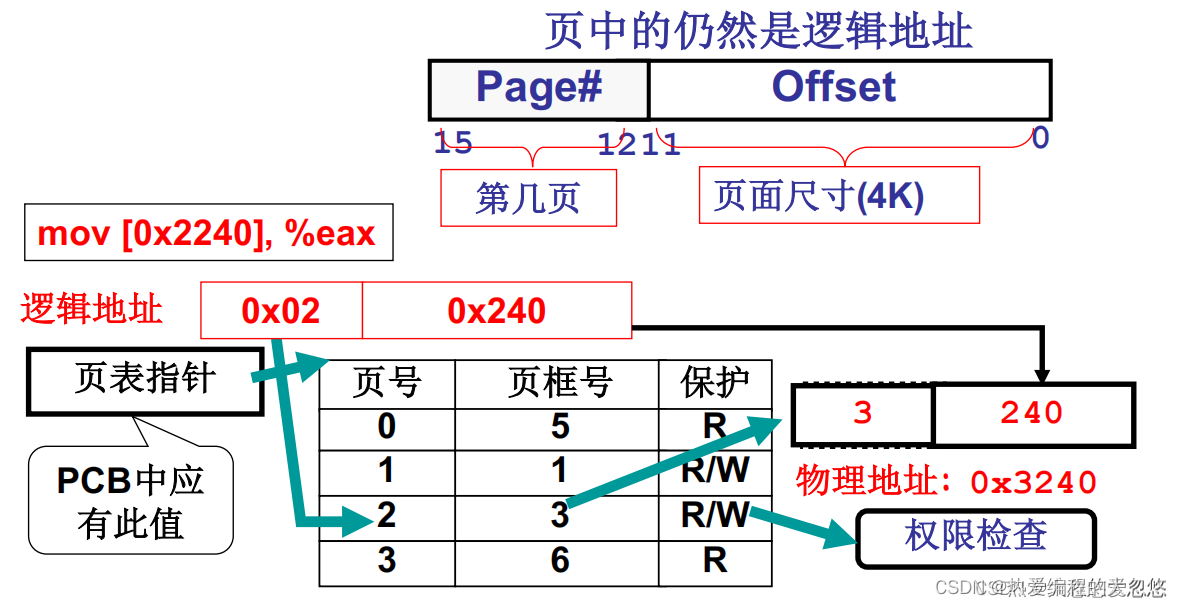
为了实现页表的快速查询,在页表中虚页号不直接提供,而是作为页表数组的索引隐含其中,但是这就意味着页表必须要连续的内存存储。
为什么需要多级页表
以Linux 0.11中每页4K进行计算,对于32位操作系统而言,其发出的32位的虚拟地址最多可以定位到1M的页数。
那么就意味着页表需要维护1M个虚拟页号和物理页号的映射关系,那么页表占据的内存就会很大。
解决这个问题有两种思路:
- 由于大部分逻辑地址用不到,因此我们只在页表中存储用到的虚页号,如果采取这个办法,那么我们就无法通过虚页号快速定位到页表中的具体表项了,可能需要多出几千次额外内存访问。–> 页表必须是顺序排列的,没用到的虚页号也必须保留,这样才能够以一次访存的代价定位到具体的表项。
- 多级页表:
我们目前遇到的困境是: 页表项太多,并且要求页表中的页表项是连续存放的,不管当前虚页号是否用到。
解决思路: 借鉴书目录与小节的思想,将页表项分散存储到多个页表中,各个页表内的页表项是连续存储的,然后通过页目录管理多个页表,确保多个页表之间的顺序性,从而就保证了页表项整体顺序性。

引入了多级页表中,我们的页目录中的页目录项都是连续存放的,每个页目录项指向一个页表,这保证了多个页表之间的顺序性。
当前进程只需要载入自己需要的页目录项指向的页表到内存即可,至于自己用不到的页目录项,则无需载入其对应的页表到内存,这样可以大大节约内存,并且访问次数也只需要两次即可。
同时只有一级页表才总是需要缓存在内存中的,对于二级页表而言,也只会在需要用到的时候才申请内存进行创建,这对于一个普通程序而言,在虚拟地址空间大部分都是未分配的情况下,会节约大量的内存。
TLB解决了多级页表什么样的缺陷?
多级页表的缺陷: 相比于单级页表,层级每增加一级,都需要多出一个访问内存的开销。
但是为了保证页表项的整体连续性,并且还要减少页表对内存的浪费,就必须采用多级页表的形式,但是多级页表时间上的不足,就需要通过缓存来弥补了,也就是TLB。
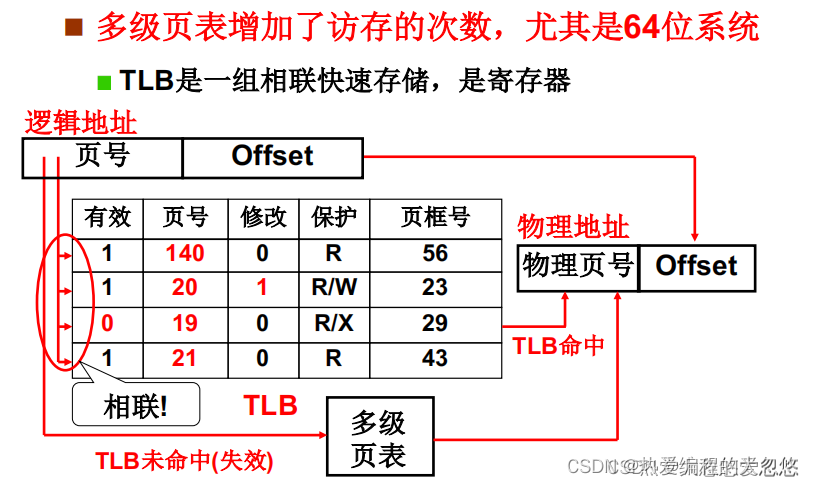
通过CPU内部的TLB寄存器,来缓存最近使用到的页,并且因为TLB采用的是相联存储设计,硬件可以直接通过虚页号定位到缓存中某个表项,然后直接得到对应的物理页号,从而计算出物理地址。
TLB缓存命中率高的原理是什么?
程序访问存在局部性原理,通常在某个时间段内,只会频繁某几个页面号,那么因为TLB缓存了对应的页面号,所以命中率就很高。
段页结合: 为什么需要虚拟内存?
首先,我们的程序需要按段载入内存,如果按照上面最终敲定的内存分页方案,那么我们程序的各个段都会被打散存放到多个不相邻或者相邻的物理页上,当然还需要给每个物理页编排一个虚拟页号,用于还原段,这个过程中使用页表完成虚页号到物理页号的映射关系:
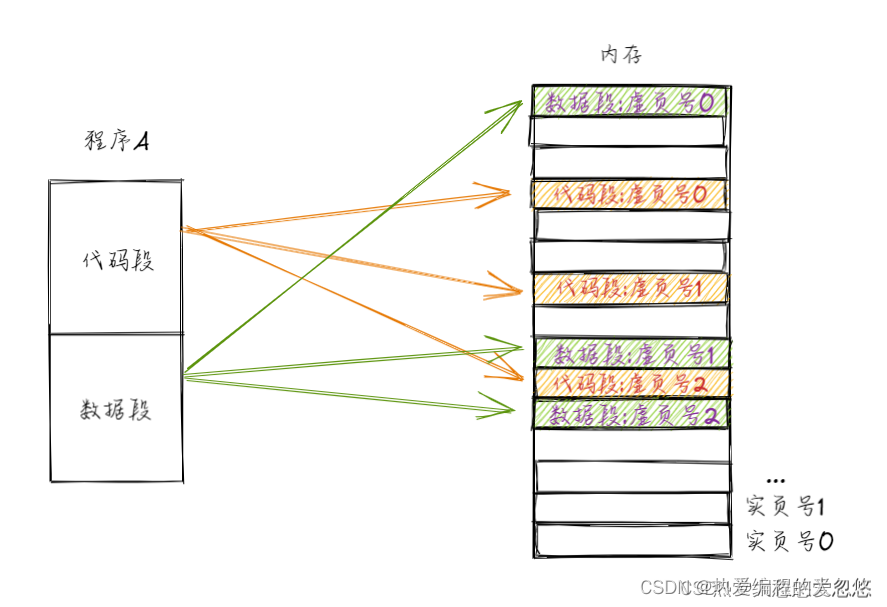
这种方式对于内存的管理而言非常友好,不会造成内存碎片,但是站在程序的视角来看,段内的内存是不连续的。
我们开发者更希望看到的进程内存图是各个段在内存上连续存放:
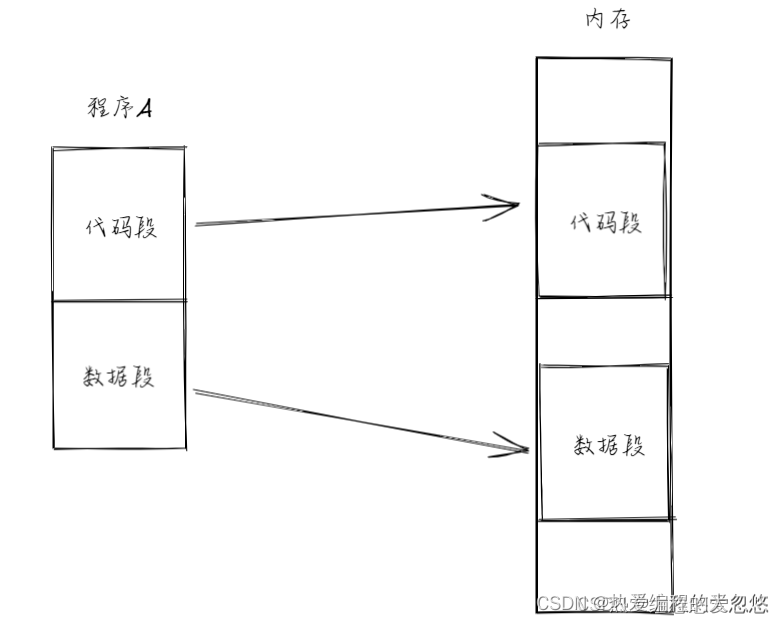
问题: 能否站在程序员的视角看来,程序分段存放在内存上的模样是连续的,但是站在物理内存视角看来,却是分页管理的呢?
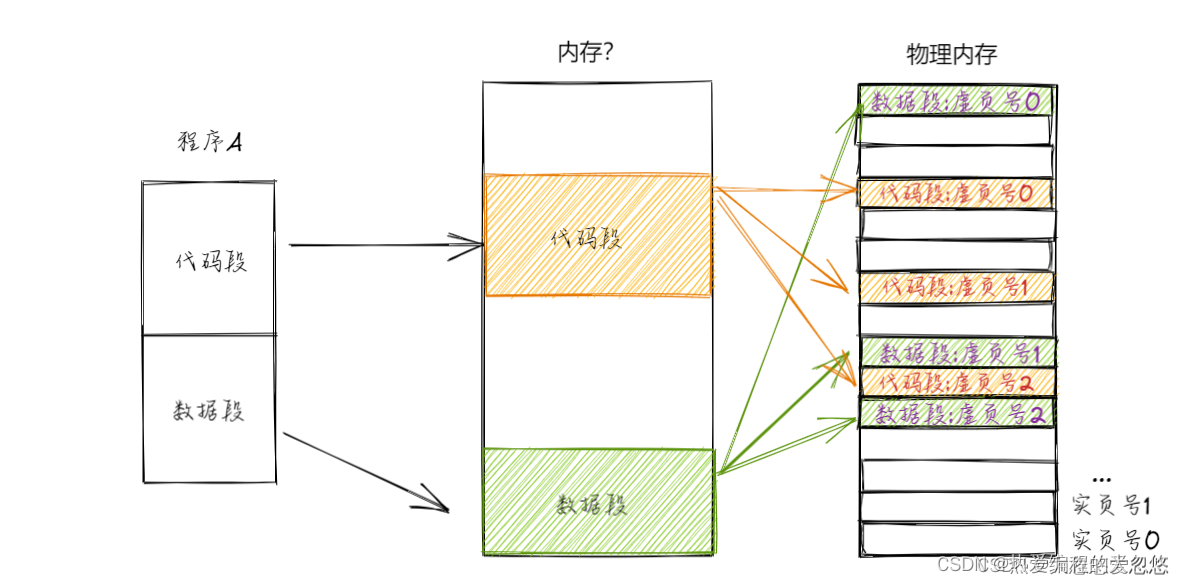
为了实现呈现给上层用户段连续存放的内存图模型,操作系统提供了对应虚拟内存来解决这个问题。
有了虚拟内存的之后,用户写的程序首先在虚拟内存中划分出对应的空间来存放,但是实际程序载入内存时,却会根据先前划分的虚拟地址空间,分别打散存储到对应多个物理页上。
当用户想要访问内存时,也只需要面向虚拟内存操作即可,用户发出的地址都是虚拟地址,但是操作系统通过将虚拟地址映射到物理地址后,用户就可以正常读取和设置物理内存中的数据了,对于用户而言操作虚拟内存和物理内存无区别。
段页结合的关键在于:用户能够看到的虚拟内存中,段是连续存放在内存中,而实际的物理内存依然采用分页管理,所以对应各个程序段依然会被打散存储到各个物理页中,这个过程对用户无感。
虚拟地址到物理地址的转换过程
引入段页结合内存管理后,用户程序发出的虚拟地址重定向到物理地址的过程也发生了很大变化:
- 首先,用户发出的虚拟地址由段号+段内偏移组成,通过查询段表,获得段基址,拼接段内偏移,得到虚拟地址
- 虚拟地址,经过MMU计算,得到虚拟页号,然后查询对应的页表,得到真实的物理页号
- 通过真实的物理页号+页内偏移,得到最终物理地址
具体通过MMU完成虚拟地址到物理地址转换过程,可以参考本文
段页式管理下程序如何载入内存?
- 首先在虚拟内存中通过分区适配算法,找到一块空闲分区来存放程序中的段,这里实际是在对应的段表中新增一条表项,记录当前段在虚拟内存中的段基址和段限长等信息。
- 将虚拟内存中分配的段空间打散,按照对应的分页机制,映射到若干物理页上,由对应的页表保存虚页号到物理页号的映射关系。
- 配合磁盘读写,将程序分段读入到对应的物理页上。
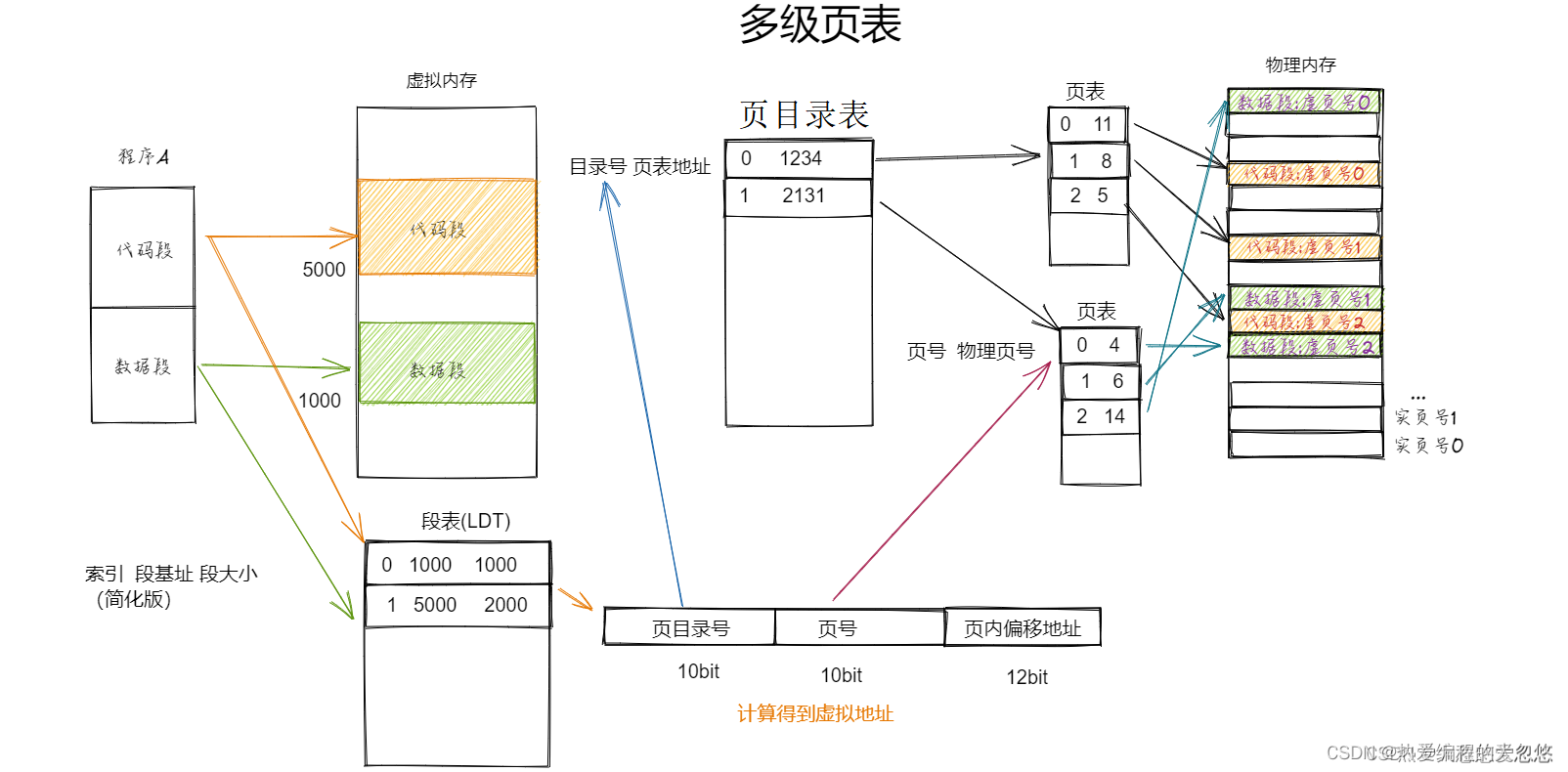
当用户需要访存时,首先通过段号,查询段表,得到段基址; 然后拼接段内偏移地址得到虚拟地址,再通过对应的分页机制,解析出虚拟地址对应到页表中哪一个表项,然后得到对应的物理页号,通过物理页号就可以轻松计算出物理页号的基址,加上页内偏移地址,最终计算出实际的物理地址。
页面置换
地址映射过程中,如果访问页表访问对应的页面不在内存,或者还未建立映射关系,则会发生缺页中断。
当发生缺页中断时,如果当前内存中没有空闲页面,操作系统就必须在内存中选择一个页面移出内存,以便为即将调入的页面让出空间。
具体选择淘汰哪一个页的规则叫做页面置换算法,常见的有:
- 先进先出(FIFO)
- 最近最久未使用(LRU)
- Clock算法,LRU的近似实现
操作系统内存换出—15
包括还需要限制每个进程所能分配到的页面数,即当前进程的工作集,每次要置换页面时,只会在当前进程的工作集中选择并进行淘汰。
总结
- 谈谈内存分段管理和分页管理的联系
我们编写的程序编译后都是分段的,因此程序载入内存的过程也应该是分段载入,但是分段对内存进行管理,会产生大量内存碎片,并且内存紧缩的过程也非常耗时。
所以采用分页管理后,内存空间利用率会提供,不会产生外部碎片,只会有少量页内碎片。
但是分页管理的缺点在于不方便按照模块实现信息的共享和保护,而采用分段的方式则非常容易实现。
所以,最终的一个解决方案是程序按段载入内存,然后被打散存储到各个物理页上,通过页表完成虚拟页号到物理页号的映射关系。
- 聊聊多级页表的作用吧
在Linux 0.11环境下,每个物理页大小为4k,那么在32位系统环境下,其发出的32位虚拟地址最多可以定位到1M的页数。那么就意味着我们的页表需要连续存放1M个页表项,页表会占据很多内存。
引入多级页表可以解决页表占据内存过大的问题,通过引入页目录层,我们的进程只需要加载那些使用到的页目录项指向的页表到内存即可,其他页目录项指向的页表则无需载入内存,从而可以大大减少页表占据的内存。
并且也只需要将页目录缓存在内存中,其中的页目录项指向的页表,也可以得到第一次使用到时,才申请内存进行创建。
- tlb有什么作用呢
多级页表可以减少页表占据内存过大的问题,但是也导致一次访存请求,会额外多出n次多级页表查询请求,为了解决这个问题,就引入了缓存来弥补多级页表在时间上不足。
tlb作为CPU内部的相联存储寄存器,用来缓存最近访问过的虚拟页号和物理页号的映射关系,利用的是程序执行的局部性原理,可以有很高的命中率。
- 什么是虚拟内存,为什么需要虚拟内存,虚拟内存有什么好处?
什么是虚拟内存: 虚拟内存为每个进程提供了一个一致性,连续的,私有的地址空间,它让每个进程产生了一种自己在独享主存的错觉。
为什么需要虚拟内存: 为了给用户呈现出一个按段加载,并且各个段在内存中连续存放的内存视图,方便用户编写程序。
虚拟内存好处:
- 给用户呈现一个连续的一致性内存视图,使程序编写难度降低。
- 把内存范围扩展到了硬盘: 加载程序时,可以只加载需要使用到的段,并且程序运行过程中,也可以将不常访问的段换出到磁盘存储。有的操作系统还可以在内存不足的情况下,将某一进程内存全部放入硬盘空间中,并在切换到进程时再从硬盘读取。
- 对于共享库的实现非常方便,只需要将不同进程对应的虚拟地址空间中划分出一块地址空间映射到同一个物理内存区域即可。
推荐阅读
CSAPP,操作系统导论,哈工大操作系统课程
虚拟内存的那点事儿
