当前位置： 首页 > news >正文

优秀服装网站设计网站建设的可研设计报告

news 2025/11/7 17:56:05
优秀服装网站设计,网站建设的可研设计报告,企业展示型网站源码,成都房地产管理局目录 💥1 概述 📚2 运行结果 🎉3 参考文献 👨‍💻4 Matlab代码 💥1 概述 本代码说明了“最小二乘支持向量机”在学习偏微分方程 （PDE） 解方面的应用。提供了一个示例&#xff0c…

       目录

💥1 概述

📚2 运行结果

🎉3 参考文献

👨‍💻4 Matlab代码

💥1 概述

本代码说明了“最小二乘支持向量机”在学习偏微分方程 （PDE） 解方面的应用。提供了一个示例，并将获得的结果与精确的解决方案进行比较。

📚2 运行结果

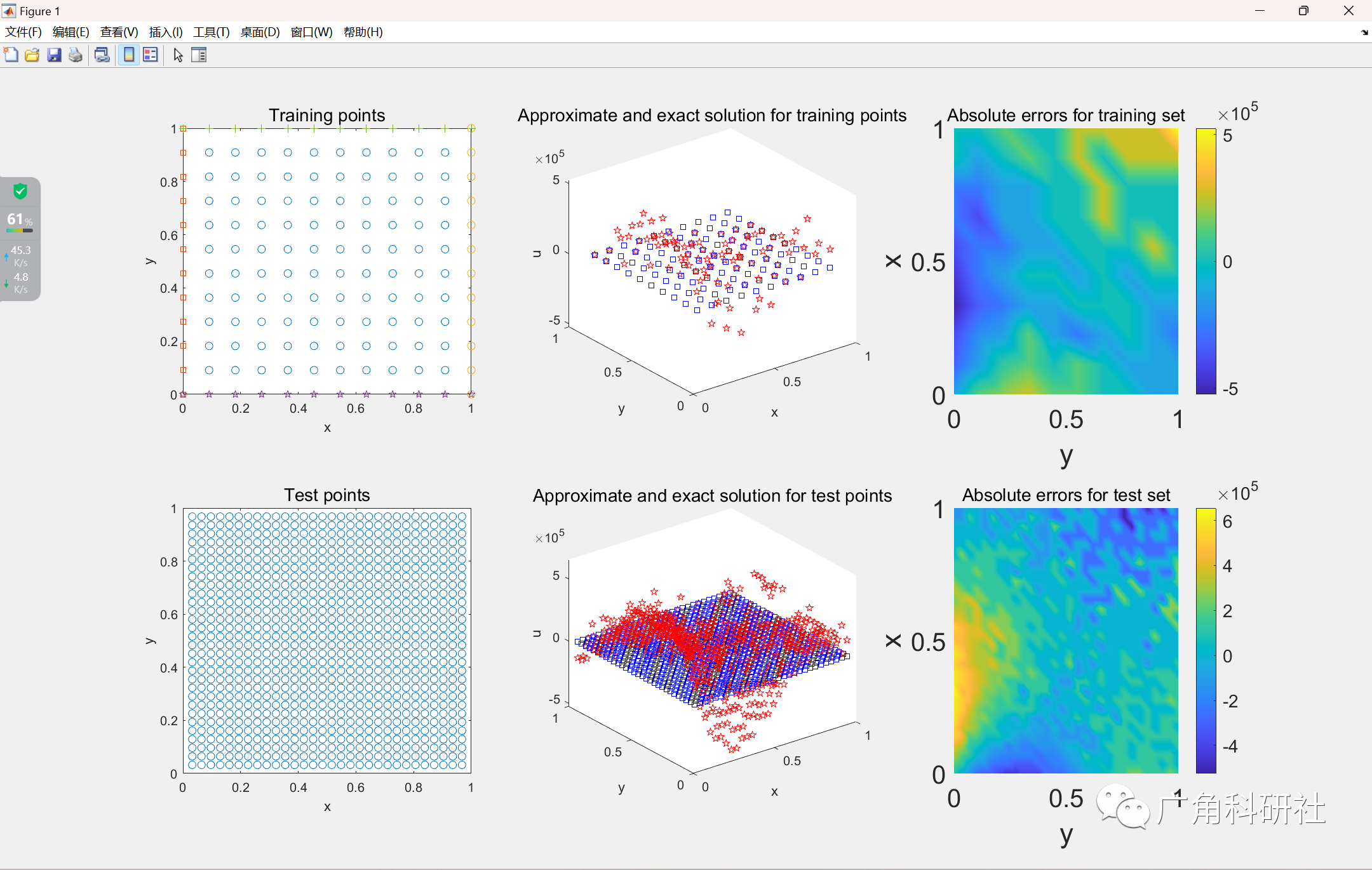
主函数部分代码：

clc; clear all; close all

warning('off','all')

a0=0;

b0=1;

n=11;

h=(b0-a0)/n;

[X1,Y1]=meshgrid(a0+h:h:b0-h);

W=[];

for i=1:size(X1,2)

    Z=[X1(:,i),Y1(:,1)];

    W=[W ; Z];

end

subplot(2,3,1)

plot(W(:,1),W(:,2),'o')

hold on

[X,Y]=meshgrid(a0:h:b0);

W2=[];

for i=1:size(X,2)

    Z=[X(:,i),Y(:,1)];

    W2=[W2 ; Z];

end

L1=[];

for i=1:n+1

    L1=[L1 ; W2(i,:)];

end

L2=[];

for i=n*(n+1)+1:size(W2,1)

    L2=[L2 ; W2(i,:)];

end

L3=[L1(:,2) L1(:,1)];

L4=[L2(:,2) L2(:,1)];

plot(L1(:,1),L1(:,2),'s')

plot(L2(:,1),L2(:,2),'o')

plot(L3(:,1),L3(:,2),'p')

plot(L4(:,1),L4(:,2),'+')

title('Training points','Fontsize',14)

xlabel('x')

ylabel('y')

%% 

f=@(s,v) exp(-s).*(s-2+v.^3+6*v); % right hand side of the given PDE

gamma=10^14; % the regularization parameter

sig=0.95;  % kernel bandwidth

K=KernelMatrix(W,'RBF_kernel',sig);

x=W(:,1);

y=W(:,2);

xx1=x*ones(1,size(x,1));

xx2=x*ones(1,size(x,1));

cof1=2*(xx1-xx2')/(sig);

xx3=y*ones(1,size(y,1));

xx4=y*ones(1,size(y,1));

cof2=2*(xx3-xx4')/(sig);

Kxx=(-2/sig)*K + (cof1.^2) .* K;

Kyy=(-2/sig)*K + (cof2.^2) .* K;

Kx2x2=(   ( 12/(sig^2) - (12/sig)* (cof1.^2) +  (cof1.^4) ) .*K);

Ky2y2=(   ( 12/(sig^2) - (12/sig)* (cof2.^2) +  (cof2.^4) ) .*K);

Kx2y2=(   ( 4/(sig^2) - (2/sig)* (cof1.^2) - (2/sig)* (cof2.^2)  +  (cof1.^2).*(cof2.^2)  ) .*K);

Ky2x2=(   ( 4/(sig^2) - (2/sig)* (cof1.^2) - (2/sig)* (cof2.^2)  +  (cof1.^2).*(cof2.^2)  ) .*K);

K1T= Kx2x2+ Kx2y2 + Ky2x2+ Ky2y2;

m=size(K1T,1);

%*******************************************************************

KL1=KernelMatrix(W,'RBF_kernel',sig,L1);

L1b1x=L1(:,1)*ones(1,size(x,1));

L1b2x=x*ones(1,size(L1(:,1),1));

cofL1x=-2*(L1b1x'-L1b2x)/(sig);

L1b1y=L1(:,2)*ones(1,size(y,1));

L1b2y=y*ones(1,size(L1(:,2),1));

cofL1y=-2*(L1b1y'-L1b2y)/(sig);

KL1xx=(-2/sig)*KL1 + (cofL1x.^2) .* KL1;

KL1yy=(-2/sig)*KL1 + (cofL1y.^2) .* KL1;

KL1T= KL1xx+ KL1yy;

%*************************************************

KL2=KernelMatrix(W,'RBF_kernel',sig,L2);

L2b1x=L2(:,1)*ones(1,size(x,1));

L2b2x=x*ones(1,size(L2(:,1),1));

cofL2x=-2*(L2b1x'-L2b2x)/(sig);

L2b1y=L2(:,2)*ones(1,size(y,1));

L2b2y=y*ones(1,size(L2(:,2),1));

cofL2y=-2*(L2b1y'-L2b2y)/(sig);

KL2xx=(-2/sig)*KL2 + (cofL2x.^2) .* KL2;

KL2yy=(-2/sig)*KL2 + (cofL2y.^2) .* KL2;

KL2T= KL2xx+ KL2yy;

%*************************************************

KL3=KernelMatrix(W,'RBF_kernel',sig,L3);

L3b1x=L3(:,1)*ones(1,size(x,1));

L3b2x=x*ones(1,size(L3(:,1),1));

cofL3x=-2*(L3b1x'-L3b2x)/(sig);

L3b1y=L3(:,2)*ones(1,size(y,1));

L3b2y=y*ones(1,size(L3(:,2),1));

cofL3y=-2*(L3b1y'-L3b2y)/(sig);

KL3xx=(-2/sig)*KL3 + (cofL3x.^2) .* KL3;

KL3yy=(-2/sig)*KL3 + (cofL3y.^2) .* KL3;

KL3T= KL3xx+ KL3yy;

%*************************************************

KL4=KernelMatrix(W,'RBF_kernel',sig,L4);

L4b1x=L4(:,1)*ones(1,size(x,1));

L4b2x=x*ones(1,size(L4(:,1),1));

cofL4x=-2*(L4b1x'-L4b2x)/(sig);

L4b1y=L4(:,2)*ones(1,size(y,1));

L4b2y=y*ones(1,size(L4(:,2),1));

cofL4y=-2*(L4b1y'-L4b2y)/(sig);

KL4xx=(-2/sig)*KL4 + (cofL4x.^2) .* KL4;

KL4yy=(-2/sig)*KL4 + (cofL4y.^2) .* KL4;

KL4T= KL4xx+ KL4yy;

%*************************************************

KL1L1=KernelMatrix(L1,'RBF_kernel',sig,L1);

KL2L1=KernelMatrix(L2,'RBF_kernel',sig,L1);

KL3L1=KernelMatrix(L3,'RBF_kernel',sig,L1);

KL4L1=KernelMatrix(L4,'RBF_kernel',sig,L1);

%*************************************************

KL1L2=KernelMatrix(L1,'RBF_kernel',sig,L2);

KL2L2=KernelMatrix(L2,'RBF_kernel',sig,L2);

KL3L2=KernelMatrix(L3,'RBF_kernel',sig,L2);

KL4L2=KernelMatrix(L4,'RBF_kernel',sig,L2);

%************************************************

KL1L3=KernelMatrix(L1,'RBF_kernel',sig,L3);

KL2L3=KernelMatrix(L2,'RBF_kernel',sig,L3);

KL3L3=KernelMatrix(L3,'RBF_kernel',sig,L3);

KL4L3=KernelMatrix(L4,'RBF_kernel',sig,L3);

%************************************************

KL1L4=KernelMatrix(L1,'RBF_kernel',sig,L4);

KL2L4=KernelMatrix(L2,'RBF_kernel',sig,L4);

KL3L4=KernelMatrix(L3,'RBF_kernel',sig,L4);

KL4L4=KernelMatrix(L4,'RBF_kernel',sig,L4);

%************************************************

A= [K1T+1/gamma*eye(m) , KL1T , KL2T, KL3T , KL4T , zeros((n-1)^2,1) ;....

    KL1T' , KL1L1' , KL2L1' , KL3L1' , KL4L1' , ones(n+1,1) ;...

    KL2T' , KL1L2' , KL2L2' , KL3L2' , KL4L2' , ones(n+1,1) ;...

    KL3T' , KL1L3' , KL2L3' , KL3L3' , KL4L3' , ones(n+1,1) ;...

    KL4T' , KL1L4' , KL2L4' , KL3L4' , KL4L4' , ones(n+1,1) ;...

    zeros((n-1)^2,1)' , ones(n+1,1)' , ones(n+1,1)' , ones(n+1,1)' , ones(n+1,1)' , 0 ];

B=[f(W(:,1),W(:,2)); L1(:,2).^3 ; (1+L2(:,2).^3)*exp(-1)  ;  L3(:,1).*exp(-L3(:,1)) ; exp(-L4(:,1)).*(L4(:,1)+1) ; 0 ];

result=A\B;

alpha=result(1:m);

beta1=result(m+1:m+n+1);

beta2=result(m+n+2:m+2*n+2);

beta3=result(m+2*n+3:m+3*n+3);

beta4=result(m+3*n+4:m+4*n+4);

b=result(end);

%% Result for training points

yhat= (Kxx' + Kyy')* alpha + KL1 * beta1 + KL2* beta2 + KL3* beta3 + KL4* beta4 +b;

yexa=@(p,q) exp(-p).*(p+q.^3);

yexact=yexa(W(:,1),W(:,2));

Error1= yexact- yhat;

MAX_Absolute_error_training=max(abs(yhat-yexact));

RMSE_training=sqrt(mse(yhat-yexact));

fprintf('-------  training set ------------------\n\n')

fprintf('Max Abs Error on training set=%d\n',MAX_Absolute_error_training)

fprintf('RMSE on training set=%d\n\n',RMSE_training)

subplot(2,3,2)

plot3(W(:,1),W(:,2),yhat,'pr')

hold all

plot3(W(:,1),W(:,2),yexact,'sb')

title('Approximate and exact solution for training points','Fontsize',14)

xlabel('x')

ylabel('y')

zlabel('u')

NError=reshape(Error1,size(X1,1),size(Y1,1));

Xn=linspace(0,1,n-1);

Yn=linspace(0,1,n-1);

subplot(2,3,3)

surface(Xn,Yn,NError)

shading interp

xlabel('y','Fontsize',14)

ylabel('x','Fontsize',14)

set(gca,'Fontsize',20)

grid on

h=colorbar;

set(h,'fontsize',14);

title('Absolute errors for training set','Fontsize',14)

%% Result for test points

a0=0;

b0=1;

n=31;

h=(b0-a0)/n;

[X2,Y2]=meshgrid(a0+h:h:b0-h);

WT=[];

for i=1:size(X2,2)

    Z=[X2(:,i),Y2(:,1)];

    WT=[WT ; Z];

end

subplot(2,3,4)

plot(WT(:,1),WT(:,2),'o')

title('Test points','Fontsize',14)

xlabel('x')

ylabel('y')

Kt=KernelMatrix(W,'RBF_kernel',sig,WT);

xt=WT(:,1);

yt=WT(:,2);

xx1t=x*ones(1,size(xt,1));

xx2t=xt*ones(1,size(x,1));

cof1t=-2*(xx1t-xx2t')/(sig);

xx3t=y*ones(1,size(yt,1));

xx4t=yt*ones(1,size(y,1));

cof2t=-2*(xx3t-xx4t')/(sig);

Ktestxx=(-2/sig)*Kt + (cof1t.^2) .* Kt;

Ktestyy=(-2/sig)*Kt + (cof2t.^2) .* Kt;

KKlte1=KernelMatrix(WT,'RBF_kernel',sig,L1);

KKlte2=KernelMatrix(WT,'RBF_kernel',sig,L2);

KKlte3=KernelMatrix(WT,'RBF_kernel',sig,L3);

KKlte4=KernelMatrix(WT,'RBF_kernel',sig,L4);

Ytest= (Ktestxx' + Ktestyy')* alpha + KKlte1 * beta1 + KKlte2* beta2 + KKlte3* beta3 + KKlte4* beta4 + b;

yextest=yexa(WT(:,1),WT(:,2));

subplot(2,3,5)

plot3(WT(:,1),WT(:,2),Ytest,'pr')

hold on

plot3(WT(:,1),WT(:,2),yextest,'sb')

title('Approximate and exact solution for test points','Fontsize',14)

xlabel('x')

ylabel('y')

zlabel('u')

yextest=yexa(WT(:,1),WT(:,2));

MAX_Absolute_error_test=max(abs(Ytest-yextest));

RMSE_test=sqrt(mse(Ytest-yextest));

fprintf('-------  test set ------------------\n\n')

fprintf('Max Abs Error on test set=%d\n',MAX_Absolute_error_test)

fprintf('RMSE on test set=%d\n\n',RMSE_test)

fprintf('-------  Finished -----------------------\n\n')

Error= Ytest - yextest ;

Ytnew=reshape(Ytest,size(X2,1),size(Y2,1));

Ytexa=reshape(yextest,size(X2,1),size(Y2,1));

NError=reshape(Error,size(X2,1),size(Y2,1));

Xn=linspace(0,1,n-1);

Yn=linspace(0,1,n-1);

subplot(2,3,6)

surface(Xn,Yn,NError)

shading interp

xlabel('y','Fontsize',14)

ylabel('x','Fontsize',14)

set(gca,'Fontsize',20)

grid on

h=colorbar;

set(h,'fontsize',14);

title('Absolute errors for test set','Fontsize',14)

🎉3 参考文献

[1] Mehrkanoon S., Falck T., Suykens J.A.K., "Approximate Solutions to Ordinary Differential Equations Using Least Squares Support Vector Machines",IEEE Transactions on Neural Networks and Learning Systems, vol. 23, no. 9, Sep. 2012, pp. 1356-1367.

[2] Mehrkanoon S., Suykens J.A.K.,"LS-SVM approximate solution to linear time varying descriptor systems", Automatica, vol. 48, no. 10, Oct. 2012, pp. 2502-2511.

[3] Mehrkanoon S., Suykens J.A.K., "Learning Solutions to Partial Differential Equations using LS-SVM",Neurocomputing, vol. 159, Mar. 2015, pp. 105-116.

👨‍💻4 Matlab代码 

http://www.yayakq.cn/news/75740/

相关文章：

  • 网站新备案不能访问沧州高端网站制作
  • 商务网站建设的应用惠州手机网站商城建设
  • 网站搜什么关键词好wordpress 客户端源码分析
  • 服务器方面如何规划建设网站梅河口信息网
  • 建设行政主管部门网站wordpress如何创建项目
  • ae模板下载网站电商企业网站建设
  • 公司网站在哪备案怎么做网页快
  • 学做网站 书怎样建设一个网站教学设计
  • 成都网站建设龙兵科技定制一个高端网站
  • 网站开发工程师 下载wordpress 上标 小圆1
  • 诸暨城乡与建设局网站福州网站建设营销q479185700刷屏
  • 乡林建设集团官方网站wordpress教程 菜单
  • 医院网站和微信公众号建设方案wordpress 页面固定
  • 设计师的网站南宁网站建设产品介绍
  • 百度推广还要求做网站电商seo引流
  • 免费送的广告怎么在网站上做自助下单网站咋做
  • 青岛网站优化价格浏览器怎么打开网站服务器下载
  • 域名只做邮箱没网站要备案吗asp 精品网站制作
  • 自己做的网站和ie不兼容网站开发的评论界面模板
  • 公司微信网站开发平台岗巴网站建设
  • 拓者吧室内设计网站如何选择医疗网站建设
  • 学校网站开发价格专题网站建设解决方案
  • 随州网站建设公司西安网站开发建
  • 做外汇的人一般看什么网站中小企业网络推广
  • 西安烽盈网站建设推广养老保险2023价格表
  • 网站开发 前端 后端 如何结合wordpress文章页调用
  • 做网站个体户经营范围什么是php网站开发
  • 大什么的网站建设公司生产许可证查询官网
  • 上传网站到google世界著名小型建筑设计
  • 网站设计模板免费下载个人网站界面设计图片