东莞专业网站建设公司sem优化托管公司
前言:
在之前的学习中,我们已经对初阶数据结构进行相应了学习,加上之前C语言的学习功底。今天,我们将会踏上更高一级“台阶”的学习-----即C++的学习!!!
文章目录
- 1.C++ 简介
- 1.1什么是C++
- 1.2.C++的发展史
- 2.C++关键字(C++98)
- 3. 命名空间
- 3.1命名空间定义
- 3.2 命名空间使用(重点)
- 4.C++输入&输出
- 5. 缺省参数
- 5.1 缺省参数概念
- 5.2 缺省参数分类
- 全缺省参数
- 半缺省参数
- 6. 函数重载
- 6.1 函数重载概念
- 6.2 C++支持函数重载的原理--名字修饰(name Mangling)
- 小结
1.C++ 简介
1.1什么是C++
在我们谈及C++的时候,不约而同的都会将其跟我们之前的C语言联系起来。那么我们学了这么久的C语言,大家知道C语言到底是什么嘛?对其的定义是否还了解呢?在不断的学习新知识下,我们记得要多加对之前学过的进行归纳总结哟
。废话不多说,我们回归正题,对之前学过的C语言是结构化和模块化的语言,适合处理较小规模的程序。对于复杂的问题,规模较大的程序,需要高度的抽象和建模时,C语言则不合适。为了解决软件危机, 20世纪80年代, 计算机界提出了OOP(object oriented programming:面向对象)思想,支持面向对象的程序设计语言应运而生 有了这一思想的铺垫,于是乎在1982年,BjarneStroustrup博士在C语言的基础上引入并扩充了面向对象的概念,发明了一种新的程序语言。为了表达该语言与C语言的渊源关系,命名为C++。因此:C++是基于C语言而产生的,它既可以进行C语言的过程化程序设计,又可以进行以抽象数据类型为特点的基于对象的程序设计,还可以进行面向对象的程序设计。
1.2.C++的发展史
在对C++有了基本的认识之后,作为一名资深的学习者,我们对C++的发展也需要进行相关了解。在1979年,贝尔实验室的本贾尼等人试图分析unix内核的时候,试图将内核模块化,于是在C语言的基础上进行扩展,增加了类的机制,完成了一个可以运行的预处理程序,称之为C with classes。
语言的发展就像是练功打怪升级一样,也是逐步递进,由浅入深的过程。我们先来看下C++的历史版本。

C++还在不断的向后发展。但是:现在公司主流使用还是C++98和C++11,所有大家不用追求最新,重点将C++98和C++11掌握好,等工作后,随着对C++理解不断加深,有时间可以去琢磨下更新的特性。
关于C++2X最新特性的讨论:
https://zhuanlan.zhihu.com/p/107360459
2.C++关键字(C++98)
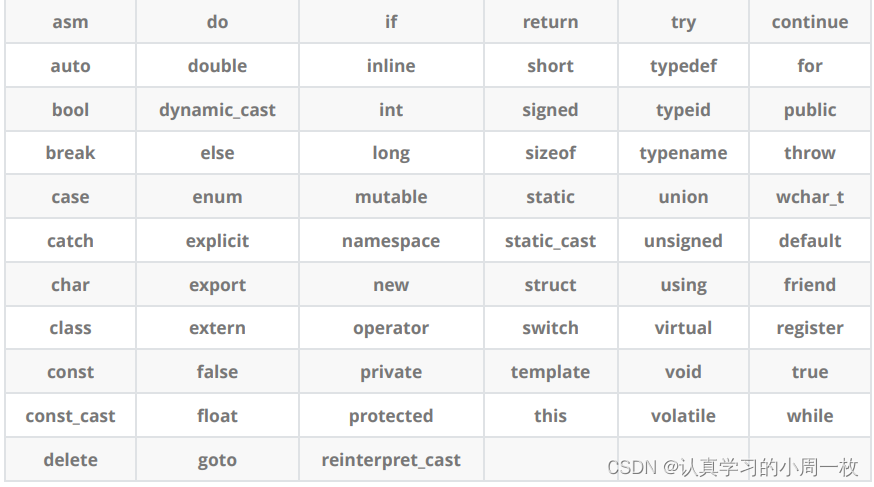
首先直接给出我们关键字的个数,大家对比C++和C语言的关键字的个数:
C++总计63个关键字,C语言32个关键字
我们不难发现,C++ 的关键字几乎是我们学习C语言时的一倍。大家不要被这表面现象所迷惑,在我们后面的学习中,我们会发现有很多的关键字我们在C语言时就已经学过了。
下面我们只是看一下C++有多少关键字,不对关键字进行具体的讲解。后面我们学到以后再细讲。
到这里或许有下伙伴会问,C语言的关键字到我们C++中难道会是一样的吗?开始时我们给出了C++的基本概念我们可以发现,C++是在我们C语言的基础上发明出来的,因此C++几乎是兼容我们的C语言的,我们通过一个例子来说明:
在我们开始学习C语言时,大家的第一个C语言程序大多就是【hello world】,那么在C++的环境下,程序是否还能跑起来呢?我们直接上代码:
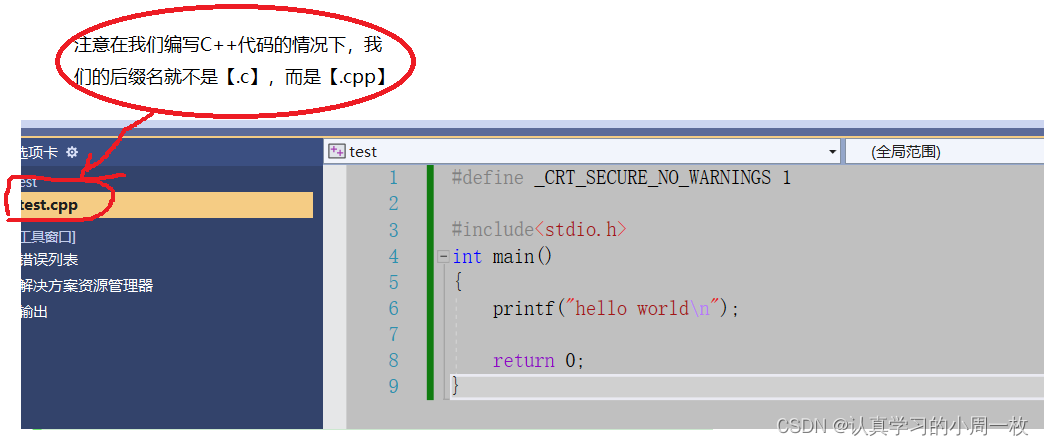
在我们进行编译的情况下,我们会发现程序依旧可以跑起来,并且会打印出相应的代码:


现在我们已经知道了C++兼容我们的C语言,那么如何使用我们C++的语法去进行代码的书写呢?我们还是以输出【hello world】为例,在C++的环境下,代码如下:
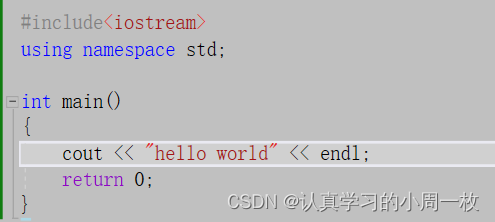
到这里就出现了很多新的知识,那么具体什么意思呢,我们对以上代码进行具体的解释:
1.C++ 语言定义了一些头文件,这些头文件包含了程序中必需的或有用的信息。上面这段程序中,包含了头文件 。
2.下一行 using namespace std; 告诉编译器使用 std 命名空间。命名空间是 C++ 中一个相对新的概念。
3.下一行 // main() 是程序开始执行的地方 是一个单行注释。单行注释以 // 开头,在行末结束。
4.下一行 int main() 是主函数,程序从这里开始执行。
5.下一行 cout << “Hello World”; 会在屏幕上显示消息 “Hello World”。
6.下一行 return 0; 终止 main( )函数,并向调用进程返回值 0。
3. 命名空间
在上述的代码详解中引入了一个【namespace】的概念因此,今天我们正式学习的第一个内容就是关于命名空间的有关知识。
那么命名空间到底是干什么的那?有什么作用呢引入这个概念,我们先对其进行文字理解:
在C/C++中,变量、函数和后面要学到的类都是大量存在的,这些变量、函数和类的名称将都存在于全局作用域中,可能会导致很多冲突。使用命名空间的目的是对标识符的名称进行本地化,以避免命名冲突或名字污染,namespace关键字的出现就是针对这种问题的。
有了对于文字的基本认识之后,大家脑袋里是不是云里雾里的呢?别急,我们还是通过代码一一的进行理解:
大家先看以下代码:
#include <stdio.h>
int rand = 10;
int main()
{printf("%d\n", rand);return 0;
}
以上代码在我们编译器的运行下是没有任何问题的:

但是当我们的加入头文件【#include <stdlib.h>】之后,我们的运行就会出现报错的情况:

在我们学习的过程中,我们知道库中有rand函数(取随机值),而我们却定义rand是一个变量 ,于是发生了命名冲突,这里就出现了报错跟我们库里面的函数重定义了。
#include <stdio.h>
#include <stdlib.h>
int rand = 10;
// C语言没办法解决类似这样的命名冲突问题,所以C++提出了namespace来解决
int main()
{printf("%d\n", rand);
return 0;
}
// 编译后后报错:error C2365: “rand”: 重定义;以前的定义是“函数”
如果大家还没理解,我们在举个例子,争取大家都能一次性吸收:
假设这样一种情况,当一个班上有两个名叫 【张三】的学生时,为了明确区分它们,我们在使用名字之外,不得不使用一些额外的信息,比如他们的身高,体重,或者他们父母的名字等等。
因此同样的情况也出现在 C++ 应用程序中。例如,您可能会写一个名为 xyz() 的函数,在另一个可用的库中也存在一个相同的函数 xyz()。这样,编译器就无法判断您所使用的是哪一个 xyz() 函数。
因此,引入了命名空间这个概念,专门用于解决上面的问题,它可作为附加信息来区分不同库中相同名称的函数、类、变量等。使用了命名空间即定义了上下文。本质上,命名空间就是定义了一个范围。
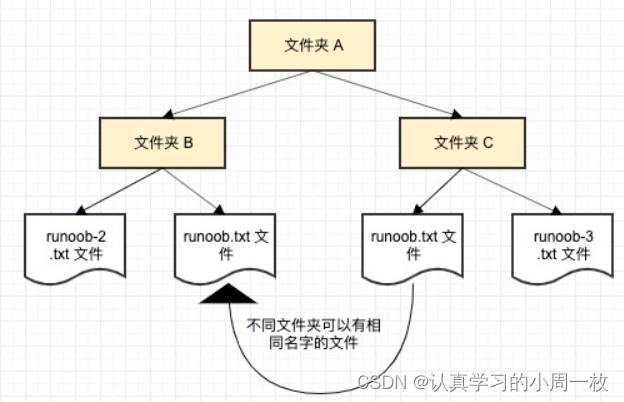
我们举一个计算机系统中的例子,一个文件夹(目录)中可以包含多个文件夹,每个文件夹中不能有相同的文件名,但不同文件夹中的文件可以重名。
3.1命名空间定义
定义命名空间,需要使用到namespace关键字,后面跟命名空间的名字,然后接一对{}即可,{}中即为命名空间的成员。
namespace namespace_name {// 代码声明
}
在正式的学习了解之前,先铺垫一个知识点,就是编译器有一套自己的查找变量的规则:
1.默认先去局部域找变量,局部域里面找不到后再去全局域里面去找变量
2.如果我们利用域作用限定符限定了编译器要查找的域,那编译器就会按照我们设定的查找规则来查找
老规矩我们还是通过相应的代码进行理解,大家先看以下代码:
#include <stdio.h>
// 局部域/全局域:1、使用 2、生命周期
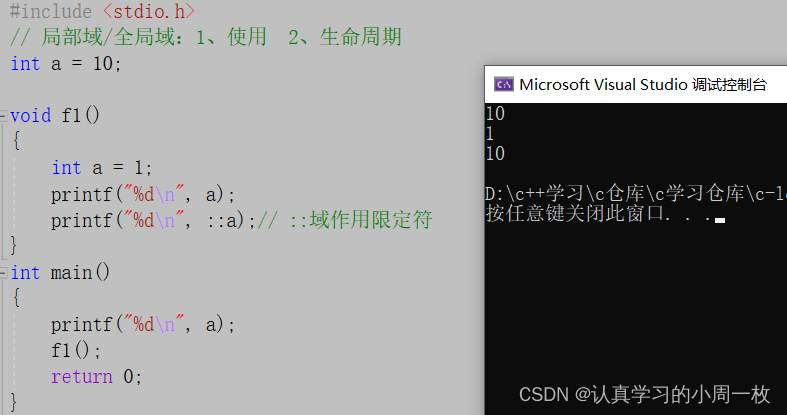
int a = 10;void f1()
{int a = 1; //定义在局部域中的参数变量printf("%d\n", a);printf("%d\n", ::a);// ::域作用限定符
}
int main()
{printf("%d\n", a);f1();return 0;
}根据相应的规则,我们可以进行相应的推理:
1.开始时我们定义了一个全局变量【a=10】,在主函数中的【a】毫无疑问打印出来的结果就是10;
2.在【void f1()】中我们又定义了一个a,此时的a为局部变量,即在作用内有效,出作用域就失效,因此,根据规则第一个打印的a应该就是局部变量中a的值,即1;
3.至于最后一个,在a之前加上了【::】符号,此时打印出来的结果仍是全局变量定义的a的值,即10.那么结果跟我们分析的是否一样呢?
有了上述的知识储备后,我们就来看看是如何定义命名空间的,接下来将会讲述三种情况:
a: 命名空间中可以定义变量/函数/类型
namespace zp // zp是命名空间的名字,一般开发中是用项目名字做命名空间名
{// 命名空间中可以定义变量/函数/类型int rand = 10;int Add(int left, int right){return left + right;}struct Node{struct Node* next;int val;};
}
b:命名空间可以嵌套定义
#include<iostream>
using namespace std;
namespace A
{int a = 1000;namespace B {int a = 2000;}
}
void test3()
{cout << "A中的a = " << A::a << endl; //1000cout << "B中的a = " << A::B::a << endl; //2000
}int main()
{test3();return 0;
}
一个命名空间当中又细分多个命名空间,这样也是可以的,代码空间当中就嵌套定义了A,N1中又嵌套定义了B。
c: 同一个工程中允许存在多个相同名称的命名空间,编译器最后会合成同一个命名空间中。
namespace A
{int a = 1000;
}
一个工程中的 A和上面的 A中两个 A会被合并成一个
注意:一个命名空间就定义了一个新的作用域,命名空间中的所有内容都局限于该命名空间中
3.2 命名空间使用(重点)
此时 我们已经知道了命名空间如何定义,那么接下来我们就得看一下命名空间如何使用了 。
我们依旧通过代码来进行举例,接下来,我们将看到以下代码:
#include<iostream>
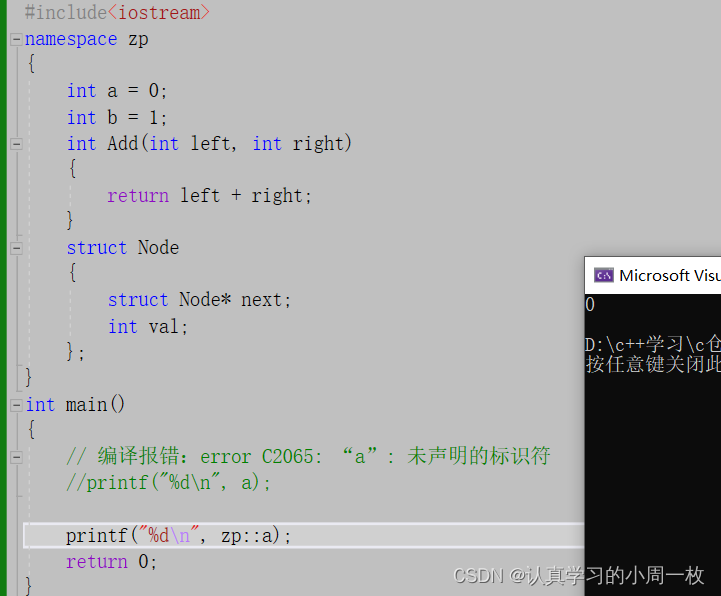
namespace zp
{int a = 0;int b = 1;int Add(int left, int right){return left + right;}struct Node{struct Node* next;int val;};
}
int main()
{// 编译报错:error C2065: “a”: 未声明的标识符printf("%d\n", a);return 0;
}
当我们运行上述代码时,就会出现报错的情况,具体如下:

那么我们如何解决这个问题呢?这就要引入命名空间使用的问题了,首先第一种:
a:加命名空间名称以及作用域限定符
int main()
{// 编译报错:error C2065: “a”: 未声明的标识符//printf("%d\n", a);printf("%d\n", zp::a);return 0;
}
我们不难发现,这种方式有相应的优缺点:
优点 : 指定访问,放需要用的命名空间中的变量到全局,不会导致命名污染
不足 : 代码量多的话,代码麻烦,代码冗杂, 不简洁
b:使用using将命名空间中某个成员引入
using zp::b;
int main()
{// 编译报错:error C2065: “a”: 未声明的标识符//printf("%d\n", a);printf("%d\n", zp::a);printf("%d\n", b);return 0;
}
运行结果如下:

优缺点分析:
优点 :放定义的变量到全局, 一次引用,多次调用,方便使用
不足 :如果调用命名空间内变量多的情况下,全局变量会增多
c:使用using namespace 命名空间名称 引入
int main()
{// 编译报错:error C2065: “a”: 未声明的标识符//printf("%d\n", a);//printf("%d\n", zp::a);//printf("%d\n", b);Add(10, 20);// 直接将命名空间zp中的Add函数引入return 0;
}
优缺点分析:
优点 :放全部变量到全局,便捷,只需声称一次命名空间
不足 :定义的变量多,有可能导致命名污染
std命名空间的使用惯例:
std是C++标准库的命名空间,如何展开std使用更合理呢?
- 在日常练习中,建议直接using namespace std即可,这样就很方便。
- using namespace std展开,标准库就全部暴露出来了,如果我们定义跟库重名的类型/对
象/函数,就存在冲突问题。该问题在日常练习中很少出现,但是项目开发中代码较多、规模
大,就很容易出现。所以建议在项目开发中使用,像std::cout这样使用时指定命名空间 +
using std::cout展开常用的库对象/类型等方式。
4.C++输入&输出
在C语言中,我们通常会使用 scanf 和 printf 来对数据进行输入输出操作。在C++语言中,C语言的这一套输入输出库我们仍然能使用,但是 C++ 又增加了一套新的、更容易使用的输入输出库。我们可以对比查看:

简单的输入输出代码示例:
#include<iostream>
using namespace std;int main()
{int x;float y;cout << "Please input an int number:" << endl;cin >> x;cout << "The int number is x= " << x << endl;cout << "Please input a float number:" << endl;cin >> y;cout << "The float number is y= " << y << endl;return 0;
}
运行结果如下(↙表示按下回车键):
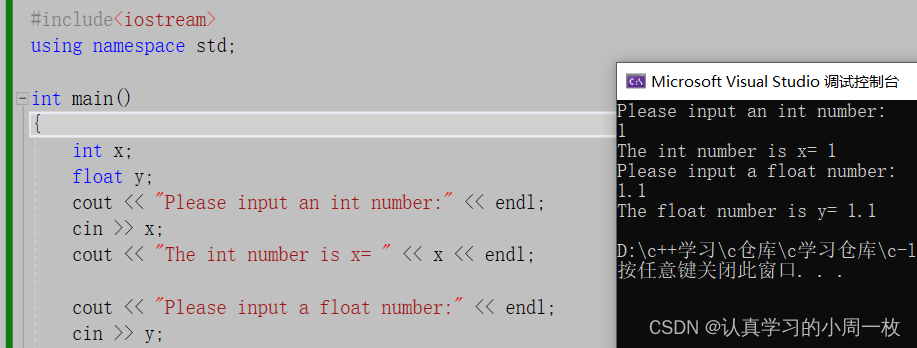
C++ 中的输入与输出可以看做是一连串的数据流,输入即可视为从文件或键盘中输入程序中的一串数据流,而输出则可以视为从程序中输出一连串的数据流到显示屏或文件中。
①
在编写 C++ 程序时,如果需要使用输入输出时,则需要包含头文iostream,它包含了用于输入输出的对象,例如常见的cin表示标准输入、cout表示标准输出、cerr表示标准错误。
iostream 是 Input Output Stream 的缩写,意思是“输入输出流”。
②
cout 和 cin 都是 C++ 的内置对象,而不是关键字。C++ 库定义了大量的类(Class),程序员可以使用它们来创建对象,cout 和 cin 就分别是 ostream 和 istream 类的对象,只不过它们是由标准库的开发者提前创建好的,可以直接拿来使用。这种在 C++ 中提前创建好的对象称为内置对象。
③
使用 cout 进行输出时需要紧跟<<运算符,使用 cin 进行输入时需要紧跟>>运算符,这两个运算符可以自行分析所处理的数据类型,因此无需像使用 scanf 和 printf 那样给出格式控制字符串。
④
代码表示输出"Please input a int number:"这样的一个字符串,以提示用户输入整数,其中endl表示换行,与C语言里的\n作用相同。当然这段代码中也可以用\n来替代endl,这样就得写作:
cout<<“Please input an int number:\n”;
特别注意:
endl 最后一个字符是字母“l”,而非阿拉伯数字“1”,它是“end of line”的缩写。
注意:早期标准库将所有功能在全局域中实现,声明在.h后缀的头文件中,使用时只需包含对应头文件即可,后来将其实现在std命名空间下,为了和C头文件区分,也为了正确使用命名空间,规定C++头文件不带.h;旧编译器(vc 6.0)中还支持<iostream.h>格式,后续编译器已不支持,因此推荐使用+std的方式。
#include <iostream>
using namespace std;
int main()
{int a;double b;char c;// 可以自动识别变量的类型cin>>a;cin>>b>>c;cout<<a<<endl;cout<<b<<" "<<c<<endl;return 0;
}
关于cout和cin还有很多更复杂的用法,比如控制浮点数输出精度,控制整形输出进制格式等。
我们在通过cin 连续输入示例来看看相关的用法:
#include<iostream>
using namespace std;
int main()
{int x;float y;cout << "Please input an int number and a float number:" << endl;cin >> x >> y;cout << "The int number is x= " << x << endl;cout << "The float number is y= " << y << endl;return 0;
}
运行结果如下:
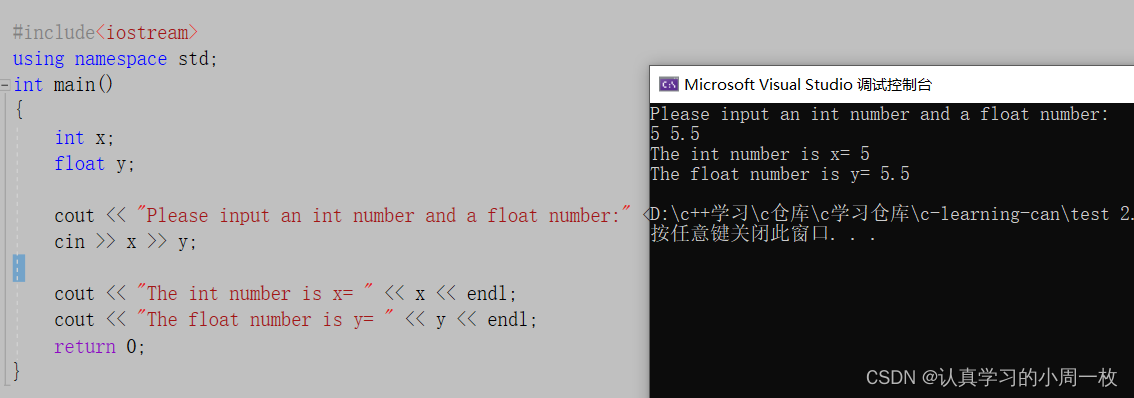
【cin>>】连续从标准输入中读取一个整型和一个浮点型数字(默认以空格分隔),分别存入到 x 和 y 中。
输入运算符>>在读入下一个输入项前会忽略前一项后面的空格,所以数字 5和 5.5之间要有一个空格,当 cin 读入 85后忽略空格,接着读取 5.5。
初学者可能会觉得 cout、cin 的用法非常奇怪,它们既不是类似 printf()、scanf()
的函数调用,也不是关键字,请大家先保留这个疑问,后续如果有需要,我 们再进行学习。
5. 缺省参数
5.1 缺省参数概念
缺省参数是声明或定义函数时为函数的参数指定一个缺省值。在调用该函数时,如果没有指定实参则采用该形参的缺省值,否则使用指定的实参。
缺省参数使用主要规则:
调用时你只能从最后一个参数开始进行省略,换句话说,如果你要省略一个参数,你必须省略它后面所有的参数,即:带缺省值的参数必须放在参数表的最后面。 缺省值必须是常量。
void Func(int a = 0)
{cout<<a<<endl;
}
int main()
{Func(); // 没有传参时,使用参数的默认值Func(10); // 传参时,使用指定的实参
return 0;
}
5.2 缺省参数分类
全缺省参数
顾名思义,全缺省就是参数的所有值都为缺省参数,如下代码所示:
void fun(int a = 1, int b = 2, int c = 3)
{cout << "a = " << a << endl;cout << "b = " << b << endl;cout << "c = " << c << endl;
}
int main()
{fun();fun(4, 5, 6);// fun(7, , 9); //报错return 0;
}
半缺省参数
半缺省指的是参数中有一部分为缺省参数,有一部分为非缺省参数。
值得注意的是,缺省参数只能为最右边的若干个。
void Func(int a, int b = 10, int c = 20)
{cout << "a = " << a << endl;cout << "b = " << b << endl;cout << "c = " << c << endl;
}int main()
{// Func(4, 5, 6);Func(7, ,9); //出现报错的情况return 0;
}

注意:
- 半缺省参数必须从右往左依次来给出,不能间隔着给
- 缺省参数不能在函数声明和定义中同时出现
- 缺省值必须是常量或者全局变量
- C语言不支持(编译器不支持)
总之记住,缺省参数只能为最右边的若干个参数。
6. 函数重载
在实际开发中,有时候我们需要实现几个功能类似的函数,只是有些细节不同。例如希望交换两个变量的值,这两个变量有多种类型,可以是 int、float、char、等,我们需要通过参数把变量的地址传入函数内部。在C语言中,程序员往往需要分别设计出三个不同名的函数,其函数原型与下面类似:
void swap1(int *a, int *b); //交换 int 变量的值
void swap2(float *a, float *b); //交换 float 变量的值
void swap3(char *a, char *b); //交换 char 变量的值
但在C++中,这完全没有必要。C++ 允许多个函数拥有相同的名字,只要它们的参数列表不同就可以,这就是函数的重载(Function Overloading)。借助重载,一个函数名可以有多种用途。
6.1 函数重载概念
函数重载:是函数的一种特殊情况,C++允许在同一作用域中声明几个功能类似的同名函数,这些同名函数的形参列表(参数个数 或 类型 或 类型顺序)不同,常用来处理实现功能类似数据类型不同的问题。
a:
重载声明是指一个与之前已经在该作用域内声明过的函数或方法具有相同名称的声明,但是它们的参数列表和定义(实现)不相同。
b:
当您调用一个重载函数或重载运算符时,编译器通过把您所使用的参数类型与定义中的参数类型进行比较,决定选用最合适的定义。选择最合适的重载函数或重载运算符的过程,称为重载决策。
当参数类型不同时:
// 1、参数类型不同
int Add(int left, int right)
{cout << "int Add(int left, int right)" << endl;return left + right;
}
double Add(double left, double right)
{cout << "double Add(double left, double right)" << endl;return left + right;
}
当参数个数不同时
// 2、参数个数不同
void f()
{cout << "f()" << endl;
}
void f(int a)
{cout << "f(int a)" << endl;
}
当类型顺序不同时
// 3、参数类型顺序不同
void f(int a, char b)
{cout << "f(int a,char b)" << endl;
}
void f(char b, int a)
{cout << "f(char b, int a)" << endl;
}
通过本例可以发现,重载就是在一个作用范围内(同一个类、同一个命名空间等)有多个名称相同但参数不同的函数。重载的结果是让一个函数名拥有了多种用途,使得命名更加方便(在中大型项目中,给变量、函数、类起名字是一件让人苦恼的问题),调用更加灵活。
在使用重载函数时,同名函数的功能应当相同或相近,不要用同一函数名去实现完全不相干的功能,虽然程序也能运行,但可读性不好,使人觉得莫名其妙。
注意,参数列表不同包括参数的个数不同、类型不同或顺序不同,仅仅参数名称不同是不可以的。函数返回值也不能作为重载的依据。
函数的重载的规则:
1.函数名称必须相同。
2.参数列表必须不同(个数不同、类型不同、参数排列顺序不同等)。
3.函数的返回类型可以相同也可以不相同。
4.仅仅返回类型不同不足以成为函数的重载。
然而当我们进行函数重载时,可能会出现一些差错行为,我们以如下代码为例:
#include <iostream>
using namespace std;void func(int, int);
void func(char, int, float);
void func(char, long, double); int main(){short n = 99;func('@', n, 99);func('@', n, 99.5); //二义性错误getchar();return 0;
}
上述代码函数确实构成函数重载,但在调用时,如果我们不指定实参的值,那就会产生二义性,编译器是不知道该调用哪个函数的,所以我们尽量不要写出这样的函数重载。
二义性是指编译器在寻找函数的时候不确定哪一个函数是正确的。类型重载函数存在二义性,因为编译器不能识别准确的函数,而只是比较参数类型来选择合适的重载函数。二义性常常是出现在参数类型相同的情况下,参数的数量不同,有可能会让编译器无法识别函数从而出现错误。
因此,在C++中,函数重载可能会出现二义性和类型转换的问题,所以我们在使用重载函数时要分清楚函数的参数个数和类型,进而确保重载函数正确定义并使用。
6.2 C++支持函数重载的原理–名字修饰(name Mangling)
在C/C++中,一个程序要运行起来,需要经历以下几个阶段:预处理、编译、汇编、链接。 实际项目通常是由多个头文件和多个源文件构成,而通过C语言阶段学习的编译链接,我们可以知道,【当前a.cpp中调用了b.cpp中定义的Add函数时】编译后链接前,a.obj的目标文件中没有Add的函数地址,因为Add是在b.cpp中定义的,所以Add的地址在b.obj中。那么怎么办 链接器看到a.obj调用Add,但是没有Add的地址,就会到b.obj的符号表中找Add的地址,然后链接到一起。
在编译结束之后,a.cpp和b.cpp都会产生目标文件.obj,每个目标文件中都会有他们自己的符号表,汇总了全局域里面的函数名,变量名,结构体名等等
那么链接时,面对Add函数,链接接器会使用哪个名字去找呢?这里每个编译器都有自己的函数名修饰规则。
下面我们使用了g++演示了这个修饰后的名字
①
采用C语言编译器编译后结果:
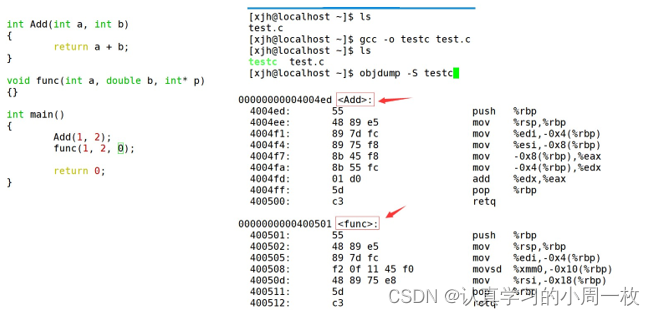
结论:在linux下,采用gcc编译完成后,函数名字的修饰没有发生改变。
②
采用C++编译器编译后结果
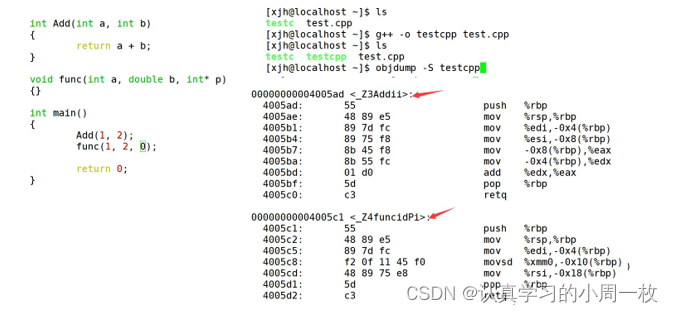
结论:在linux下,采用g++编译完成后,函数名字的修饰发生改变,编译器将函数参数类型信息添加到修改后的名字中。
通过这里就理解了C语言没办法支持重载,因为同名函数没办法区分。而C++是通过函数修饰规则来区分,只要参数不同,修饰出来的名字就不一样,就支持了重载。
小结
至此,我们对C++的学习旅程便开启了,总所周知,C++的学习是相对来说较难的。那么我们自己怎么学号C++呢?我认为可以从以下几个方面入手:
a:多总结。对比学习过的知识,我们要多进行归纳总结,通过自己的梳理,让大脑有了完整性的知识框架;
b:多看书。合理的看书安排,切记贪,缓缓图之,否则容易走火入魔。入门阶段,找一本简单、薄一点的书快速入门,《C++程序设计》就挺适合的,可以简单快速了解C++的语法特性;
c:最后就是多刷题啦!做题是对知识掌握程度最直接的检验。
