成都建设网站哪家好wordpress 应用

凡事都有可能，永远别说永远。——《放牛班的春天》

今天一题为再一个行列都有序的二维数组中寻找一个目标值，我们第一时间想到的可能是很暴力的解法，例如从头到尾进行遍历，这样能做出来，但是借用武忠祥老师的一句话：这样做你就慢了，没效率。

本文章会从复杂度的角度来分析一个算法，循序渐进的提升这个算法的优秀程度。最终优化为最优算法。

一.题目及示例

在一个二维数组array中（每个一维数组的长度相同），每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

[
[1,2,8,9],
[2,4,9,12],
[4,7,10,13],
[6,8,11,15]
]
给定 target = 7，返回 true。
给定 target = 3，返回 false。

下面给出示例：

解法一(暴力解法)：

拿到这道题目，第一种方法不难想到，就是对整个数组进行遍历，每一个元素都扫一遍。这种解法比较暴躁，很暴力，给它一个外号，叫"暴力解法"。

具体代码实现如下：

bool Find(int target, vector<vector<int> > array) {// 利用C++的auto进行遍历for(auto x:array) {for(auto y:x){// 如果存在，直接返回trueif(y==target){return true;}}}return false;

ps:这里的for循环不是普通的for循环，这是C++新定义的for循环，具体使用可以去看我下一篇博客。

我把他称之为升级版for循环。

复杂度分析：

• 需要对二维数组的每个元素进行遍历，时间复杂度为O(n^2)

• 存储一个二维数组，空间复杂度为O(1)

解法二(双指针法)

由于矩阵行列都是严格递增的，此矩阵为杨氏矩阵，故也称杨氏矩阵法。

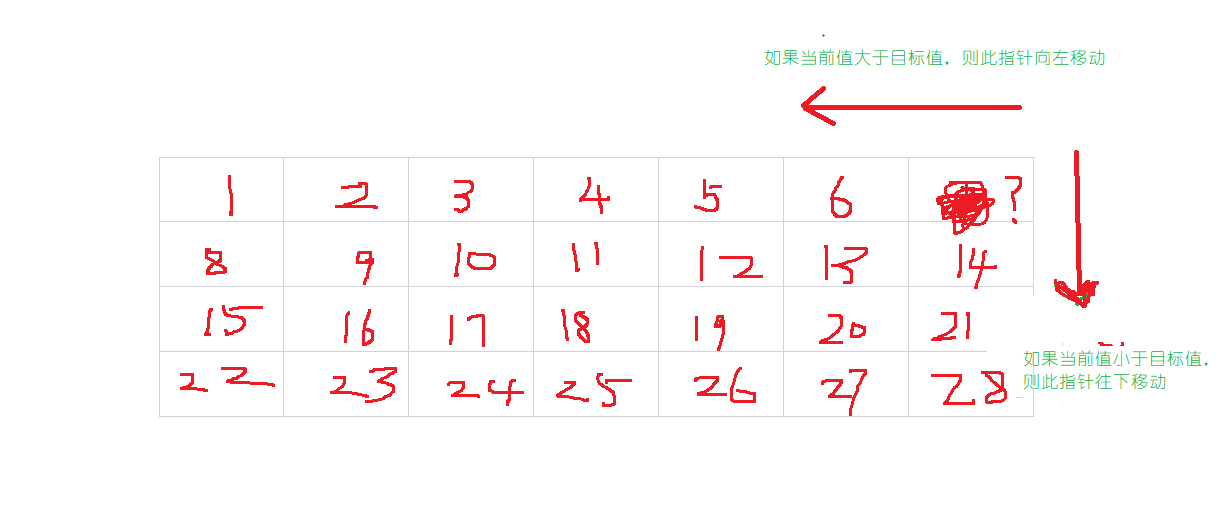
• 如果这个是一个没有任何规律的数组，那么可能就只有那种写法了，但是这个题目(红字)告诉我们这个数字从上到下，从左到右都是递增的，所以我们可以从这个方向入手。我们发现，我们找一个数，最快的办法无非就是利用二分进行查找，但是我们发现这个题目是一个二维单调的。所以我们要想办法找到一个方法可以在我们判断到数字小了或者大了的时候可以进行一个范围的缩小。这样的话，我们就可以定义两个指针，放到右上角或者左下角。这里我放到右上角进行讨论。
  初始的时候，我们的两个x和y的指针放到了右上角。这样的话我们可以与目标数进行比较，如果发现这个数比目标数小了，我们就把y指针往下进行移动，y指针自增。如果发现这个数比目标数大了，我们就可以往左边方向进行移动，x指针自减。

具体代码实现如下：

（右上角代码）

 bool Find(int target, vector<vector<int> > array) {int len1=array.size();  // 计算行数int len2=array[0].size();  //计算列数int posx=0,posy=len2-1; //定义两个指针，分别指向x和y的坐标while(posx<len1&&posy>=0){// 当前的数字比目标数字大，x指针左移if(array[posx][posy]>target){posy--;// 当前的数字比目标数字小，y指针往下移动}else if(array[posx][posy]<target){posx++;}else{return true;}}return false;}

(左下角代码)

bool Find(int target, vector<vector<int> > array) {int len1=array.size(); // 行数int len2=array[0].size();  //列数int posx=len1-1,posy=0; // 定义两个指针，分别表示x和y的指针while(posx>=0&&posy<len2){// 当前的数字比目标数字大，x指针往上移动if(array[posx][posy]>target){posx--;// 当前的数字比目标数字小，y指针往右方向移动}else if(array[posx][posy]<target){posy++;}else{return true;}}return false;}

复杂度分析：

由于x和y分别只能往一个方向进行移动。

• 右上角版,最有最多只会遍历一行和一列的长度，时间复杂度为O(n+m)

• 二维数组存储所有的元素，空间的复杂度为O(1)

我们做个总结，相对于第一题，第二题的时间复杂度从n^2到m+n得到提升，提升的原因就是很好的利用升序这个特点来优化。