做贷款的网站佛山网站建设企业
安全配置
说明:IP地址按照题目给定的顺序用“ip/mask”表示,IPv4 any地址用0.0.0.0/0,IPv6 any地址用::/0,禁止用地址条目,否则按零分处理。
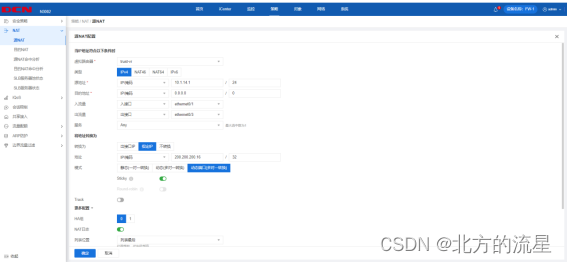
1.FW1配置IPv4 nat,实现集团产品1段IPv4访问Internet IPv4,转换ip/mask为200.200.200.16/28,保证每一个源IP产生的所有会话将被映射到同一个固定的IP地址;当有流量匹配本地址转换规则时产生日志信息,将匹配的日志发送至10.10.11.99的 UDP 514端口,记录主机名,用明文轮询方式分发日志;开启相关特性,实现扩展nat转换后的网络地址端口资源。