青海网站开发多少钱搜狗官网
随着科技的不断发展,设备巡检工作也在逐步向智能化、高效化方向转变。传统的巡检方式往往需要人工逐个设备检查,耗时耗力,效率低下,同时还容易漏检和误检。而新型设备巡检应用—手机蓝牙云巡检的出现,则为设备巡检工作带来了全新的变革。
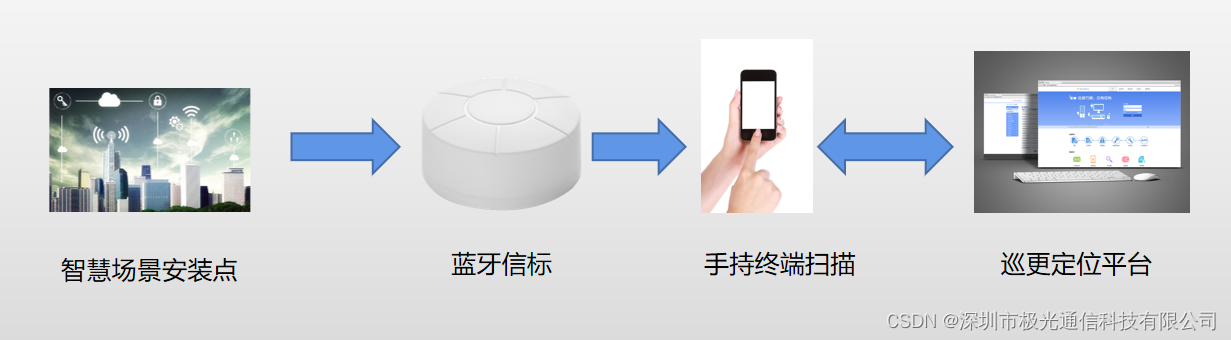
手机蓝牙云巡检是一种基于蓝牙信标技术和云计算的设备巡检应用,蓝牙信标安装于设备上,手机与蓝牙信标连接,实现巡检数据的实时采集、传输和处理。该应用具有高效、便捷、智能等特点,能够大大提高巡检工作的效率和质量。
首先,手机蓝牙云巡检具有高效性。传统的巡检方式需要巡检人员逐个设备检查,而手机蓝牙云巡检则可以通过蓝牙技术自动扫描蓝牙信标,快速获取设备信息,大大缩短了巡检时间。同时,该应用还可以实现数据的实时传输和处理,使得巡检数据能够即时反馈到管理人员手中,帮助他们及时发现问题并进行处理。
其次,手机蓝牙云巡检具有便捷性。传统的巡检方式需要巡检人员携带大量的巡检工具和设备,而手机蓝牙云巡检则只需要一部手机就可以完成所有的巡检工作。巡检人员可以随时随地进行巡检,无需担心遗漏或错过设备。同时,该应用还支持多种巡检模式,可以根据不同的巡检需求进行灵活配置,使得巡检工作更加便捷。
最后,手机蓝牙云巡检具有智能性。该应用可以通过数据分析和算法优化,对设备状态进行智能预测和预警,帮助管理人员及时发现潜在问题并采取相应的措施。同时,该应用还支持远程控制和监控,可以实现对设备的远程管理和维护,提高了设备管理的智能化水平。
总之,手机蓝牙云巡检作为一种新型的设备巡检应用,具有高效、便捷、智能等特点,能够大大提高巡检工作的效率和质量。它的出现不仅改变了传统巡检方式的局限性,也为设备巡检工作带来了全新的变革。未来,随着科技的不断进步和应用场景的不断拓展,手机蓝牙云巡检将会在更多的领域得到应用和推广,为人们的生活和工作带来更多的便利和效益。
在实际应用中,手机蓝牙云巡检不仅可以应用于各种设备的巡检工作,还可以结合其他技术,如物联网、大数据等,实现更加智能化的设备管理和维护。例如,通过物联网技术,可以将设备与云平台连接起来,实现设备的远程监控和控制;通过大数据技术,可以对巡检数据进行深度分析和挖掘,发现潜在的问题和规律,为设备的维护和管理提供更加科学的依据。
同时,手机蓝牙云巡检还具有广泛的应用前景。在工业生产领域,该应用可以用于各种设备的巡检和维护,提高生产效率和设备可靠性;在智慧城市建设中,该应用可以用于公共设施和交通设备的巡检和管理,提升城市管理和服务水平;在医疗卫生领域,该应用可以用于医疗设备的巡检和维护,保障医疗设备的正常运行和患者的安全。
总之,手机蓝牙云巡检作为一种新型的设备巡检应用,具有广泛的应用前景和巨大的发展潜力。它的出现将为设备巡检工作带来更加高效、便捷和智能的解决方案,推动设备管理和维护工作的不断升级和发展。
蓝牙信标参数
产品品牌:极光通信
产品尺寸:53.86*24.93mm
安装方式:3M胶或螺钉或者扎带
防水等级:IP65或IP68
通讯协议:BLE4.2或BLE5.0
外壳材质:PC
外壳颜色:白色
传输距离:100米
可修改的参数:可修改参数:设备名称、UUID、发射功率、广播间隔、Major、Minor、连接密码