锡林浩特市长安网站 建设初步方案广西柳州网站建设公司
目录
- pom引用
- java bean 类
- XML 转换工具类
- 测试类
- 执行结果
- 注意问题
JAXB方式见:
JAXB实现XML和Bean相互转换
Java中实现XML和Bean的转换的方式或插件有以下几种:
JAXB(Java Architecture for XML Binding):JAXB是Java SE的一部分,可以将Java对象与XML文档相互转换。它提供了注解和XML绑定文件两种配置方式。
Dom4j:Dom4j是一个开源的Java库,用于操作XML文档。它可以将XML文档转换为Java对象,也可以将Java对象转换为XML文档。
XStream:XStream是一个简单易用的Java库,用于序列化和反序列化对象。它可以将Java对象转换为XML文档,也可以将XML文档转换为Java对象。
SimpleXML:SimpleXML是一个轻量级的Java库,用于处理XML文档。它可以将XML文档转换为Java对象,也可以将Java对象转换为XML文档。
Jackson:Jackson是一个流行的Java库,用于处理JSON数据。它也支持将Java对象转换为XML文档,以及将XML文档转换为Java对象。
JiBX:JiBX是一个强大的Java库,用于处理XML文档。它可以将Java对象与XML文档相互转换,支持多种映射策略。
Castor:Castor是一个高性能的Java库,用于处理XML文档。它可以将Java对象与XML文档相互转换,支持多种映射策略。
Apache CXF:Apache CXF是一个开源的Web服务框架,提供了许多用于处理XML和SOAP消息的功能。它支持将Java对象与XML文档相互转换。
这里介绍一下 XStream。
pom引用
<dependency><groupId>com.thoughtworks.xstream</groupId><artifactId>xstream</artifactId><version>1.4.20</version></dependency>
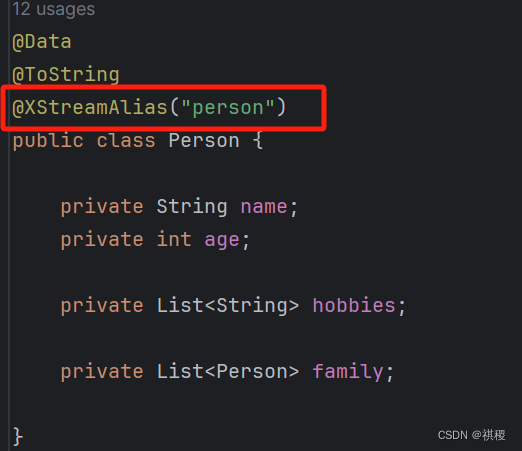
java bean 类
import com.thoughtworks.xstream.annotations.XStreamAlias;
import lombok.Data;
import lombok.ToString;import java.util.List;@Data
@ToString
@XStreamAlias("person")
public class Person {private String name;private int age;private List<String> hobbies;private List<Person> family;}
XML 转换工具类
import com.thoughtworks.xstream.XStream;
import com.thoughtworks.xstream.io.xml.DomDriver;
import com.thoughtworks.xstream.security.AnyTypePermission;
import lombok.extern.slf4j.Slf4j;@Slf4j
public class XMLUtil {private XMLUtil() {}public static Object convertFromXML(Class<?> clazz, String xml) {XStream xStream = new XStream(new DomDriver());// 避免 com.thoughtworks.xstream.security.ForbiddenClassException异常xStream.addPermission(AnyTypePermission.ANY);// 处理注解xStream.processAnnotations(clazz);// 将XML字符串转为bean对象return xStream.fromXML(xml);}public static String convertToXml(Object obj) {XStream xs = new XStream(new DomDriver());xs.processAnnotations(obj.getClass());return xs.toXML(obj);}
}
测试类
import org.junit.jupiter.api.Test;
import org.springframework.boot.test.context.SpringBootTest;
import will.tools.model.Person;
import will.tools.util.XMLUtil;import java.util.ArrayList;
import java.util.List;@SpringBootTest
public class XMLUtilTests {@Testpublic void test() {Person p2 = getPerson();String xml = XMLUtil.convertToXml(p2);System.out.println("对象转xml");System.out.println(xml);// String xml =
//
// "<person>\n" +
// " <name>黄蓉</name>\n" +
// " <age>18</age>\n" +
// " <hobbies>\n" +
// " <string>sing</string>\n" +
// " <string>dance</string>\n" +
// " </hobbies>\n" +
// " <family>\n" +
// " <person>\n" +
// " <name>郭靖</name>\n" +
// " <age>20</age>\n" +
// " <hobbies>\n" +
// " <string>射箭</string>\n" +
// " <string>爬山</string>\n" +
// " </hobbies>\n" +
// " </person>\n" +
// " </family>\n" +
// "</person>";Person p = (Person) XMLUtil.convertFromXML(Person.class, xml);System.out.println("xml转对象");System.out.println(p.toString());}private static Person getPerson() {Person p1 = new Person();p1.setAge(20);p1.setName("郭靖");List<String> lst = new ArrayList<>();lst.add("射箭");lst.add("爬山");p1.setHobbies(lst);Person p2 = new Person();p2.setAge(18);p2.setName("黄蓉");List<String> hobbyList = new ArrayList<>();hobbyList.add("sing");hobbyList.add("dance");p2.setHobbies(hobbyList);List<Person> list = new ArrayList<>();list.add(p1);p2.setFamily(list);return p2;}
}
执行结果
对象转xml
<person><name>黄蓉</name><age>18</age><hobbies><string>sing</string><string>dance</string></hobbies><family><person><name>郭靖</name><age>20</age><hobbies><string>射箭</string><string>爬山</string></hobbies></person></family>
</person>xml转对象Person(name=黄蓉, age=18, hobbies=[sing, dance], family=[Person(name=郭靖, age=20, hobbies=[射箭, 爬山], family=null)])
注意问题
1、xml转bean时报错:com.thoughtworks.xstream.security.ForbiddenClassException: will.tools.model.Person
解决方法:
增加 该属性设置:xStream.addPermission(AnyTypePermission.ANY);
代码中已增加。
2、bean转换xml时,转换为类名
<will.tools.model.Person>
…
…
</will.tools.model.Person>
使用别名
XMLUtil源文件下载 无需积分:
XMLUtil下载
