女装网站建设的规划书上海做外贸网站设计
文章目录
- 一、Redis 高可用:
- 1.简介:
- 2、在Redis中实现高可用的技术
- 二、Redis持久化:
- 1.持久化的功能:
- 2.Redis 提供两种方式进行持久化:
- 三、RDB 持久化:
- 1.简介:
- 2.触发条件:
- 4.启动时加载:
- 5.RDB的优缺点:
- 四、AOF 持久化:
- 1.开启AOF:
- 2.执行流程:
- 3.启动时加载:
- 4.AOF的优缺点:
- 五、Redis 性能管理:
- 1.查看Redis内存使用:
- 2.内存碎片率:
- 3.内存使用率:
- 4.内回收key:
- 六、RDB和AOF的总结:
- 1.RDB和AOF的基本理解:
- 2.RDB和AOF持久化的过程:
- 3.RDB和AOF的触发方式:
- 4.RDB和AOE优先级:
- 5.RDB和AOF的优缺点:
一、Redis 高可用:
1.简介:
在web服务器中,高可用是指服务器可以正常访问的时间,衡量的标准是在多长时间内可以提供正常服务(99.9%、99.99%、99.999%等等)。
在Redis语境中,高可用的含义似乎要宽泛一些,除了保证提供正常服务(如主从分离、快速容灾技术),还需要考虑数据容量的扩展、数据安全不会丢失等。
2、在Redis中实现高可用的技术
主要包括持久化、主从复制、哨兵和 Cluster集群
持久化:持久化是最简单的高可用方法(有时甚至不被归为高可用的手段),主要作用是数据备份,即将数据存储在硬盘,保证数据不会因进程退出而丢失。
主从复制:主从复制是高可用Redis的基础,哨兵和集群都是在主从复制基础上实现高可用的。主从复制主要实现了数据的多机备份,以及对于读操作的负载均衡和简单的故障恢复。缺陷:故障恢复无法自动化;写操作无法负载均衡;存储能力受到单机的限制。
哨兵:在主从复制的基础上,哨兵实现了自动化的故障恢复。缺陷:写操作无法负载均衡;存储能力受到单机的限制。
Cluster集群:通过集群,Redis解决了写操作无法负载均衡,以及存储能力受到单机限制的问题,实现了较为完善的高可用方案。
二、Redis持久化:
1.持久化的功能:
Redis是内存数据库,数据都是存储在内存中,为了避免服务器断电等原因导致Redis进程异常退出后数据的永久丢失,需要定期将Redis中的数据以某种形式(数据或命令)从内存保存到硬盘;当下次Redis重启时,利用持久化文件实现数据恢复。除此之外,为了进行灾难备份,可以将持久化文件拷贝到一个远程位置。
2.Redis 提供两种方式进行持久化:
(1)RDB 持久化:原理是将 Reids在内存中的数据库记录定时保存到磁盘上。
(2)AOF 持久化(append only file):原理是将 Reids 的操作日志以追加的方式写入文件,类似于MySQL的binlog。
由于AOF持久化的实时性更好,即当进程意外退出时丢失的数据更少,因此AOF是目前主流的持久化方式,不过RDB持久化仍然有其用武之地。
三、RDB 持久化:
1.简介:
RDB持久化是指在指定的时间间隔内将内存中当前进程中的数据生成快照保存到硬盘(因此也称作快照持久化),用二进制压缩存储,保存的文件后缀是rdb;当Redis重新启动时,可以读取快照文件恢复数据。
2.触发条件:
RDB持久化的触发分为手动触发和自动触发两种。
(1)手动触发:
save命令和bgsave命令都可以生成RDB文件。
save命令会阻塞Redis服务器进程,直到RDB文件创建完毕为止,在Redis服务器阻塞期间,服务器不能处理任何命令请求。
而bgsave命令会创建一个子进程,由子进程来负责创建RDB文件,父进程(即Redis主进程)则继续处理请求。
bgsave命令执行过程中,只有fork子进程时会阻塞服务器,而对于save命令,整个过程都会阻塞服务器,因此save已基本被废弃,线上环境要杜绝save的使用。
(2)自动触发:
在自动触发RDB持久化时,Redis也会选择bgsave而不是save来进行持久化。
save m n
自动触发最常见的情况是在配置文件中通过save m n,指定当m秒内发生n次变化时,会触发bgsave。
vim /etc/redis/6379.conf
--219行--以下三个save条件满足任意一个时,都会引起bgsave的调用
save 900 1 :当时间到900秒时,如果redis数据发生了至少1次变化,则执行bgsave
save 300 10 :当时间到300秒时,如果redis数据发生了至少10次变化,则执行bgsave
save 60 10000 :当时间到60秒时,如果redis数据发生了至少10000次变化,则执行bgsave
--254行--指定RDB文件名
dbfilename dump.rdb
--264行--指定RDB文件和AOF文件所在目录
dir /var/lib/redis/6379
--242行--是否开启RDB文件压缩
rdbcompression yes
(3)其他自动触发机制:
除了save m n 以外,还有一些其他情况会触发bgsave:
① 在主从复制场景下,如果从节点执行全量复制操作,则主节点会执行bgsave命令,并将rdb文件发送给从节点。
② 执行shutdown命令时,自动执行rdb持久化。
3.执行流程:
(1)Redis父进程首先判断:当前是否在执行save,或bgsave/bgrewriteaof的子进程,如果在执行则bgsave命令直接返回。bgsave/bgrewriteaof的子进程不能同时执行,主要是基于性能方面的考虑:两个并发的子进程同时执行大量的磁盘写操作,可能引起严重的性能问题。
(2)父进程执行fork操作创建子进程,这个过程中父进程是阻塞的,Redis不能执行来自客户端的任何命令
(3)父进程fork后,bgsave命令返回”Background saving started”信息并不再阻塞父进程,并可以响应其他命令
(4)子进程创建RDB文件,根据父进程内存快照生成临时快照文件,完成后对原有文件进行原子替换
(5)子进程发送信号给父进程表示完成,父进程更新统计信息

4.启动时加载:
RDB文件的载入工作是在服务器启动时自动执行的,并没有专门的命令。但是由于AOF的优先级更高,因此当AOF开启时,Redis会优先载入。
AOF文件来恢复数据;只有当AOF关闭时,才会在Redis服务器启动时检测RDB文件,并自动载入。服务器载入RDB文件期间处于阻塞状态,直到载入完成为止。
Redis载入RDB文件时,会对RDB文件进行校验,如果文件损坏,则日志中会打印错误,Redis启动失败。
5.RDB的优缺点:
优点:
① 持久化速度块(因为保存的数据结果),在写入到*.rdb持久化文件进行压缩,来减小自身的体积
② 集群中,redis主从复制,从——主服务器进行同步,默认先使用RDB文件进行,恢复操作,所有同步性能较高
缺点:
① 数据完整性不如aof
② rdb类似快照(完善)
③ 在进行备份时,会阻塞进程
四、AOF 持久化:
RDB持久化是将进程数据写入文件,而AOF持久化,则是将Redis执行的每次写、删除命令记录到单独的日志文件中,查询操作不会记录; 当Redis重启时再次执行AOF文件中的命令来恢复数据。与RDB相比,AOF的实时性更好,因此已成为主流的持久化方案。
1.开启AOF:
Redis服务器默认开启RDB,关闭AOF;要开启AOF,需要在配置文件中配置:
vim /etc/redis/6379.conf
--700行--修改,开启AOF
appendonly yes
--704行--指定AOF文件名称
appendfilename "appendonly.aof"
--796行--是否忽略最后一条可能存在问题的指令
aof-load-truncated yes
/etc/init.d/redis_6379 restart
2.执行流程:
由于需要记录Redis的每条写命令,因此AOF不需要触发,AOF的执行流程如下。
命令追加(append) :
① Redis先将写命令追加到缓冲区,而不是直接写入文件,主要是为了避免每次有写命令都直接写入硬盘,导致硬盘IO成为Redis负载的瓶颈。
② 命令追加的格式是Redis命令请求的协议格式,它是一种纯文本格式,具有兼容性好、可读性强、容易处理、操作简单避免二次开销等优点。
③ 在AOF文件中,除了用于指定数据库的select命令(如select 0为选中0号数据库)是由Redis添加的,其他都是客户端发送来的写命令。
文件写入(write)和文件同步(sync):
Redis提供了多种AOF缓存区的同步文件策略,策略涉及到操作系统的write函数和fsync函数,说明如下:
为了提高文件写入效率,在现代操作系统中,当用户调用write函数将数据写入文件时,操作系统通常会将数据暂存到一个内存缓冲区里,当缓冲区被填满或超过了指定时限后,才真正将缓冲区的数据写入到硬盘里。这样的操作虽然提高了效率,但也带来了安全问题:如果计算机停机,内存缓冲区中的数据会丢失;因此系统同时提供了fsync、fdatasync等同步函数,可以强制操作系统立刻将缓冲区中的数据写入到硬盘里,从而确保数据的安全性。
AOF缓存区的同步文件策略存在三种同步方式,它们分别是:
vim /etc/redis/6379.conf
--729--
●appendfsync always: 命令写入aof_buf后立即调用系统fsync操作同步到AOF文件,fsync完成后线程返回。这种情况下,每次有写命令都要同步到AOF文件,硬盘IO成为性能瓶颈,Redis只能支持大约几百TPS写入,严重降低了Redis的性能;即便是使用固态硬盘(SSD),每秒大约也只能处理几万个命令,而且会大大降低SSD的寿命。●appendfsync no: 命令写入aof_buf后调用系统write操作,不对AOF文件做fsync同步;同步由操作系统负责,通常同步周期为30秒。这种情况下,文件同步的时间不可控,且缓冲区中堆积的数据会很多,数据安全性无法保证。●appendfsync everysec: 命令写入aof_buf后调用系统write操作,write完成后线程返回;fsync同步文件操作由专门的线程每秒调用一次。everysec是前述两种策略的折中,是性能和数据安全性的平衡,因此是Redis的默认配置,也是我们推荐的配置。文件重写(rewrite)
① 文件重写是指定期重写AOF文件,减小AOF文件的体积。需要注意的是,AOF重写是把Redis进程内的数据转化为写命令,同步到新的AOF文件,不会对旧的AOF文件进行任何读取、写入操作!
② 关于文件重写需要注意的另一点是:对于AOF持久化来说,文件重写虽然是强烈推荐的,但并不是必须的;即使没有文件重写,数据也可以被持久化并在Redis启动的时候导入;因此在一些现实中,会关闭自动的文件重写,然后通过定时任务在每天的某一时刻定时执行。
③ 文件重写之所以能够压缩AOF文件,原因在于:
过期的数据不再写入文件
无效的命令不再写入文件:如有些数据被重复设值(set mykey v1, set mykey v2)、有些数据被删除了(set myset v1, del myset)等。
多条命令可以合并为一个:如sadd myset v1, sadd myset v2, sadd myset v3可以合并为sadd myset v1 v2 v3。
通过上述内容可以看出,由于重写后AOF执行的命令减少了,文件重写既可以减少文件占用的空间,也可以加快恢复速度。
④ 文件重写的触发,分为手动触发和自动触发:
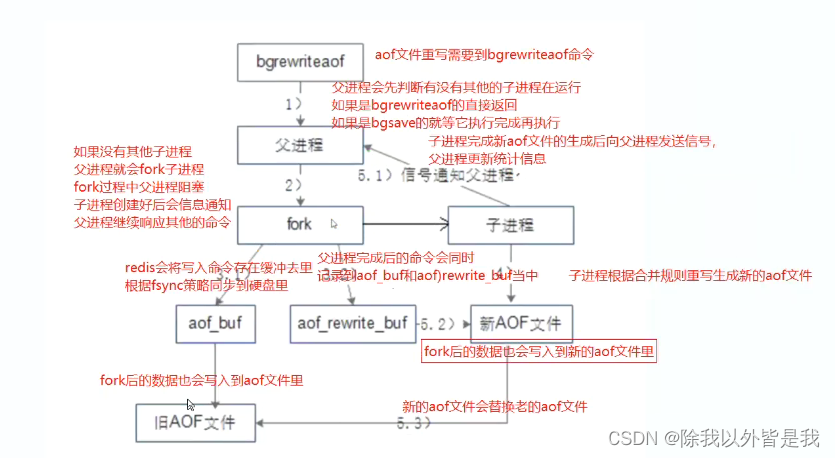
手动触发:直接调用bgrewriteaof命令,该命令的执行与bgsave有些类似:都是fork子进程进行具体的工作,且都只有在fork时阻塞。
自动触发:通过设置auto-aof-rewrite-min-size选项和auto-aof-rewrite-percentage选项来自动执行BGREWRITEAOF。 只有当auto-aof-rewrite-min-size和auto-aof-rewrite-percentage两个选项同时满足时,才会自动触发AOF重写,即bgrewriteaof操作。
vim /etc/redis/6379.conf
--729--
●auto-aof-rewrite-percentage 100 :当前AOF文件大小(即aof_current_size)是上次日志重写时AOF文件大小(aof_base_size)两倍时,发生BGREWRITEAOF操作
●auto-aof-rewrite-min-size 64mb :当前AOF文件执行BGREWRITEAOF命令的最小值,避免刚开始启动Reids时由于文件尺寸较小导致频繁的BGREWRITEAOF 关于文件重写的流程,有两点需要特别注意:(1)重写由父进程fork子进程进行;(2)重写期间Redis执行的写命令,需要追加到新的AOF文件中,为此Redis引入了aof_rewrite_buf缓存。⑤ 文件重写的流程如下:
(1)Redis父进程首先判断当前是否存在正在执行bgsave/bgrewriteaof的子进程,如果存在则bgrewriteaof命令直接返回,如果存在 bgsave命令则等bgsave执行完成后再执行。
(2)父进程执行fork操作创建子进程,这个过程中父进程是阻塞的。
(3.1)父进程fork后,bgrewriteaof命令返回”Background append only file rewrite started”信息并不再阻塞父进程, 并可以响应其他命令。Redis的所有写命令依然写入AOF缓冲区,并根据appendfsync策略同步到硬盘,保证原有AOF机制的正确。
(3.2)由于fork操作使用写时复制技术,子进程只能共享fork操作时的内存数据。由于父进程依然在响应命令,因此Redis使用AOF重写缓冲区(aof_rewrite_buf)保存这部分数据,防止新AOF文件生成期间丢失这部分数据。也就是说,bgrewriteaof执行期间,Redis的写命令同时追加到aof_buf和aof_rewirte_buf两个缓冲区。
(4)子进程根据内存快照,按照命令合并规则写入到新的AOF文件。
(5.1)子进程写完新的AOF文件后,向父进程发信号,父进程更新统计信息,具体可以通过info persistence查看。
(5.2)父进程把AOF重写缓冲区的数据写入到新的AOF文件,这样就保证了新AOF文件所保存的数据库状态和服务器当前状态一致。
(5.3)使用新的AOF文件替换老文件,完成AOF重写。
3.启动时加载:
当AOF开启时,Redis启动时会优先载入AOF文件来恢复数据;只有当AOF关闭时,才会载入RDB文件恢复数据。
当AOF开启,但AOF文件不存在时,即使RDB文件存在也不会加载。
Redis载入AOF文件时,会对AOF文件进行校验,如果文件损坏,则日志中会打印错误,Redis启动失败。但如果是AOF文件结尾不完整(机器突然宕机等容易导致文件尾部不完整),且aof-load-truncated参数开启,则日志中会输出警告,Redis忽略掉AOF文件的尾部,启动成功。aof-load-truncated参数默认是开启的。
4.AOF的优缺点:
优点:
① AOF的数据完整性比RDB高
② 重写功能会对无效的语句进行删除(目的是为了节省AOF文件占用磁盘空间)
缺点:
① 执行语句一直的情况下,AOF备份的内容更大,RDB备份的内容较小、备份的时结果、语句
② AOF消耗的性能更大,占用磁盘越来越大(相当于mysql的增备)
五、Redis 性能管理:
1.查看Redis内存使用:
info memory
2.内存碎片率:
操作系统分配的内存值 used_memory_rss 除以 Redis 使用的内存总量值 used_memory 计算得出。
内存值 used_memory_rss 表示该进程所占物理内存的大小,即为操作系统分配给 Redis 实例的内存大小。
除了用户定义的数据和内部开销以外,used_memory_rss 指标还包含了内存碎片的开销, 内存碎片是由操作系统低效的分配/回收物理内存导致的(不连续的物理内存分配)。
举例来说:Redis 需要分配连续内存块来存储 1G 的数据集。如果物理内存上没有超过 1G 的连续内存块, 那操作系统就不得不使用多个不连续的小内存块来分配并存储这 1G 数据,该操作就会导致内存碎片的产生。
内存碎片率稍大于1是合理的,这个值表示内存碎片率比较低,也说明 Redis 没有发生内存交换。
内存碎片率超过1.5,说明Redis消耗了实际需要物理内存的150%,其中50%是内存碎片率。需要在redis-cli工具上输入shutdown save 命令,让 Redis 数据库执行保存操作并关闭 Redis 服务,再重启服务器。
内存碎片率低于1的,说明Redis内存分配超出了物理内存,操作系统正在进行内存交换。需要增加可用物理内存或减少 Redis 内存占用。
3.内存使用率:
redis实例的内存使用率超过可用最大内存,操作系统将开始进行内存与swap空间交换。
避免内存交换发生的方法:
针对缓存数据大小选择安装 Redis 实例
尽可能的使用Hash数据结构存储
设置key的过期时间
4.内回收key:
内存清理策略,保证合理分配redis有限的内存资源。
当达到设置的最大阀值时,需选择一种key的回收策略,默认情况下回收策略是禁止删除。
vim /etc/redis/6379.conf
--598--
maxmemory-policy noenviction
volatile-lru:使用LRU算法从已设置过期时间的数据集合中淘汰数据(移除最近最少使用的key,针对设置了TTL的key)
volatile-ttl:从已设置过期时间的数据集合中挑选即将过期的数据淘汰(移除最近过期的key)
volatile-random:从已设置过期时间的数据集合中随机挑选数据淘汰(在设置了TTL的key里随机移除)
allkeys-lru:使用LRU算法从所有数据集合中淘汰数据(移除最少使用的key,针对所有的key)
allkeys-random:从数据集合中任意选择数据淘汰(随机移除key)
noenviction:禁止淘汰数据(不删除直到写满时报错)六、RDB和AOF的总结:
1.RDB和AOF的基本理解:
RDB:周期性地把内存中的数据保存到磁盘中。
AOF:从redis的执行操作日志将执行过程同步到磁盘中。
2.RDB和AOF持久化的过程:
RDB:
写入磁盘中保存的方式: 内存中
写入磁盘中的保存的数据对象:结果数据
内存写入磁盘后,会进行压缩,来减小*rdb的磁盘占用空间量。
AOF:
内存写入到append追加到缓冲区再调用CPU资源来写入到磁盘中
操作日志记录中的执行语句追加到缓冲调用CPU写入磁盘
内存—缓冲—磁盘,写入后,会周期性的进行重写,调过一些"无效操作”保存
3.RDB和AOF的触发方式:
RDB:
手动触发
自动触发:save m n(假设save 900 60,则表示900秒内有60条语句执行,则触发RDB持久化)
特殊触发:当手动关闭Redis时,会进行RDB方式的持久化
/etc/init.d/redis 6379 stop restart
shutdown 关闭时,kill 不会触发
AOF:
手动触发
自动触发
always每条语句,同步执行持久化(有强一致性要的场景)
no 从不进行持久化
every second 每秒进行一次AOE持久化(建议使用的,均衡型场景)
4.RDB和AOE优先级:
因为redis默认是将数据保存在内存中,所以若redis启动、关闭时内存中的数据会丢失
在redis每次启动时,都会读取持久化文件,来会发数据到内存中,以保证reids数据的完整性
RDB和AOF优先级aof>RDB 配置文件可以指定启动 修改各个参数6379.conf
5.RDB和AOF的优缺点:
RDB持久化:
优点:RDB文件紧凑,体积小,网络传输快,适合全量复制;恢复速度比AOF快很多。当然,与AOF相比,RDB最重要的优点之一是对性能的影响相对较小。
缺点:RDB文件的致命缺点在于其数据快照的持久化方式决定了必然做不到实时持久化,而在数据越来越重要的今天,数据的大量丢失很多时候是无法接受的,因此AOF持久化成为主流。此外,RDB文件需要满足特定格式,兼容性差(如老版本的Redis不兼容新版本的RDB文件)。
对于RDB持久化,一方面是bgsave在进行fork操作时Redis主进程会阻塞,另一方面,子进程向硬盘写数据也会带来IO压力。
AOF持久化
优点:与RDB持久化相对应,AOF的优点在于支持秒级持久化、兼容性好,缺点是文件大、恢复速度慢、对性能影响大。
缺点:对于AOF持久化,向硬盘写数据的频率大大提高(everysec策略下为秒级),IO压力更大,甚至可能造成AOF追加阻塞问题。
AOF文件的重写与RDB的bgsave类似,会有fork时的阻塞和子进程的IO压力问题。相对来说,由于AOF向硬盘中写数据的频率更高,因此对 Redis主进程性能的影响会更大。
