纹身网站设计软文广告范文
目录
一、前言
二、核心模版和URP模版
1.区别介绍
2.自己的模版
三、输出节点
1.界面
2.打开OutPut
3.ShderType
4.ShaderName
5.Shader大块内容
6.修改内容
四、预告
一、前言
内容全部基于以下链接基础以上讲的。
Unity | Shader基础知识(什么是shader)_unity shader-CSDN博客
上节课我们简单介绍了一下ASE,这节课讲一下ASE的模版。
为什么要讲模版呢?
如果你会手写shader,你可以不用ASE。
如果你不会手写shader,那你目前只能用模版写。
总结:只要你没学会手写shader,那你就不是自由的,都不能随心所欲的去制作,即使你用了ase,所以还是希望大家重视功底。
有点像AI画图,即使你再擅长和AI交流,只要你不会画画,你就很难得到一个和你心目中一模一样的画。
二、核心模版和URP模版
1.区别介绍
插件是把所有模版写一起的,所以在新建aseShader时,如果建立出来以后是玫红色,就说明这个模版不支持当前管线。
因为群里对URP管线喊得比较多,所以这部分内容均以URP管线为基础制作。
在URP管线中,表面着色器是不支持的,所以,你建表面着色器就会出现玫红色。(如图1、2所示)
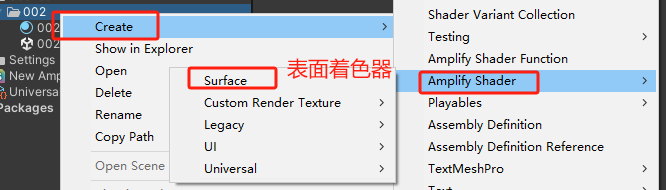
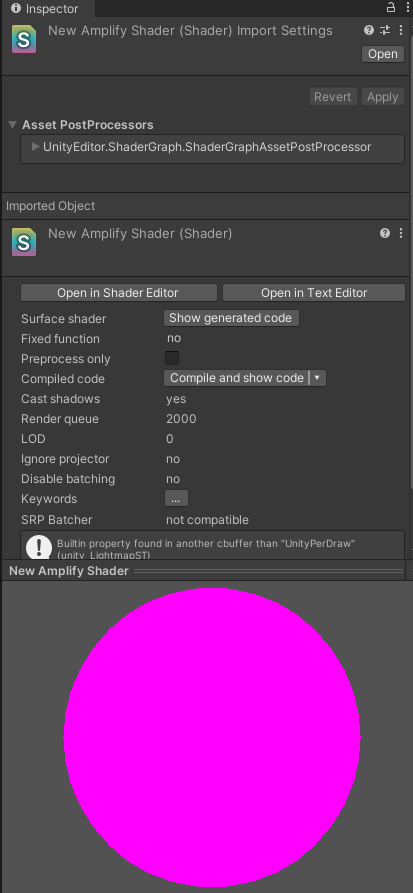
他们互相都有支持和不支持的,所以,自己试吧,也没背下来的必要,用着用着就知道了,所以up这里也不总结了。
如果你学的是核心管线,那大部分教程都会大量使用表面着色器的,因为确实好用。
2.自己的模版
如果你会自己手写,就可以自创。
三、输出节点
在介绍什么是shader的时候,我们讲过,shader是一直在运行的,我们只是抽出来了一部分去改它。
不同的模版意思:人家写好的模版,给了你不同的权限,允许你改不同的地方。
1.界面
你随便创建一个aseShader打开,就可以看见下面的界面。(如图3所示)
2.打开OutPut
左上角有一个OutPutNode(如图4.1所示),内容不一样不要紧,只要标题一致就可以了。
如果没有,点击左上角的方块(如图4.2所示)就有了。
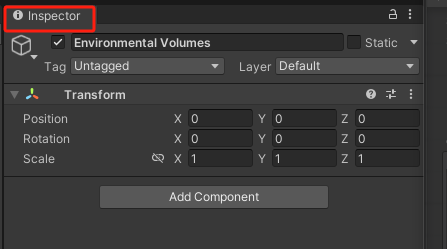
outPut所在的这个窗口的作用,和unity的inspector很像,专门调不同组件参数的。(如图5所示)
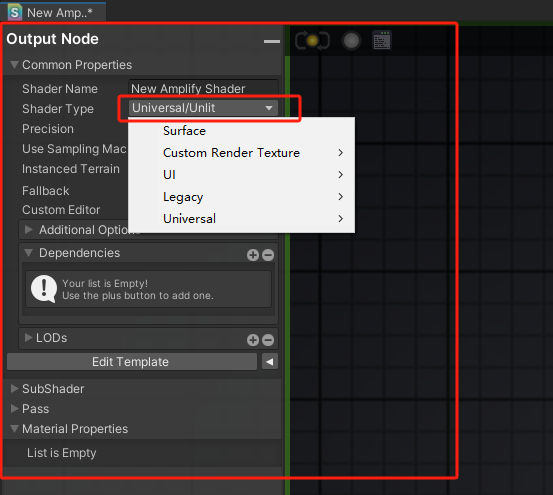
3.ShderType
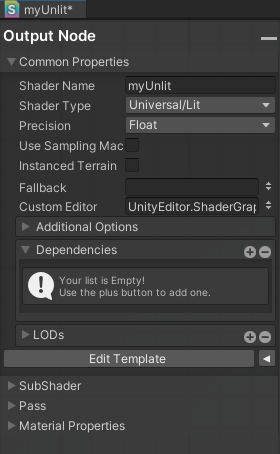
为什么说随便建一个呢?因为里面能改。(如图6所示)
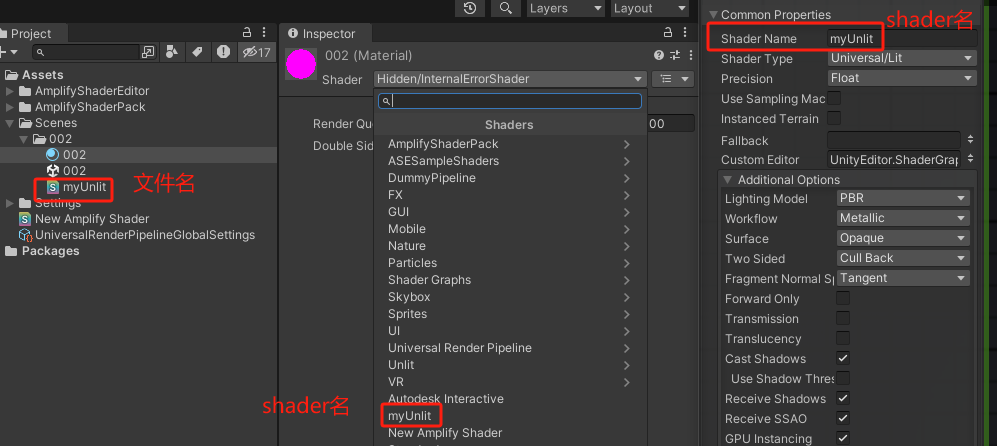
4.ShaderName
如果你仔细看,你会发现,名字里面也能改,但这个改名字是改的shader的名字,外面文件的名字不会改,所以建议二者统一,否则后面容易找不到 。(如图7所示)
5.Shader大块内容
然后我们把OutPut的小三角都收起来。(如图8所示)
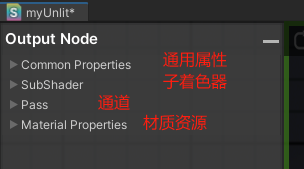
这部分的具体解释,在下方链接
SubShader和Pass:
Unity | Shader基础知识(第二集:shader语言的格式)_unity shader语言-CSDN博客
MaterialProperties:
就是在写Shader时候的properties
Unity | Shader基础知识(第六集:语法<如何加入外部颜色资源>)_unity怎么添加颜色-CSDN博客
看到这里,不知道你能不能感受到, 其实就是写好的模版,让你通过连线调节一下,你能控制的是中间的公式和过程,而不是最底层。
我知道你们着急知道每一条是干什么的,但心急吃不了大胖子,你先别管。
6.修改内容
小三角部分修改的output是总设置,就和unity中的总设置一样,能设置一些东西,但并不是写程序。
同样,我们output中小三角中的也总设置,写材质细节的部分是需要连线的。
那线连在哪呢?
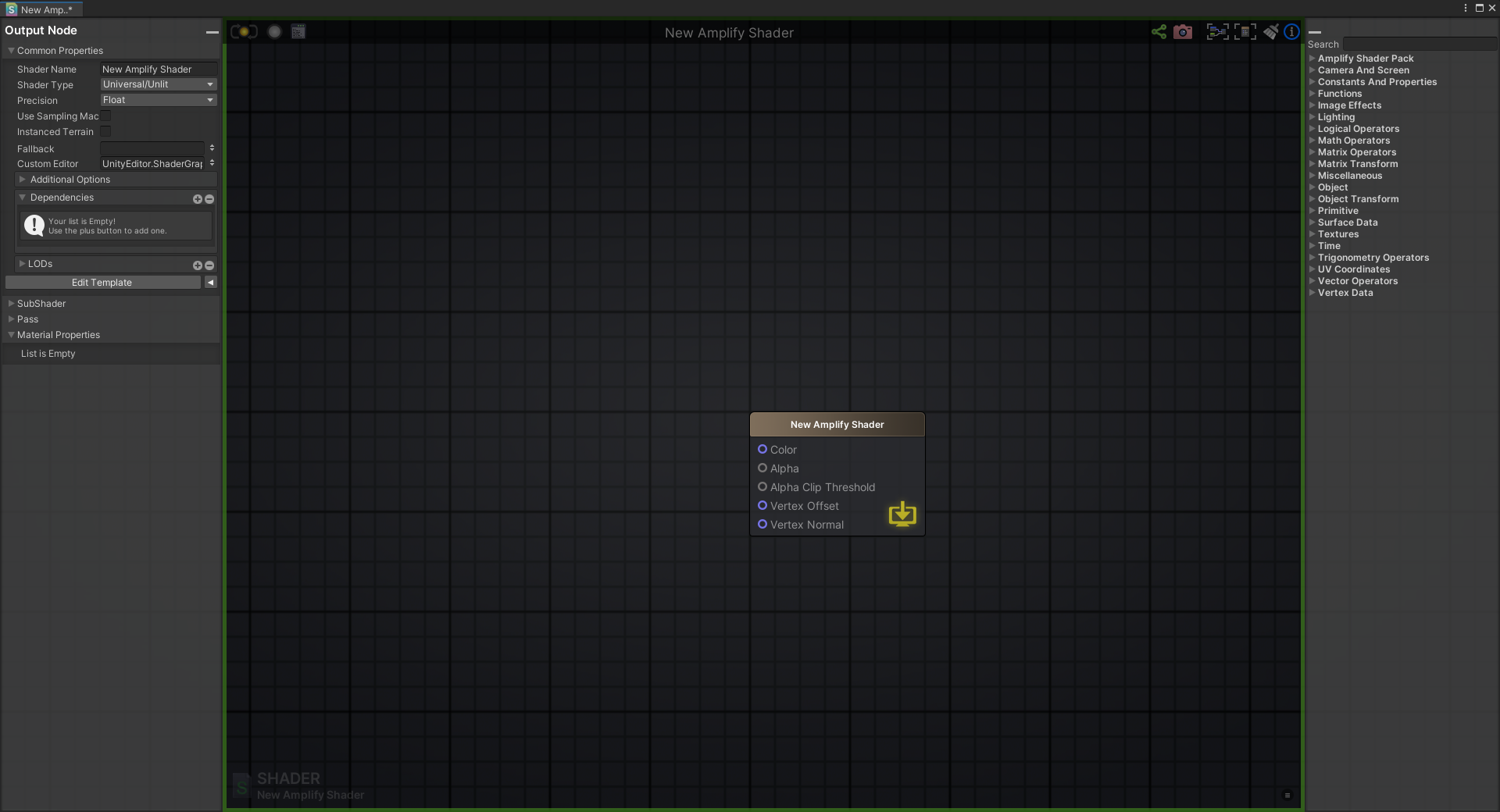
在写好的模版中,它给了你一些能变动的东西。(如图9所示)
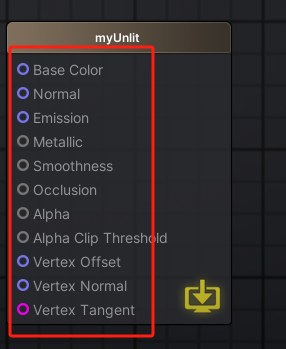
这里面的每一条都是你可以修改的东西,根据你想要的样子去连线修改。每一个模版可以变动的地方不太一样,你们自己可以换换看。
四、预告
下一集我们会讲一个简单的案例,来自己制作属于自己的第一个材质。
