上海企业制作网站有哪些内容星沙网站建设

目录
表的内外连接
一、内连接
二、外连接
1. 左外连接
2. 右外连接
表的内外连接
表的连接分为内连和外连
一、内连接
内连接实际上就是利用where子句对两种表形成的笛卡儿积进行筛选,我们前面博客中的查询都是内连接,也是在开发过程中使用的最多的连接查询。
语法:
select 字段 from 表1 inner join 表2 on 连接条件 and 其他条件;案例:显示SMITH的名字和部门名称
我们依然使用之前的表来进行演示
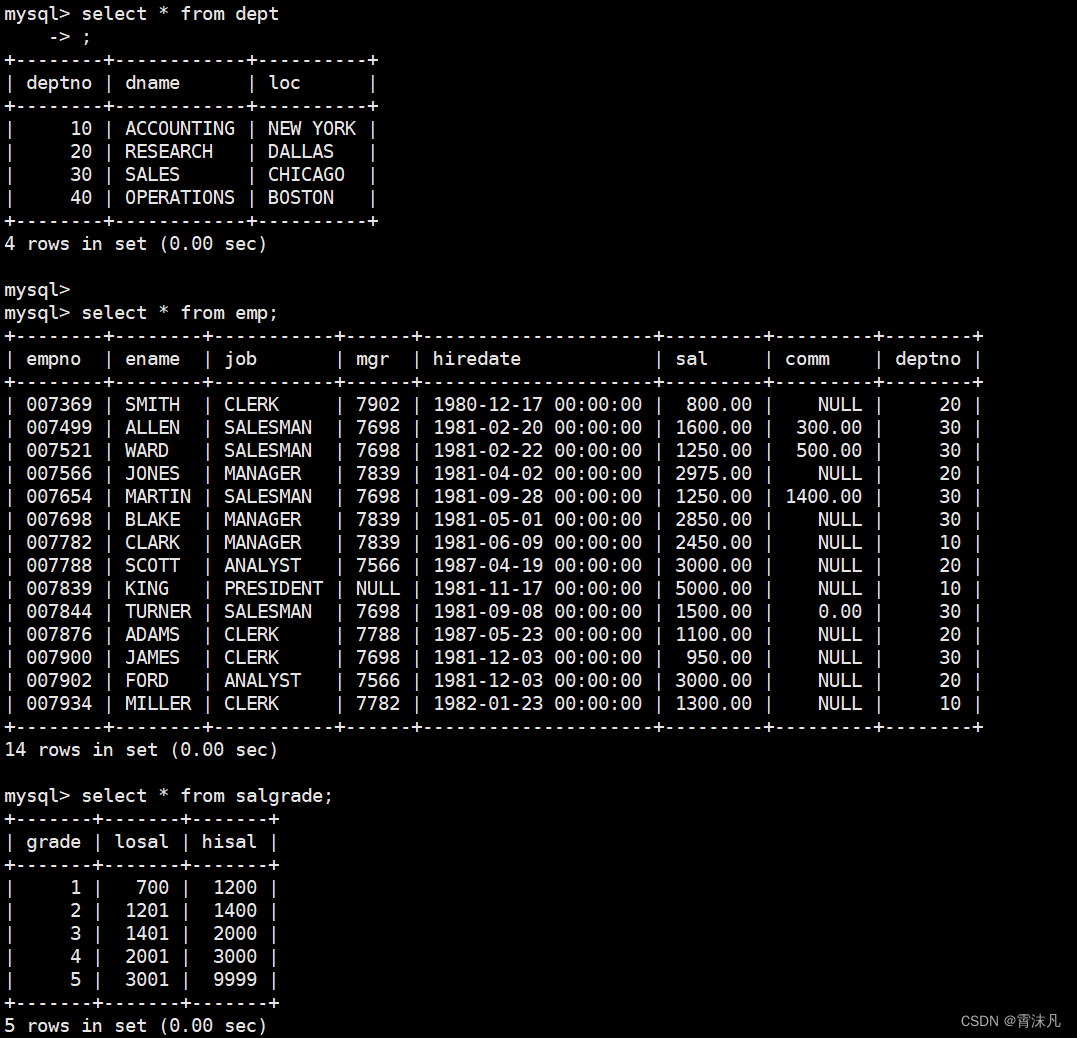
按照我们之前的做法,是将给定题目中所需要的表进行笛卡尔积,然后条件筛选:
select ename, dname from emp, dept where emp.deptno=dept.deptno and ename='SMITH';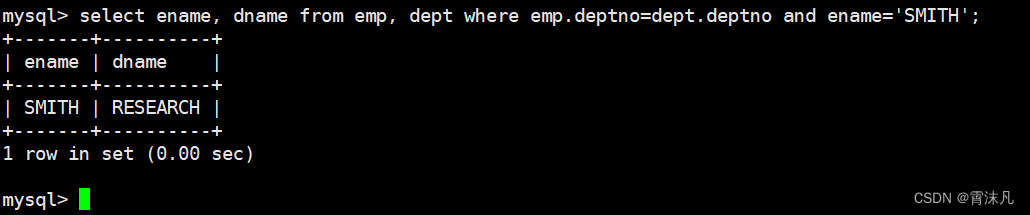
我们也可以使用内连接专门的语法,进行查询:
-- inner join的两侧表明你要将哪两个表进行内连接,on后面就是以什么条件进行内连接
select ename, dname from emp inner join dept on emp.deptno=dept.deptno
and ename='SMITH';
二、外连接
外连接分为左外连接和右外连接
我们先准备两张表,并插入一些数据,连演示左外连接和右外连接:
-- 建两张表
create table stu (id int, name varchar(30)); -- 学生表
insert into stu values(1,'jack'),(2,'tom'),(3,'kity'),(4,'nono');create table exam (id int, grade int); -- 成绩表
insert into exam values(1, 56),(2,76),(11, 8);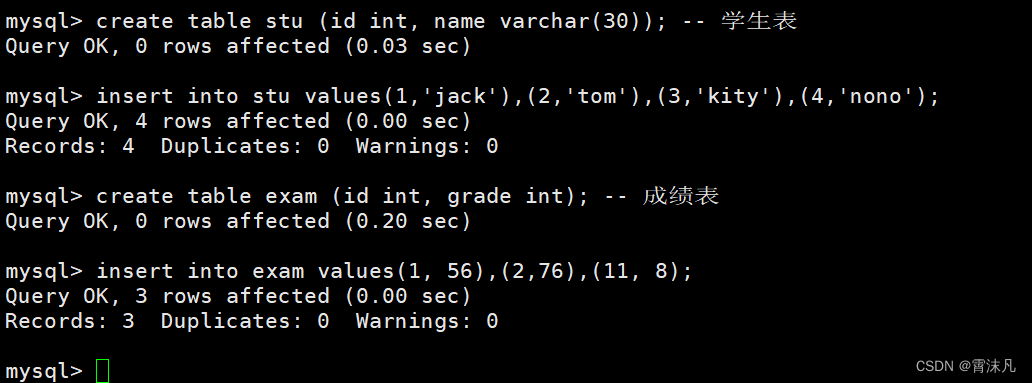
查看两张表:
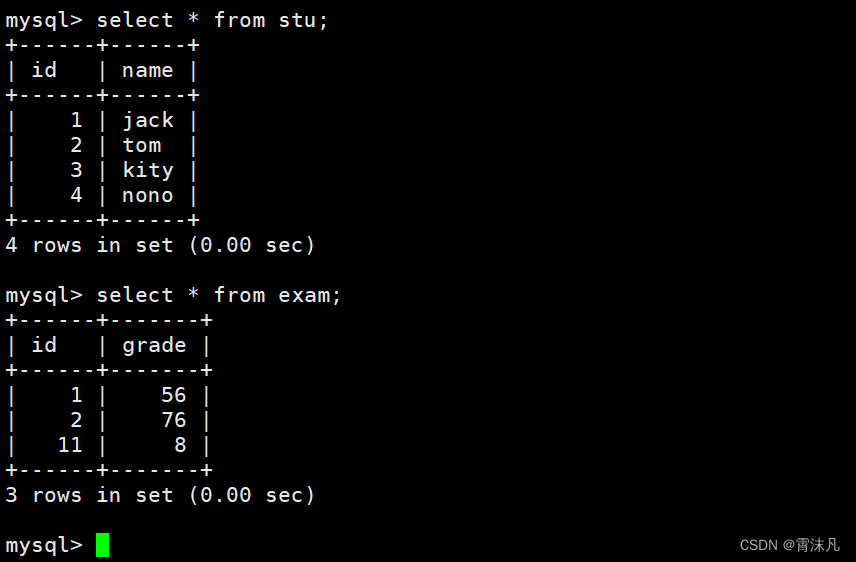
从查询出来的两张表可以看出,stu表中 id为1、2的的学生在exam表中是有相应的成绩的,但是id为4、11的学生要么没有成绩,要么没有名字,这些就属于非法数据,按照我们之前将两张表做笛卡尔积,就是如下的样子:

但有些时候我们想查询数据时,保留这些非法数据,就可以用到左外连接或右外连接
1. 左外连接
如果联合查询,左侧的表完全显示我们就说是左外连接(即左侧的表完全显示,右侧表用空表示)。
语法:
select 字段名 from 表名1 left join 表名2 on 连接条件;案例:查询所有学生的成绩,如果这个学生没有成绩,也要将学生的个人信息显示出来。
select * from stu left join exam on stu.id=exam.id;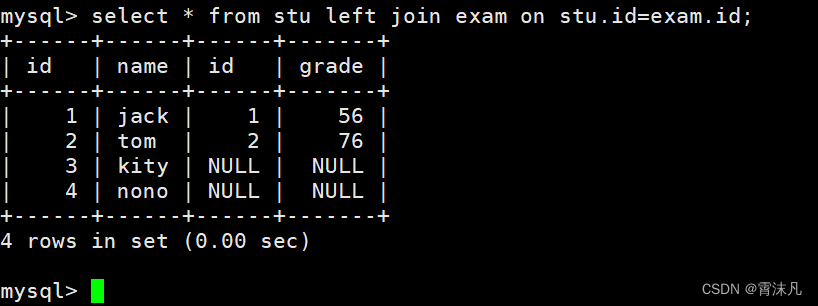
需要注意的是,在使用 A left join B on... 时,A是左表B是右表,左表完全显示指的就是A表。
2. 右外连接
如果联合查询,右侧的表完全显示我们就说是右外连接(即右侧的表完全显示,左侧表用空表示)。
语法:
select 字段 from 表名1 right join 表名2 on 连接条件;案例:对stu表和exam表联合查询,把所有的成绩都显示出来,即使这个成绩没有学生与它对应,也要显示出来。
select * from stu right join exam on stu.id=exam.id;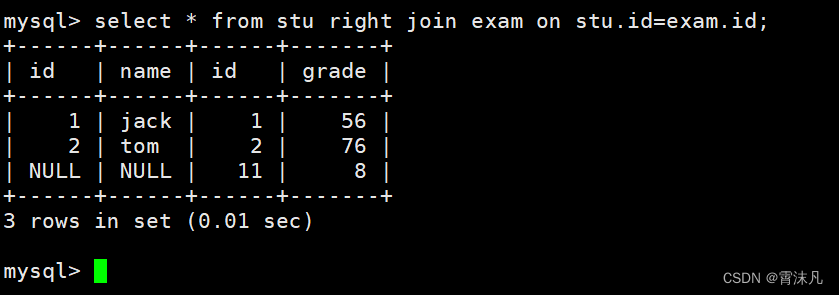
需要注意的是,在使用 A right join B on... 时,A是左表B是右表,右表完全显示指的就是B表。
