wordpress怎么加入站长统计湖州市住房和城乡建设局官方网站
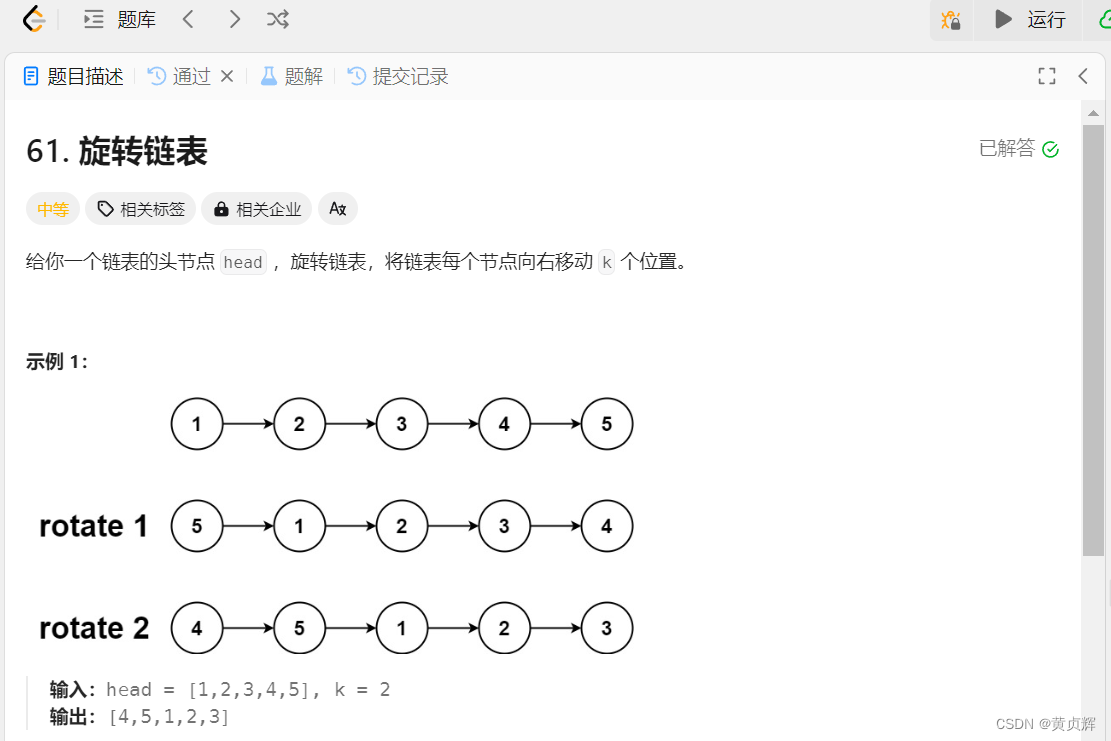
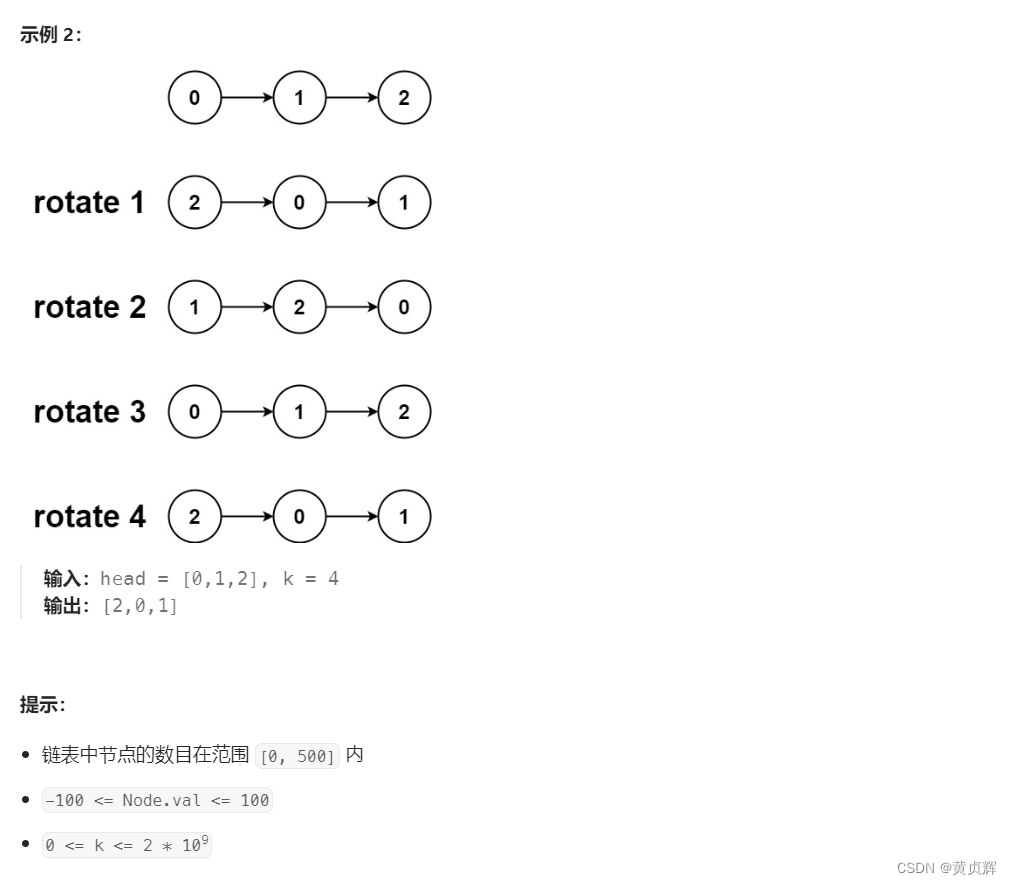
思路:用快慢指针找到最后链表k个需要移动的节点,然后中间断开节点,原尾节点连接原头节点,返回新的节点即可;
但因为k可能比节点数大,所以需要先统计节点个数,再取模,看看k到底需要移动多少个;
class Solution {public ListNode rotateRight(ListNode head, int k) {//只有0或1个节点,直接返回原链表if(head == null || head.next == null) return head;ListNode fast = head;ListNode slow = head;//统计链表有多少个节点,因为k可能会超过节点数,所以需要取模计算;ListNode t = head;int size = 1; //节点数while(t.next!=null) {t = t.next;size++;}if(k%size == 0) return head; //如果k能整除,则不用移动,直接返回k = k%size; //k取 取模后的结果//双指针,slow和fast中间间隔k个节点while(fast.next!=null && k-- > 0) {fast = fast.next;}while(fast.next!=null) {fast = fast.next;slow = slow.next;}ListNode newHead = slow.next;//然后记录下新的头节点slow.next = null;//中间断开fast.next = head;//原尾节点和头节点连接return newHead;//返回新的头节点}
}