四川 网站建设在线设计logo图标
引言
本案例将根据已收集到的电力数据,深度挖掘各电力设备的电流、电压和功率等情况,分析各电力设备的实际用电量,进而为电力公司制定电能能源策略提供一定的参考依据。更多详细内容请参考**《Python数据挖掘:入门进阶与实用案例分析》**一书。

1 案例背景
为了更好地监测用电设备的能耗情况,电力分项计量技术随之诞生。电力分项计量对于电力公司准确预测电力负荷、科学制定电网调度方案、提高电力系统稳定性和可靠性有着重要意义。对用户而言,电力分项计量可以帮助用户了解用电设备的使用情况,提高用户的节能意识,促进科学合理用电。
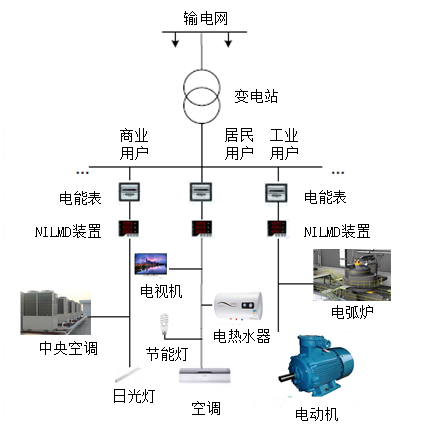
2 分析目标
本案例根据非侵入式负荷检测与分解的电力数据挖掘的背景和业务需求,需要实现的目标如下。
Ø分析每个用电设备的运行属性。
Ø构建设备判别属性库。
Ø利用K最近邻模型,实现从整条线路中“分解”出每个用电设备的独立用电数据。
3 分析过程
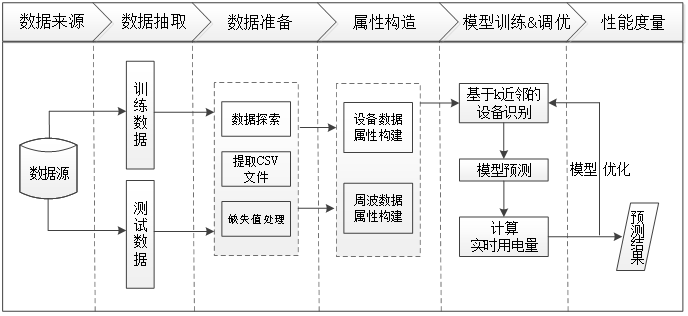
4 数据准备
1.数据探索
在本案例的电力数据挖掘分析中,不会涉及操作记录数据。因此,此处主要获取设备数据、周波数据和谐波数据。在获取数据后,由于数据表较多,每个表的属性也较多,所以需要对数据进行数据探索分析。在数据探索过程中主要根据原始数据特点,对每个设备的不同属性对应的数据进行可视化,得到的部分结果如图1~图3所示。
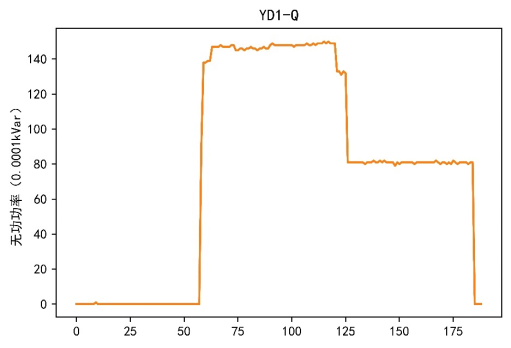
图1 无功功率和总无功功率
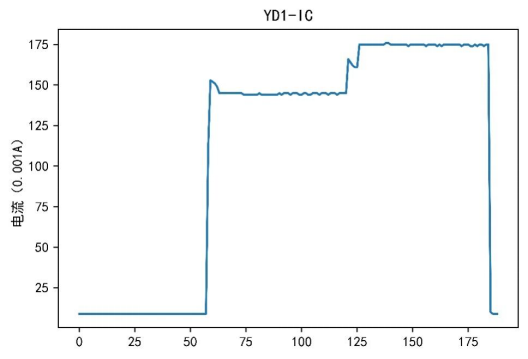
图2 电流轨迹
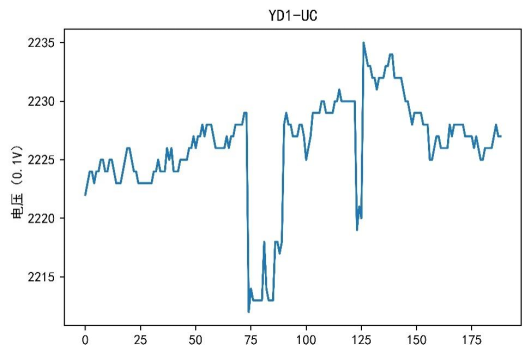
图3 电压轨迹
根据可视化结果可以看出,不同设备之间的电流、电压和功率属性各不相同。
对数据属性进行可视化如代码清单1所示。
代码清单1 对数据属性进行可视化
import pandas as pd import matplotlib.pyplot as plt import os
filename = os.listdir('../data/附件1') # 得到文件夹下的所有文件名称 n_filename = len(filename) # 给各设备的数据添加操作信息,画出各属性轨迹图并保存 def fun(a): save_name = ['YD1', 'YD10', 'YD11', 'YD2', 'YD3', 'YD4', 'YD5', 'YD6', 'YD7', 'YD8', 'YD9'] plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签 plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号 for i in range(a): Sb = pd.read_excel('../data/附件1/' + filename[i], '设备数据', index_col = None) Xb = pd.read_excel('../data/附件1/' + filename[i], '谐波数据', index_col = None) Zb = pd.read_excel('../data/附件1/' + filename[i], '周波数据', index_col = None) # 电流轨迹图 plt.plot(Sb['IC']) plt.title(save_name[i] + '-IC') plt.ylabel('电流(0.001A)') plt.show() # 电压轨迹图 lt.plot(Sb['UC']) plt.title(save_name[i] + '-UC') plt.ylabel('电压(0.1V)') plt.show() # 有功功率和总有功功率 plt.plot(Sb[['PC', 'P']]) plt.title(save_name[i] + '-P') plt.ylabel('有功功率(0.0001kW)') plt.show() # 无功功率和总无功功率 plt.plot(Sb[['QC', 'Q']]) plt.title(save_name[i] + '-Q') plt.ylabel('无功功率(0.0001kVar)') plt.show() # 功率因数和总功率因数 plt.plot(Sb[['PFC', 'PF']]) plt.title(save_name[i] + '-PF') plt.ylabel('功率因数(%)') plt.show() # 谐波电压 plt.plot(Xb.loc[:, 'UC02':].T) plt.title(save_name[i] + '-谐波电压') plt.show() # 周波数据 plt.plot(Zb.loc[:, 'IC001':].T) plt.title(save_name[i] + '-周波数据') plt.show()
fun(n_filename) |
2.缺失值处理
通过数据探索,发现数据中部分“time”属性存在缺失值,需要对这部分缺失值进行处理。由于每份数据中“time”属性的缺失时间段长不同,所以需要进行不同的处理。对于每个设备数据中具有较大缺失时间段的数据进行删除处理,对于具有较小缺失时间段的数据使用前一个值进行插补。
在进行缺失值处理之前,需要将训练数据中所有设备数据中的设备数据表、周波数据表、谐波数据表和操作记录表,以及测试数据中所有设备数据中的设备数据表、周波数据表和谐波数据表都提取出来,作为独立的数据文件,生成的部分文件如图4所示。
图4 提取数据文件部分结果
提取数据文件如代码清单2所示。
代码清单2 提取数据文件
# 将xlsx文件转化为CSV文件 import glob import pandas as pd import math
def file_transform(xls): print('共发现%s个xlsx文件' % len(glob.glob(xls))) print('正在处理............') for file in glob.glob(xls): # 循环读取同文件夹下的xlsx文件 combine1 = pd.read_excel(file, index_col=0, sheet_name=None) for key in combine1: combine1[key].to_csv('../tmp/' + file[8: -5] + key + '.csv', encoding='utf-8') print('处理完成')
xls_list = ['../data/附件1/*.xlsx', '../data/附件2/*.xlsx'] file_transform(xls_list[0]) # 处理训练数据 file_transform(xls_list[1]) # 处理测试数据 |
提取数据文件完成后,对提取的数据文件进行缺失值处理,处理后生成的部分文件如图5所示。
图5 缺失值处理后的部分结果
缺失值处理如代码清单3所示。
代码清单3 缺失值处理
# 对每个数据文件中较大缺失时间点数据进行删除处理,较小缺失时间点数据进行前值替补 def missing_data(evi): print('共发现%s个CSV文件' % len(glob.glob(evi))) for j in glob.glob(evi): fr = pd.read_csv(j, header=0, encoding='gbk') fr['time'] = pd.to_datetime(fr['time']) helper = pd.DataFrame({'time': pd.date_range(fr['time'].min(), fr['time'].max(), freq='S')}) fr = pd.merge(fr, helper, on='time', how='outer').sort_values('time') fr = fr.reset_index(drop=True)
frame = pd.DataFrame() for g in range(0, len(list(fr['time'])) - 1): if math.isnan(fr.iloc[:, 1][g + 1]) and math.isnan(fr.iloc[:, 1][g]): continue else: scop = pd.Series(fr.loc[g]) frame = pd.concat([frame, scop], axis=1) frame = pd.DataFrame(frame.values.T, index=frame.columns, columns=frame.index) frames = frame.fillna(method='ffill') frames.to_csv(j[:-4] + '1.csv', index=False, encoding='utf-8') print('处理完成')
evi_list = ['../tmp/附件1/*数据.csv', '../tmp/附件2/*数据.csv'] missing_data(evi_list[0]) # 处理训练数据 missing_data(evi_list[1]) # 处理测试数据 |
5 属性构造
虽然在数据准备过程中对属性进行了初步处理,但是引入的属性太多,而且这些属性之间存在重复的信息。为了保留重要的属性,建立精确、简单的模型,需要对原始属性进一步筛选与构造。
- 设备数据
在数据探索过程中发现,不同设备的无功功率、总无功功率、有功功率、总有功功率、功率因数和总功率因数差别很大,具有较高的区分度,故本案例选择无功功率、总无功功率、有功功率、总有功功率、功率因数和总功率因数作为设备数据的属性构建判别属性库。
处理好缺失值后,每个设备的数据都由一张表变为了多张表,所以需要将相同类型的数据表合并到一张表中,如将所有设备的设备数据表合并到一张表当中。同时,因为缺失值处理的其中一种方式是使用前一个值进行插补,所以产生了相同的记录,需要对重复出现的记录进行处理,处理后生成的数据表如表1所示。
表1 合并且去重后的设备数据
time | IC | UC | PC | QC | PFC | P | Q | PF | label |
2018/1/27 17:11 | 33 | 2212 | 10 | 65 | 137 | 10 | 65 | 137 | 0 |
2018/1/27 17:11 | 33 | 2212 | 10 | 66 | 143 | 10 | 66 | 143 | 0 |
2018/1/27 17:11 | 33 | 2213 | 10 | 65 | 143 | 10 | 65 | 143 | 0 |
2018/1/27 17:11 | 33 | 2211 | 10 | 66 | 135 | 10 | 66 | 135 | 0 |
2018/1/27 17:11 | 33 | 2211 | 10 | 66 | 141 | 10 | 66 | 141 | 0 |
…… | …… | …… | …… | …… | …… | …… | …… | …… | …… |
合并且去重设备数据如代码清单4所示。
代码清单4 合并且去重设备数据
import glob import pandas as pd import os
# 合并11个设备数据及处理合并中重复的数据 def combined_equipment(csv_name): # 合并 print('共发现%s个CSV文件' % len(glob.glob(csv_name))) print('正在处理............') for i in glob.glob(csv_name): # 循环读取同文件夹下的CSV文件 fr = open(i, 'rb').read() file_path = os.path.split(i) with open(file_path[0] + '/device_combine.csv', 'ab') as f: f.write(fr) print('合并完毕!') # 去重 df = pd.read_csv(file_path[0] + '/device_combine.csv', header=None, encoding='utf-8') datalist = df.drop_duplicates() datalist.to_csv(file_path[0] + '/device_combine.csv', index=False, header=0) print('去重完成')
csv_list = ['../tmp/附件1/*设备数据1.csv', '../tmp/附件2/*设备数据1.csv'] combined_equipment(csv_list[0]) # 处理训练数据 combined_equipment(csv_list[1]) # 处理测试数据 |
- 周波数据
在数据探索过程中发现,周波数据中的电流随着时间的变化有较大的起伏,不同设备的周波数据中的电流绘制出来的折线图的起伏不尽相同,具有明显的差异,故本案例选择波峰和波谷作为周波数据的属性构建判别属性库。
由于原始的周波数据中并未存在电流的波峰和波谷两个属性,所以需要进行属性构建,构建生成的数据表如表2所示。
表2 构建周波数据中的属性生成的数据
波谷 | 波峰 |
344 | 1666365 |
362 | 1666324 |
301 | 1666325 |
314 | 1666392 |
254 | 1666435 |
…… | …… |
构建周波数据中的属性代码如代码清单5所示。
代码清单5 构建周波数据中的属性
# 求取周波数据中电流的波峰和波谷作为属性参数 import glob import pandas as pd from sklearn.cluster import KMeans import os
def cycle(cycle_file): for file in glob.glob(cycle_file): cycle_YD = pd.read_csv(file, header=0, encoding='utf-8') cycle_YD1 = cycle_YD.iloc[:, 0:128] models = [] for types in range(0, len(cycle_YD1)): model = KMeans(n_clusters=2, random_state=10) model.fit(pd.DataFrame(cycle_YD1.iloc[types, 1:])) # 除时间以外的所有列 models.append(model)
# 相同状态间平稳求均值 mean = pd.DataFrame() for model in models: r = pd.DataFrame(model.cluster_centers_, ) # 找出聚类中心 r = r.sort_values(axis=0, ascending=True, by=[0]) mean = pd.concat([mean, r.reset_index(drop=True)], axis=1) mean = pd.DataFrame(mean.values.T, index=mean.columns, columns=mean.index) mean.columns = ['波谷', '波峰'] mean.index = list(cycle_YD['time']) mean.to_csv(file[:-9] + '波谷波峰.csv', index=False, encoding='gbk ')
cycle_file = ['../tmp/附件1/*周波数据1.csv', '../tmp/附件2/*周波数据1.csv'] cycle(cycle_file[0]) # 处理训练数据 cycle(cycle_file[1]) # 处理测试数据
# 合并周波的波峰波谷文件 def merge_cycle(cycles_file): means = pd.DataFrame() for files in glob.glob(cycles_file): mean0 = pd.read_csv(files, header=0, encoding='gbk') means = pd.concat([means, mean0]) file_path = os.path.split(glob.glob(cycles_file)[0]) means.to_csv(file_path[0] + '/zuhe.csv', index=False, encoding='gbk') print('合并完成')
cycles_file = ['../tmp/附件1/*波谷波峰.csv', '../tmp/附件2/*波谷波峰.csv'] merge_cycle(cycles_file[0]) # 训练数据 merge_cycle(cycles_file[1]) # 测试数据 |
6 模型训练
在判别设备种类时,选择K最近邻模型进行判别,利用属性构建而成的属性库训练模型,然后利用训练好的模型对设备1和设备2进行判别。构建判别模型并对设备种类进行判别,如代码清单6所示。
代码清单6 建立判别模型并对设备种类进行判别
import glob import pandas as pd from sklearn import neighbors import pickle import os
# 模型训练 def model(test_files, test_devices): # 训练集 zuhe = pd.read_csv('../tmp/附件1/zuhe.csv', header=0, encoding='gbk') device_combine = pd.read_csv('../tmp/附件1/device_combine.csv', header=0, encoding='gbk') train = pd.concat([zuhe, device_combine], axis=1) train.index = train['time'].tolist() # 把“time”列设为索引 train = train.drop(['PC', 'QC', 'PFC', 'time'], axis=1) train.to_csv('../tmp/' + 'train.csv', index=False, encoding='gbk') # 测试集 for test_file, test_device in zip(test_files, test_devices): test_bofeng = pd.read_csv(test_file, header=0, encoding='gbk') test_devi = pd.read_csv(test_device, header=0, encoding='gbk') test = pd.concat([test_bofeng, test_devi], axis=1) test.index = test['time'].tolist() # 把“time”列设为索引 test = test.drop(['PC', 'QC', 'PFC', 'time'], axis=1)
# K最近邻 clf = neighbors.KNeighborsClassifier(n_neighbors=6, algorithm='auto') clf.fit(train.drop(['label'], axis=1), train['label']) predicted = clf.predict(test.drop(['label'], axis=1)) predicted = pd.DataFrame(predicted) file_path = os.path.split(test_file)[1] test.to_csv('../tmp/' + file_path[:3] + 'test.csv', encoding='gbk') predicted.to_csv('../tmp/' + file_path[:3] + 'predicted.csv', index=False, encoding='gbk') with open('../tmp/' + file_path[:3] + 'model.pkl', 'ab') as pickle_file: pickle.dump(clf, pickle_file) print(clf)
model(glob.glob('../tmp/附件2/*波谷波峰.csv'), glob.glob('../tmp/附件2/*设备数据1.csv')) |
7 性能度量
根据代码清单6的设备判别结果,对模型进行模型评估,得到的结果如下,混淆矩阵如图7所示,ROC曲线如图8所示 。
模型分类准确度: 0.7951219512195122模型评估报告:precision recall f1-score support0.0 1.00 0.84 0.92 6421.0 0.00 0.00 0.00 061.0 0.00 0.00 0.00 091.0 0.78 0.84 0.81 7792.0 0.00 0.00 0.00 593.0 0.76 0.75 0.75 59111.0 0.00 0.00 0.00 0accuracy 0.80 205macro avg 0.36 0.35 0.35 205weighted avg 0.82 0.80 0.81 205计算auc:0.8682926829268293
注:此处部分结果已省略。
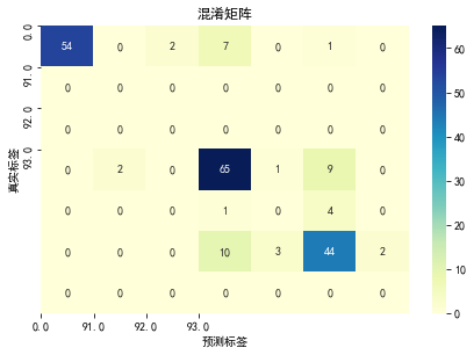
图7 混淆矩阵
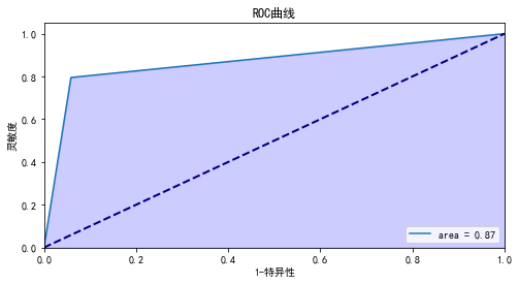
图8 ROC曲线
模型评估如代码清单7所示。
代码清单7 模型评估
import globimport pandas as pdimport matplotlib.pyplot as pltimport seaborn as snsfrom sklearn import metricsfrom sklearn.preprocessing import label_binarizeimport osimport pickle# 模型评估def model_evaluation(model_file, test_csv, predicted_csv):for clf, test, predicted in zip(model_file, test_csv, predicted_csv):with open(clf, 'rb') as pickle_file:clf = pickle.load(pickle_file)test = pd.read_csv(test, header=0, encoding='gbk')predicted = pd.read_csv(predicted, header=0, encoding='gbk')test.columns = ['time', '波谷', '波峰', 'IC', 'UC', 'P', 'Q', 'PF', 'label']print('模型分类准确度:', clf.score(test.drop(['label', 'time'], axis=1), test['label']))print('模型评估报告:\n', metrics.classification_report(test['label'], predicted))confusion_matrix0 = metrics.confusion_matrix(test['label'], predicted)confusion_matrix = pd.DataFrame(confusion_matrix0)class_names = list(set(test['label']))tick_marks = range(len(class_names))sns.heatmap(confusion_matrix, annot=True, cmap='YlGnBu', fmt='g')plt.xticks(tick_marks, class_names)plt.yticks(tick_marks, class_names)plt.tight_layout()plt.title('混淆矩阵')plt.ylabel('真实标签')plt.xlabel('预测标签')plt.show()y_binarize = label_binarize(test['label'], classes=class_names)predicted = label_binarize(predicted, classes=class_names)fpr, tpr, thresholds = metrics.roc_curve(y_binarize.ravel(), predicted.ravel())auc = metrics.auc(fpr, tpr)print('计算auc:', auc) # 绘图plt.figure(figsize=(8, 4))lw = 2plt.plot(fpr, tpr, label='area = %0.2f' % auc)plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')plt.fill_between(fpr, tpr, alpha=0.2, color='b')plt.xlim([0.0, 1.0])plt.ylim([0.0, 1.05])plt.xlabel('1-特异性')plt.ylabel('灵敏度')plt.title('ROC曲线')plt.legend(loc='lower right')plt.show()model_evaluation(glob.glob('../tmp/*model.pkl'),glob.glob('../tmp/*test.csv'),glob.glob('../tmp/*predicted.csv'))
根据分析目标,需要计算实时用电量。实时用电量计算的是瞬时的用电器的电流、电压和时间的乘积,公式如下。
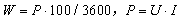
其中,为实时用电量,单位是0.001kWh。为功率,单位为W。
实时用电量计算,得到的实时用电量如表3所示。
表3 实时用电量

计算实时用电量如代码清单8所示。
代码清单8 计算实时用电量
# 计算实时用电量并输出状态表def cw(test_csv, predicted_csv, test_devices):for test, predicted, test_device in zip(test_csv, predicted_csv, test_devices):# 划分预测出的时刻表test = pd.read_csv(test, header=0, encoding='gbk')test.columns = ['time', '波谷', '波峰', 'IC', 'UC', 'P', 'Q', 'PF', 'label']test['time'] = pd.to_datetime(test['time'])test.index = test['time']predicteds = pd.read_csv(predicted, header=0, encoding='gbk')predicteds.columns = ['label']indexes = []class_names = list(set(test['label']))for j in class_names:index = list(predicteds.index[predicteds['label'] == j])indexes.append(index)# 取出首位序号及时间点from itertools import groupby # 连续数字dif_indexs = []time_indexes = []info_lists = pd.DataFrame()for y, z in zip(indexes, class_names):dif_index = []fun = lambda x: x[1] - x[0]for k, g in groupby(enumerate(y), fun):dif_list = [j for i, j in g] # 连续数字的列表if len(dif_list) > 1:scop = min(dif_list) # 选取连续数字范围中的第一个else:scop = dif_list[0 ]dif_index.append(scop)time_index = list(test.iloc[dif_index, :].index)time_indexes.append(time_index)info_list = pd.DataFrame({'时间': time_index, 'model_设备状态': [z] * len(time_index)})dif_indexs.append(dif_index)info_lists = pd.concat([info_lists, info_list])# 计算实时用电量并保存状态表test_devi = pd.read_csv(test_device, header=0, encoding='gbk')test_devi['time'] = pd.to_datetime(test_devi['time'])test_devi['实时用电量'] = test_devi['P'] * 100 / 3600info_lists = info_lists.merge(test_devi[['time', '实时用电量']],how='inner', left_on='时间', right_on='time')info_lists = info_lists.sort_values(by=['时间'], ascending=True)info_lists = info_lists.drop(['time'], axis=1)file_path = os.path.split(test_device)[1]info_lists.to_csv('../tmp/' + file_path[:3] + '状态表.csv', index=False, encoding='gbk')print(info_lists)cw(glob.glob('../tmp/*test.csv'),glob.glob('../tmp/*predicted.csv'),glob.glob('../tmp/附件2/*设备数据1.csv'))
8 推荐阅读

正版链接:https://item.jd.com/13814157.html
**《Python数据挖掘:入门、进阶与实用案例分析》**是一本以项目实战案例为驱动的数据挖掘著作,它能帮助完全没有Python编程基础和数据挖掘基础的读者快速掌握Python数据挖掘的技术、流程与方法。在写作方式上,与传统的“理论与实践结合”的入门书不同,它以数据挖掘领域的知名赛事“泰迪杯”数据挖掘挑战赛(已举办10届)和“泰迪杯”数据分析技能赛(已举办5届)(累计1500余所高校的10余万师生参赛)为依托,精选了11个经典赛题,将Python编程知识、数据挖掘知识和行业知识三者融合,让读者在实践中快速掌握电商、教育、交通、传媒、电力、旅游、制造等7大行业的数据挖掘方法。
本书不仅适用于零基础的读者自学,还适用于教师教学,为了帮助读者更加高效地掌握本书的内容,本书提供了以下10项附加价值:
(1)建模平台:提供一站式大数据挖掘建模平台,免配置,包含大量案例工程,边练边学,告别纸上谈兵
(2)视频讲解:提供不少于600分钟Python编程和数据挖掘相关教学视频,边看边学,快速收获经验值
(3)精选习题:精心挑选不少于60道数据挖掘练习题,并提供详细解答,边学边练,检查知识盲区
(4)作者答疑:学习过程中有任何问题,通过“树洞”小程序,纸书拍照,一键发给作者,边问边学,事半功倍
**(5)数据文件:**提供各个案例配套的数据文件,与工程实践结合,开箱即用,增强实操性
**(6)程序代码:**提供书中代码的电子文件及相关工具的安装包,代码导入平台即可运行,学习效果立竿见影
**(7)教学课件:**提供配套的PPT课件,使用本书作为教材的老师可以申请,节省备课时间
**(8)模型服务:**提供不少于10个数据挖掘模型,模型提供完整的案例实现过程,助力提升数据挖掘实践能力
**(9)教学平台:**泰迪科技为本书提供的附加资源提供一站式数据化教学平台,附有详细操作指南,边看边学边练,节省时间
**(10)就业推荐:**提供大量就业推荐机会,与1500+企业合作,包含华为、京东、美的等知名企业
通过学习本书,读者可以理解数据挖掘的原理,迅速掌握大数据技术的相关操作,为后续数据分析、数据挖掘、深度学习的实践及竞赛打下良好的技术基础。

9 参与方式
- 本次送书2本
- 活动时间:截止到2023-11-2
- 参与方式:关注博主、点赞、收藏并任意评论
PS:评论字数20字以上,根据评论的点赞数量靠前的抽取 - 阅读量过2k加一本 (最终送出的书 根据阅读量送出 如果阅读量不达标就按实际的送)
PS:获奖名单活动结束后 粉丝群和 评论区公布
